模糊控制：MATLAB实现

基于模糊理论的广西城市的分类

利用MATLAB的模糊聚类分析实现城市分类的智能计算

文章简介：利用MATLAB的模糊聚类分析实现城市分类的智能计算，使用到了模糊控制算法，有兴趣的友友可以看看。都是一些比较基础的代码。

一、研究背景

城市分类，根据城市职能、城市规模、城市形态等方面的差异对城市进行的类分。城市之间的差异反映在人口规模与结构、产业结构、城市形态，生活方式和生活水平、地理位置及历史沿革等诸多方面。城市的分类，因不同的目的和要求，选用上述一个或几个指标进行而有所区别，体现城市性质的职能分类，根据人口数量而作的规模分类、反映城市外貌的形态分类，以及按照地理、交通位置或历史起源把城市分成不同类型。其中城市职能分类和规模分类最能揭示城市的基本特征，因而受到广泛的重视。

二、研究目的

通过掌握数据文件的标准化、模糊相似矩阵的建立方法、学会传递闭包矩阵的求解方法；使用MATLAB软件进行模糊矩阵的编程运算和仿真，实现模糊聚类分析；对广西的城区面积和城区人口数据进行城市分类，将广西21座城市进行划分，有助于完善城市城区面积和城区人口的分类系统；这有助于挖掘城市发展的规律与特点，深化城市发展的理论研究；同时有助于决策者在面临城市发展规划作出最优决策，从而能更好的对广西城市发展做更好的规划。因此，在广西城市发展战略的大背景下有很强的理论和现实意义。

三、研究内容

1、根据下面表格中的数据，用Matlab编程进行数据标准化处理；

2、根据标准化处理后的数据，用Matlab编程，建立模糊相似矩阵，并编程求出其传递闭包矩阵；

3、建立模糊等价矩阵，根据原始数据，对广西城市进行分类并分析

四、方法步骤

1. 将表《2017年全国城市人口和建设用地》中广西壮族自治区21所城市的城区人口和城区面积数据导入MATLAB软件；

程序见附录1：

1. 读取数据的高和宽，建立原始矩阵A，对原始矩阵A应用极差正规化方法进行数据规格化，得到数据矩阵。

程序见附录2：

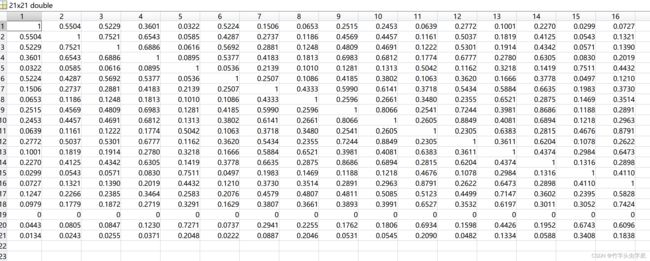
1. 对数据矩阵应用最小最大法得到模糊相似矩阵。

程序见附录3：

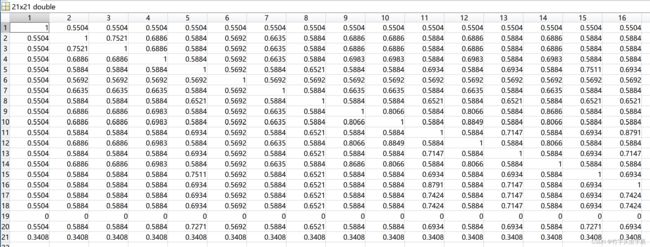
1. 应用传递闭包方法将模糊相似矩阵转化为模糊等价矩阵。

程序见附录4：

1. 建立λ-截矩阵，按照λ有大到小进行聚类分析。

程序见附录5：

五、结果和分析

1. 运行代码

为了便于看到所有的结果，先将显示截距阵的一行代码注释掉，运行得到所有分类结果如下图

1. 选取合适的λ值

当我们选取λ=0.6521时函数得到的截距阵及进行的分类结果图如下

   

分类结果为：

第1类：x19

第2类：x21

第3类：x6

第4类：x5 x8 x11 x13 x15 x16 x17 x18 x20

第5类：x2 x3 x4 x7 x9 x10 x12 x14

第6类：x1

1. 城市分类

根据以上数据，我们根据城市的城区面积和城区人口数据将广西城市分成6大类，取λ=0.6521。此时，广西的城市分类为：

第一类城市：南宁

第二类城市：北海

第三类城市： 柳州  桂林 梧州 防城港 钦州  贵港  玉林 百色

第四类城市：岑溪 桂平 北流 靖西 贺州 河池 来宾 崇左

第五类城市：凭祥

第六类城市：合山

1. 数据分析

我们根据原始数据将关系城市划分为人口密集的大型城市、非人口密集的大型城市、人口适中的中型城市、人口适中的小型城市、人口较少的小型城市、人口较少的超小型城市。

由上述可知广西城市大部分为第三类人口适中的中型城市和第四类人口适中的小型城。

第一类城市南宁城区面积大且城区人口多，为人口密集的大型城市，在广西城市发展中处于领先地位。

第二类城市北海城区面积最大但城区人口相对于南宁而言较少，属于非人口密集的大型城市，说明北海正在快速发展中，有望发展成人口密集的大型城市。

第三类城市中桂林的城区面积最大，柳州的城区人口最多，平均城区面积为394.78平方公里，平均城区人口53.9万人；柳州、桂林、梧州、防城港、钦州、贵港、玉林、百色均属于人口适中的中型城市，一共8个城市，是当前广西城市发展的主力。

第四类城市中北流的城区面积最大，河池的城区人口最多，平均城区面积为83.23平方公里；平均城区人口20.57万人；岑溪、桂平、北流、靖西、贺州、河池、来宾、崇左均属于人口适中的小型城市，一共9个城市是广西城市发展的后备军。

第五类城市凭祥和第六类城市均因为城区面积小或城区人口少，分别属于人口较少的小型城市和人口较少的超小型城市。

代码附录1：

A=xlsread('D:\Users\74744\Desktop\GX1.xlsx');

代码附录2：

[hei,wid]=size(A);

n=zeros(hei,wid);

for i=1:hei

    for j=1:wid

        n(i,j)=(A(i,j)-min(A(:,j)))/(max(A(:,j))-min(A(:,j)));

    end

end 

   

附录3：

[hei,wid]=size(n);

m=zeros(hei,hei);

for i=1:hei

    for j=1:hei

        maxnum=0;

        minnum=0;

        for k=1:wid

            maxnum=maxnum+max(n(i,k),n(j,k));

            minnum=minnum+min(n(i,k),n(j,k));

        end

        m(i,j)=minnum/maxnum;

    end

end 

附录4：

[hei,wid]=size(m);

ab=zeros(hei,wid);

flag=0;

while(flag==0)

    m1=size(m,1);

    n1=size(m,2);

    for i=1:m1

        for j=1:n1

            ab(i,j)=max(min([m(i,:);m(:,j)']));

        end

    end

    if(ab==m)

        flag=1;

    else

       m=ab;

    end

end

附录5：

L=unique(m)';

    a1=size(m);

    D=zeros(a1);

     for m2=length(L):-1:1

        k=L(m2);

        for i=1:a1

            for j=1:a1

                if m(i,j)>=k

                    D(i,j)=1;

                else

                    D(i,j)=0;

                end

            end

        end

 B=unique(D,'rows');

    [hei]=size(B);

 for j=1:hei

     eval(['L',num2str(j) '= [];'])

 end

 for i=a1:-1:1

     for j=1:hei

         if D(i,:)==B(j,:)

             p=eval(['L',num2str(j);]);

             p=[['x',num2str(i),' '] p];

             eval([ 'L',num2str(j) '=p;']);

         end

     end

 end

fprintf("当分类系数k=%5.4f时，",L(m2));

 fprintf("所得截矩阵为:\n\n");

 %disp(D);

 fprintf("分类结果为：\n");

 for j=1:hei

     

     fprintf("第%d类：",j);

     %['L',num2str(j);]

     disp(eval(['L',num2str(j);]));

 end

 fprintf("\n");

 end