代码随想录算法学习心得 17 | 654.最大二叉树、617.合并二叉树、700.二叉树搜索树中的搜索、98.验证二叉搜索树...

一、最大二叉树

链接：力扣

描述：给定一个不重复的整数数组 nums 。 最大二叉树 可以用下面的算法从 nums 递归地构建:

    创建一个根节点，其值为 nums 中的最大值。
    递归地在最大值 左边 的 子数组前缀上 构建左子树。
    递归地在最大值 右边 的 子数组后缀上 构建右子树。

 

---

思路：先进行排序，找到最大值及其位置，在对原来的数组进行分割，递归调用即可。

---

代码如下：

#include 
#include 
#include 
using namespace std;
struct TreeNode {
    int val;
    TreeNode* left;
    TreeNode* right;
    TreeNode() : val(0), left(nullptr), right(nullptr) {}
    TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
    TreeNode(int x, TreeNode* left, TreeNode* right) : val(x), left(left), right(right) {}

};
class Solution 
{
public:
    TreeNode* constructMaximumBinaryTree(vector& nums) 
    {
        vectortemp(nums.begin(), nums.end());
        sort(temp.begin(), temp.end());
        if (nums.size() == 0)
        {
            return NULL;
        }
        //易错，数组容易超范围
        TreeNode* root = new TreeNode(temp[temp.size() - 1]);
        int max_index;
        for (max_index= 0; max_index < nums.size(); max_index++)
        {
            if (nums[max_index] == temp[temp.size() - 1])
            {
                break;
            }
        }
        vectorleft(nums.begin(), nums.begin() + max_index);
        vectorright(nums.begin() + max_index + 1, nums.end());
        root->left=constructMaximumBinaryTree(left);
        root->right=constructMaximumBinaryTree(right);
        return root;
    }
};


int main()
{
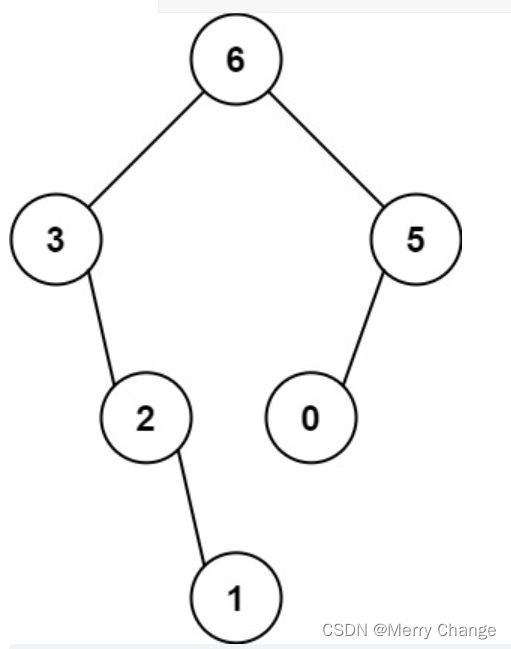
    vectorv{ 3,2,1,6,0,5 };
    Solution s;
    s.constructMaximumBinaryTree(v);
    return 0;
}

运行如下：

---

二、合并二叉树

链接：力扣

描述：给你两棵二叉树： root1 和 root2 。

想象一下，当你将其中一棵覆盖到另一棵之上时，两棵树上的一些节点将会重叠（而另一些不会）。你需要将这两棵树合并成一棵新二叉树。合并的规则是：如果两个节点重叠，那么将这两个节点的值相加作为合并后节点的新值；否则，不为 null 的节点将直接作为新二叉树的节点。

返回合并后的二叉树。

注意: 合并过程必须从两个树的根节点开始。

---

思路：使用前序遍历递归调用，两棵树同步进行，按照合并规则来，如果两个节点重叠，那么将这两个节点的值相加作为合并后节点的新值；否则，不为 null 的节点将直接作为新二叉树的节点。

---

代码如下：

#include 
#include 
#include 
using namespace std;
struct TreeNode {
    int val;
    TreeNode* left;
    TreeNode* right;
    TreeNode() : val(0), left(nullptr), right(nullptr) {}
    TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
    TreeNode(int x, TreeNode* left, TreeNode* right) : val(x), left(left), right(right) {}

};
class Solution {
public:
    TreeNode* mergeTrees(TreeNode* root1, TreeNode* root2) 
    {
        //递归，前序遍历：中左右
        //包含了root1和root2都为空的情况
        if (root1 == NULL)
        {
            return root2;
        }
        else if (root2 == NULL)
        {
            return root1;
        }
        //重新定义一个新的二叉树
        TreeNode* root = new TreeNode(root1->val + root2->val);
        root->left = mergeTrees(root1->left, root2->left);
        root->right = mergeTrees(root1->right, root2->right);
        return root;
    }
};

运行如下：

---

三、二叉搜索树中的搜索

链接：力扣

描述：给定二叉搜索树（BST）的根节点 root 和一个整数值 val。

你需要在 BST 中找到节点值等于 val 的节点。 返回以该节点为根的子树。 如果节点不存在，则返回 null 。

---

思路：1、用递归来进行处理。

2、层序遍历

---

递归代码如下：

TreeNode* searchBST(TreeNode* root, int val)
    {
        //递归
        if (!root)
        {
            return NULL;
        }
        if (root->val == val)
        {
            return root;
        }
        TreeNode* left=searchBST(root->left,val);
        if (left)
        {
            return left;
        }
        TreeNode* right =searchBST(root->right,val);
        if (right)
        {
            return right;
        }
        return NULL;
    }

---

迭代的代码如下：

TreeNode* searchBST(TreeNode* root, int val)
    {
        queueq;//辅助队列
        TreeNode* result=NULL;
        q.push(root);
        while (!q.empty())
        {
            int size = q.size();
            while (size--)
            {
                TreeNode* node = q.front();
                q.pop();
                if (node->val == val)
                {
                    result = node;
                    break;
                }
                if (node->left)
                {
                    q.push(node->left);
                }
                if (node->right)
                {
                    q.push(node->right);
                }
            }
        }
        return result;
    }

运行如下：

---

四、验证二叉搜索树

链接：力扣

描述：给你一个二叉树的根节点 root ，判断其是否是一个有效的二叉搜索树。

有效 二叉搜索树定义如下：

    节点的左子树只包含 小于 当前节点的数。
    节点的右子树只包含 大于 当前节点的数。
    所有左子树和右子树自身必须也是二叉搜索树。

---

思路：注意是左边的结点全都比中结点小，而不是某个子树上满足即可。空结点也是二叉搜索树。

1、可先中序遍历得到中序遍历的结果，再判断是否是递增的。

2、用中序遍历。可以设一个全局变量记录每一次遍历的最大值，由于题目最小值可以取int的最小值，所以要定义longlong型变量，如果哪一次没有更新，则说明非递增顺序，返回false

---

第一种方法代码如下：

lic:
    void inorder_traversal(vector& result,TreeNode *cur)
    {
        inorder_traversal(result,cur->left);
        result.push_back(cur->val);
        inorder_traversal(result,cur->right);
    }
    bool isValidBST(TreeNode* root) 
    {
        //用数组来放中序遍历的结果
        if (root == NULL)
        {
            return true;
        }
        vectorinorder;
        this->inorder_traversal(inorder, root);
        //判断是否递增,i < inorder.size()-1易错
        for (int i = 0; i < inorder.size()-1; i++)
        {
            if (inorder[i] >= inorder[i + 1])
            {
                return false;
            }
        }
        return true;
    }

第二种方法代码如下：

long long max_value = LONG_MIN;//易错，必须是全局变量
    bool isValidBST(TreeNode* root)
    {
        //直接比较两个树节点的大小
        //用中序遍历
        if (!root)
        {
            //空节点也是二叉搜索平衡树
            return true;
        }
        bool left=isValidBST(root->left);
        
        if (max_value < root->val)
        {
            max_value = root->val;
        }
        else
        {
            return false;
        }
        bool right=isValidBST(root->right);
        return left && right;
    }

运行如下：