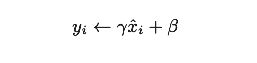深度学习入门之5--网络学习相关技巧3(Batch Normalization)

目录

1、Batch Normalization算法

2、评估

2.1、common/multi_layer_net_extend.py

2.2、batch_norm_test.py

3 结果

---

该文章是对《深度学习入门 基于Python的理论与实现》的总结，作者是[日]斋藤康毅

在上一篇博文中，我们观察了各层的激活值分布，并从中了解到如果设定了合适的权重初始值，则各层的激活值分布会有适当的广度，从而可以顺利地进行学习。那么，为了使各层拥有适当的广度，“强制性”地调整激活值的分布会怎样呢？实际上，Batch Normalization 方法就是基于这个想法而产生的。--------增加适当广度（调整激活值的分布）

1、Batch Normalization算法

Batch Normalization（下文简称Batch Norm）是2015年提出的方法。Batch Norm虽然是一个问世不久的新方法，但已经被很多研究人员和技术人员广泛使用。

优点：
            • 可以使学习快速进行（可以增大学习率）。
            • 不那么依赖初始值（对于初始值不用那么神经质）。
            • 抑制过拟合（降低Dropout等的必要性）。

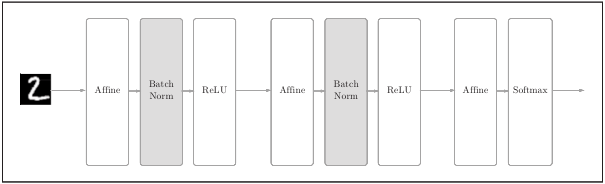
下图为使用了Batch Normalization的神经网络的例子

Batch Norm，顾名思义，以进行学习时的mini-batch为单位，按mini-batch进行正规化。具体而言，就是进行使数据分布的均值为0、方差为1的正规化。用数学式表示的话，如下所示。

【注】这里对mini-batch的m个输入数据的集合B = {x 1 , x 2 , . . . , x m }求均值µ B 和方差 。然后，对输入数据进行均值为0、方差为1（合适的分布）的正规化。ε是一个微小值（比如， 10e-7 等），它是为了防止出现除以0的情况。第二个式子所做的是将mini-batch的输入数据{x 1 , x 2 , . . . , x m }变换为均值为0、方差为1的数据 。通过将这个处理插入到激活函数的前面（或者后面）
，可以减小数据分布的偏向

接着，Batch Norm层会对正规化后的数据进行缩放和平移的变换，用数学式可以如下表示。

【注】γ和β是参数。开始时γ = 1，β = 0，然后再通过学习调整到合适的值。

上面就是Batch Norm的算法。这个算法是神经网络上的正向传播（计算图如下）

 

2、评估

使用MNIST数据集观察使用Batch Norm层和不使用Batch Norm层时学习的过程会如何变化

目录文件如下：

对于（funtions.py, gradient.py, layers.py,  optimizer.py, util.py）见前面博文

2.1、common/multi_layer_net_extend.py

# coding: utf-8
import sys, os
sys.path.append(os.pardir)
import numpy as np
from collections import OrderedDict
from common.layers import *
from common.gradient import numerical_gradient


class MultiLayerNetExtend:
    """
    Weiht Decay、Dropout、Batch Normalization

    Parameters
    ----------
    input_size : 784
    hidden_size_list : （ [100, 100, 100]）
    output_size : 10
    activation : 'relu' or 'sigmoid'
    weight_init_std :  0.01
        'relu'： he初始值
        'sigmoid'：Xavier初始值
    weight_decay_lambda : Weight Decay（
    use_dropout: Dropout
    dropout_ration : Dropout
    use_batchNorm: Batch Normalization
    """
    def __init__(self, input_size, hidden_size_list, output_size,
                 activation='relu', weight_init_std='relu', weight_decay_lambda=0, 
                 use_dropout = False, dropout_ration = 0.5, use_batchnorm=False):
        self.input_size = input_size
        self.output_size = output_size
        self.hidden_size_list = hidden_size_list
        self.hidden_layer_num = len(hidden_size_list)
        self.use_dropout = use_dropout
        self.weight_decay_lambda = weight_decay_lambda
        self.use_batchnorm = use_batchnorm
        self.params = {}

        # 权重初始化
        self.__init_weight(weight_init_std)

        # 激活函数层
        activation_layer = {'sigmoid': Sigmoid, 'relu': Relu}
        self.layers = OrderedDict()
        for idx in range(1, self.hidden_layer_num+1):
            self.layers['Affine' + str(idx)] = Affine(self.params['W' + str(idx)],
                                                      self.params['b' + str(idx)])
            if self.use_batchnorm:
                self.params['gamma' + str(idx)] = np.ones(hidden_size_list[idx-1])
                self.params['beta' + str(idx)] = np.zeros(hidden_size_list[idx-1])
                self.layers['BatchNorm' + str(idx)] = BatchNormalization(self.params['gamma' + str(idx)], self.params['beta' + str(idx)])
                
            self.layers['Activation_function' + str(idx)] = activation_layer[activation]()
            
            if self.use_dropout:
                self.layers['Dropout' + str(idx)] = Dropout(dropout_ration)

        idx = self.hidden_layer_num + 1
        self.layers['Affine' + str(idx)] = Affine(self.params['W' + str(idx)], self.params['b' + str(idx)])

        self.last_layer = SoftmaxWithLoss()

    # 初始化权重
    def __init_weight(self, weight_init_std):
        """
        Parameters
        ----------
        weight_init_std : 标准差为0.01
            'relu'：He初始值
            'sigmoid'：Xavier初始值
        """
        all_size_list = [self.input_size] + self.hidden_size_list + [self.output_size]
        for idx in range(1, len(all_size_list)):
            scale = weight_init_std
            if str(weight_init_std).lower() in ('relu', 'he'):
                scale = np.sqrt(2.0 / all_size_list[idx - 1])  # ReLU初始值
            elif str(weight_init_std).lower() in ('sigmoid', 'xavier'):
                scale = np.sqrt(1.0 / all_size_list[idx - 1])  # sigmoid初始值
            self.params['W' + str(idx)] = scale * np.random.randn(all_size_list[idx-1], all_size_list[idx])
            self.params['b' + str(idx)] = np.zeros(all_size_list[idx])

    def predict(self, x, train_flg=False):
        for key, layer in self.layers.items():
            if "Dropout" in key or "BatchNorm" in key:
                x = layer.forward(x, train_flg)
            else:
                x = layer.forward(x)

        return x

    def loss(self, x, t, train_flg=False):
        """损失函数
        """
        y = self.predict(x, train_flg)

        weight_decay = 0
        for idx in range(1, self.hidden_layer_num + 2):
            W = self.params['W' + str(idx)]
            weight_decay += 0.5 * self.weight_decay_lambda * np.sum(W**2)

        return self.last_layer.forward(y, t) + weight_decay

    def accuracy(self, X, T):
        """
        计算精度
        :param X:
        :param T:
        :return:
        """
        Y = self.predict(X, train_flg=False)
        Y = np.argmax(Y, axis=1)
        if T.ndim != 1:
            T = np.argmax(T, axis=1)

        accuracy = np.sum(Y == T) / float(X.shape[0])
        return accuracy

    def numerical_gradient(self, X, T):
        """计算梯度(数值微分)
        Parameters
        ----------
        X : 训练集
        T : 训练标签

        Returns
        -------
        每层的参数的梯度
            grads['W1']、grads['W2']、...各层权重梯度值
            grads['b1']、grads['b2']、...各层偏置梯度值
        """
        loss_W = lambda W: self.loss(X, T, train_flg=True)

        grads = {}
        for idx in range(1, self.hidden_layer_num+2):
            grads['W' + str(idx)] = numerical_gradient(loss_W, self.params['W' + str(idx)])
            grads['b' + str(idx)] = numerical_gradient(loss_W, self.params['b' + str(idx)])
            
            if self.use_batchnorm and idx != self.hidden_layer_num+1:
                grads['gamma' + str(idx)] = numerical_gradient(loss_W, self.params['gamma' + str(idx)])
                grads['beta' + str(idx)] = numerical_gradient(loss_W, self.params['beta' + str(idx)])

        return grads
        
    def gradient(self, x, t):
        # forward
        self.loss(x, t, train_flg=True)

        # backward
        dout = 1
        dout = self.last_layer.backward(dout)

        layers = list(self.layers.values())
        layers.reverse()
        for layer in layers:
            dout = layer.backward(dout)

        #
        grads = {}
        for idx in range(1, self.hidden_layer_num+2):
            grads['W' + str(idx)] = self.layers['Affine' + str(idx)].dW + self.weight_decay_lambda * self.params['W' + str(idx)]
            grads['b' + str(idx)] = self.layers['Affine' + str(idx)].db

            if self.use_batchnorm and idx != self.hidden_layer_num+1:
                grads['gamma' + str(idx)] = self.layers['BatchNorm' + str(idx)].dgamma
                grads['beta' + str(idx)] = self.layers['BatchNorm' + str(idx)].dbeta

        return grads

2.2、batch_norm_test.py

# coding: utf-8
import sys, os
sys.path.append(os.pardir)
import numpy as np
import matplotlib.pyplot as plt
from dataset.mnist import load_mnist
from common.multi_layer_net_extend import MultiLayerNetExtend
from common.optimizer import SGD, Adam


(x_train, t_train), (x_test, t_test) = load_mnist(normalize=True)

# 减少学习数据
x_train = x_train[:1000]
t_train = t_train[:1000]

max_epochs = 20
train_size = x_train.shape[0]
batch_size = 100
learning_rate = 0.01


def __train(weight_init_std):
    bn_network = MultiLayerNetExtend(input_size=784, hidden_size_list=[100, 100, 100, 100, 100], output_size=10, 
                                    weight_init_std=weight_init_std, use_batchnorm=True)
    network = MultiLayerNetExtend(input_size=784, hidden_size_list=[100, 100, 100, 100, 100], output_size=10,
                                weight_init_std=weight_init_std)
    optimizer = SGD(lr=learning_rate)
    
    train_acc_list = []
    bn_train_acc_list = []
    
    iter_per_epoch = max(train_size / batch_size, 1)  # 10
    epoch_cnt = 0

    # 训练的次数
    for i in range(1000000000):
        batch_mask = np.random.choice(train_size, batch_size)
        x_batch = x_train[batch_mask]
        t_batch = t_train[batch_mask]
    
        for _network in (bn_network, network):
            grads = _network.gradient(x_batch, t_batch)
            optimizer.update(_network.params, grads)
    
        if i % iter_per_epoch == 0:  # 10
            train_acc = network.accuracy(x_train, t_train)
            bn_train_acc = bn_network.accuracy(x_train, t_train)
            train_acc_list.append(train_acc)
            bn_train_acc_list.append(bn_train_acc)
    
            print("epoch: " + str(epoch_cnt) + " | " + str(train_acc) + " - " + str(bn_train_acc))
    
            epoch_cnt += 1
            if epoch_cnt >= max_epochs:  # 20
                break
                
    return train_acc_list, bn_train_acc_list


# 3.绘制图表==========
# logspac用于创建等比数列,开始点和结束点是10的幂，共有16个数
weight_scale_list = np.logspace(0, -4, num=16)
x = np.arange(max_epochs)

# 类似枚举类型
# i: 16, w: value
for i, w in enumerate(weight_scale_list):
    print("============== " + str(i+1) + "/16" + " ==============")
    train_acc_list, bn_train_acc_list = __train(w)
    
    plt.subplot(4, 4, i+1)
    plt.title("W:" + str(w))
    if i == 15:
        plt.plot(x, bn_train_acc_list, label='Batch Normalization', markevery=2)
        plt.plot(x, train_acc_list, linestyle="--", label='Normal(without BatchNorm)', markevery=2)
    else:
        plt.plot(x, bn_train_acc_list, markevery=2)
        plt.plot(x, train_acc_list, linestyle="--", markevery=2)

    plt.ylim(0, 1.0)
    if i % 4:
        plt.yticks([])
    else:
        plt.ylabel("accuracy")
    if i < 12:
        plt.xticks([])
    else:
        plt.xlabel("epochs")
    plt.legend(loc='lower right')
    
plt.show()
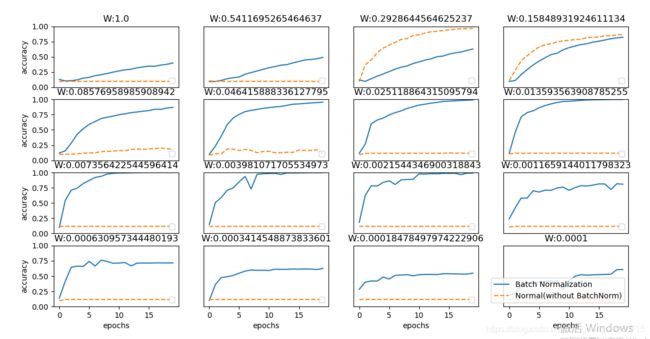
# 共由16个权值，

3 结果

【注】此处使用了16个不同的初始权值，图中都说明了Batch Normalization的学习速度更快