数据结构与算法:插入排序&希尔排序
数据结构与算法:插入排序&希尔排序
-
- 插入排序
- 希尔排序
插入排序
假设现在你有一个有序的数组,你要把一个数据插入到数组中,保证插入后依然有序,要怎么做?
对于人来说,这个问题就像是在整理扑克牌,瞄一眼就知道应该插入什么位置。但是对于程序来说,就需要一一对比,直到找到一个位置左边比它大,右边比它小,就算找到了一合适的位置插入。
而插入排序就是基于这样的一个过程完成的排序。
我们只需要将第一个无序的元素进行插入,向右一一对比,就可以找到合适的位置。
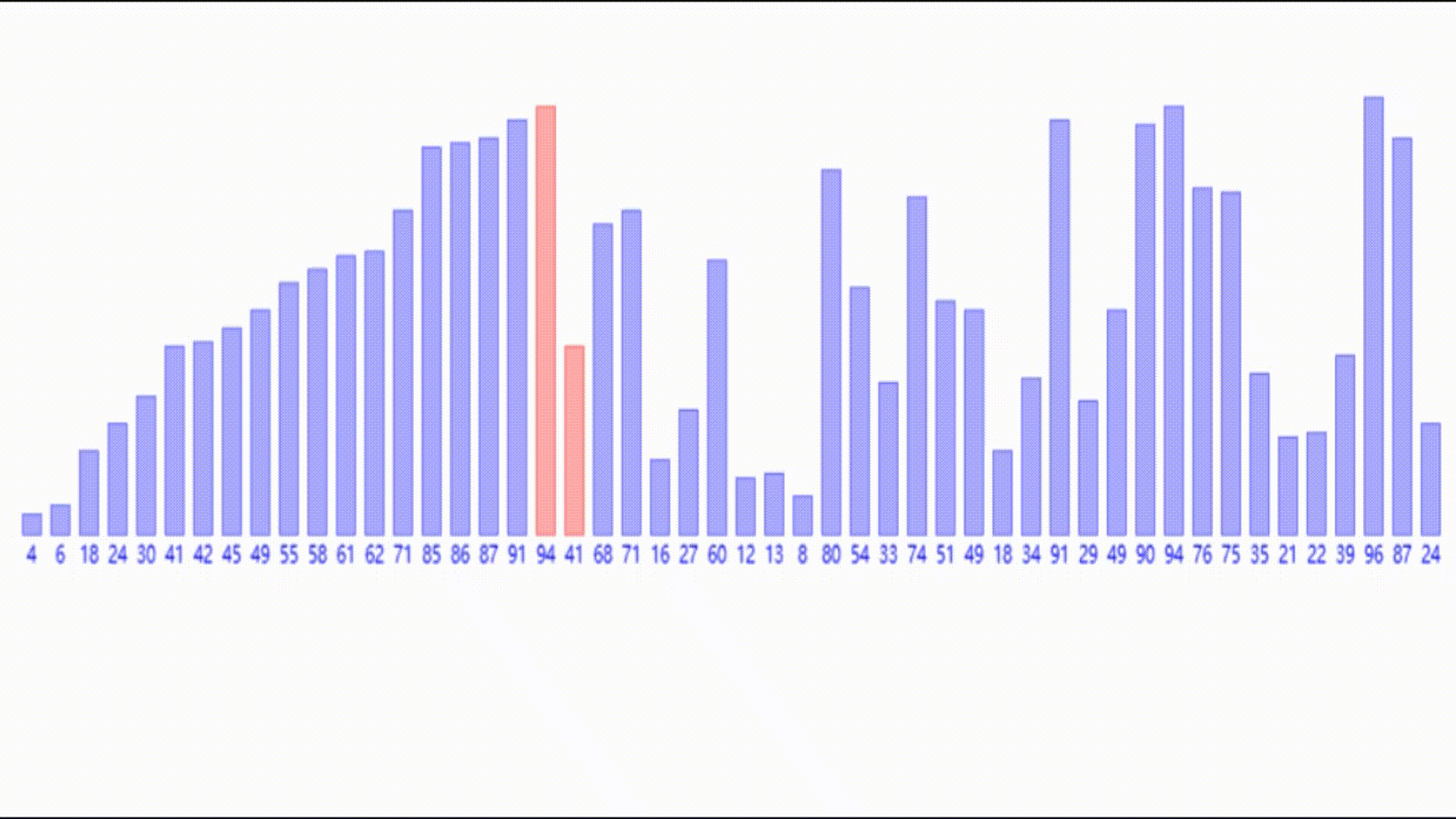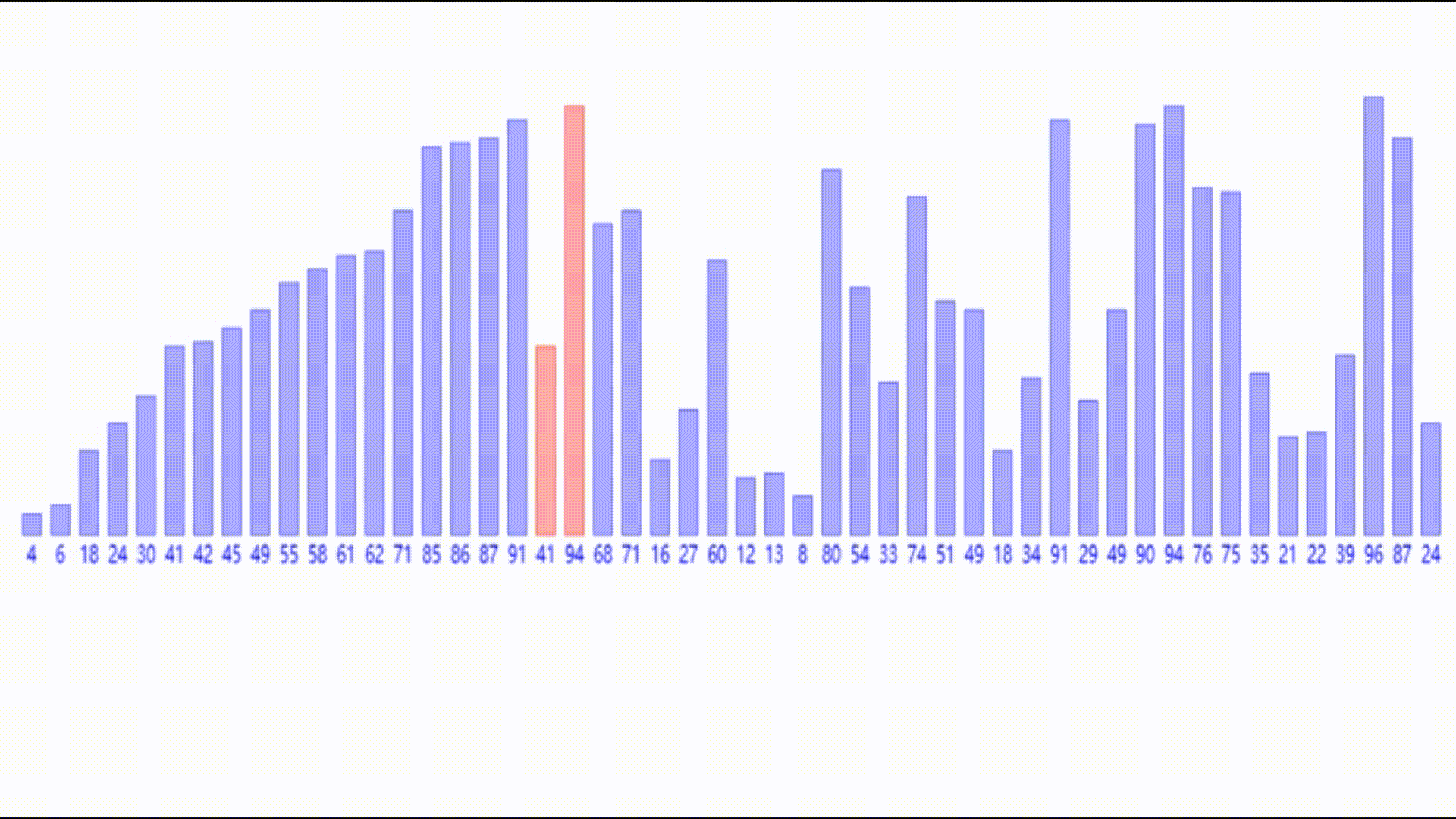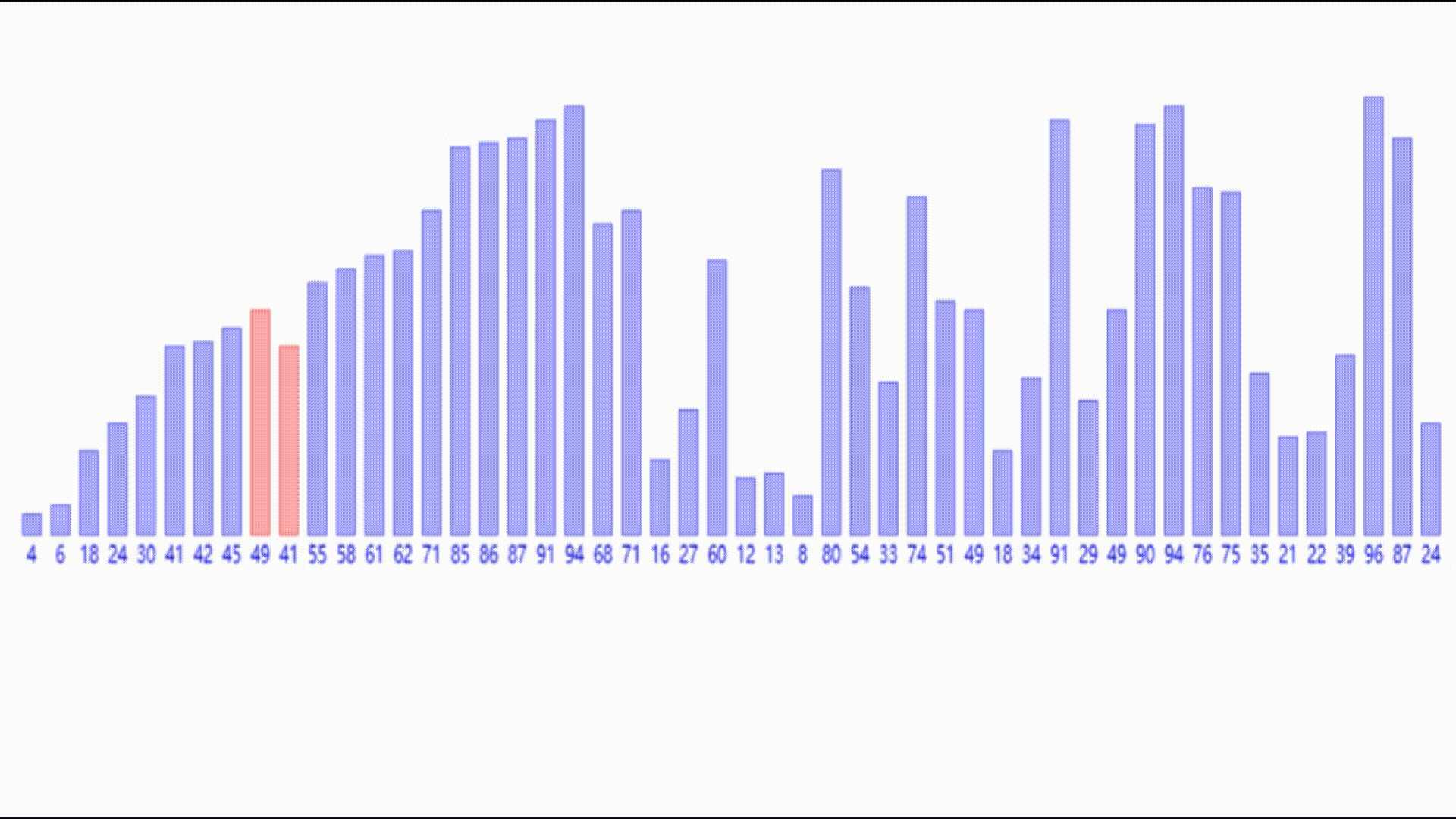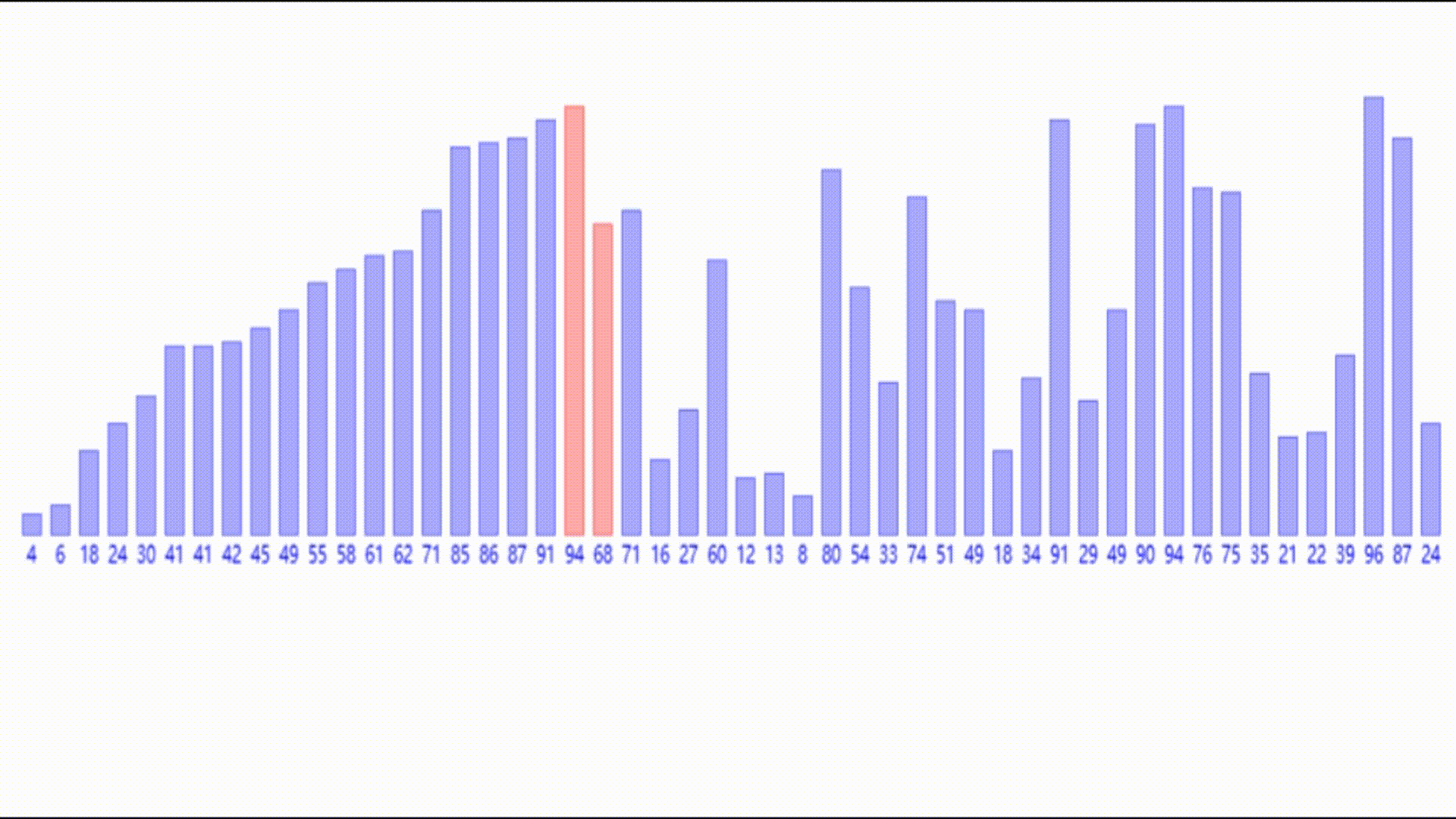
那么如果一个数组完全无序,要如何利用这个插入的思想呢?
比如对于以下数组:
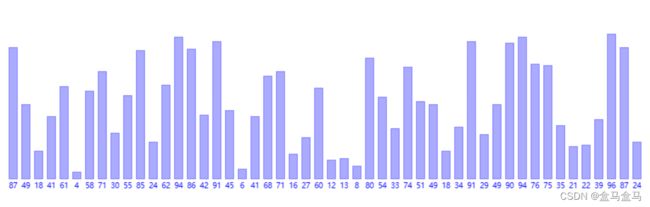
我们可以将其视为:第一个元素有序,插入第二个元素:
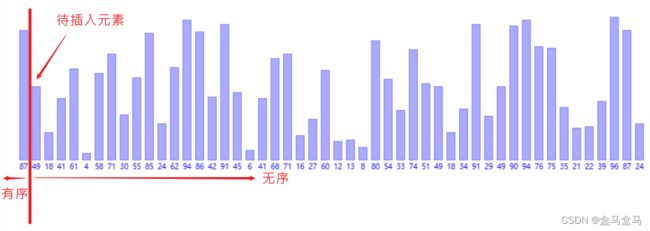
当插入第二个元素,前两个元素就是有序的,然后插入第三个元素;接着前三个元素就是有序的,插入第四个元素…以此类推
最后前n-1个元素是有序的,第n个元素是无序的,插入第n个元素,最后整个数组都是有序的了。
过程如下:
代码实现:
// 插入排序
void InsertSort(int* a, int n)
{
for (int i = 0; i < n - 1; i++)
{
//设前[0, end]是一个有序数列,将end+1插入
int end = i;
int tmp = a[end + 1];
while (end >= 0)
{
if (tmp < a[end])
{
a[end + 1] = a[end];
--end;
}
else
{
break;
}
}
a[end + 1] = tmp;
}
}
具体解释如下:
- 函数定义了一个名为
InsertSort的函数,接收两个参数:一个整型数组a和一个整型变量n,表示数组的元素个数。
- 使用一个循环遍历数组
a,循环变量i从0开始,每次循环递增1,直到i大于或等于n-1。
- 在每次循环中,将数组的第
i个元素设为待插入的元素,即end+1处的元素。
- 定义一个整型变量
end,初始值为i,用于表示有序数列的末尾位置。
- 将
end+1处的元素暂存到变量tmp中。
- 使用一个循环将
end+1处的元素插入到有序数列中。循环条件是end大于等于0,也就是当end等于0时,说明已经遍历到了有序数列的开头。
- 在循环内部,判断
tmp与a[end]的大小关系。如果tmp小于a[end],则将a[end]后移一位,end递减1。这样,比tmp大的元素就会向右移动一位,为tmp腾出插入的位置。
- 如果
tmp大于或等于a[end],则说明tmp应该插入到end+1的位置。同时跳出循环。
- 在跳出循环后,将
tmp插入到end+1的位置,即a[end+1] = tmp。
- 重复步骤2~9,直到遍历完整个数组a,排序完成。
希尔排序
希尔排序(Shell Sort)是插入排序的一种,它是针对直接插入排序算法的改进。
希尔排序又称缩小增量排序,因 DL.Shell 于 1959 年提出而得名。
假设我们现在有一个完全逆序的数组,如果此时使用插入排序对其排序,那么第二个元素就要和第一个元素交换,第三个元素要和前两个全部交换一一次…第n个元素要和前n-1个元素交换一次,这不是把时间复杂度拉满了吗。
于是有人就开始考虑要如何处理这种逆序环境下插入排序要全部交换一次的问题。
插入排序在这种情况下排序效率低的原因在于,当一个比较小的元素处于后面时,其要和前面的所有比他大的元素对比一次,比如这样:
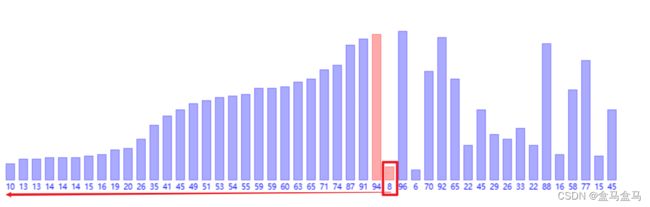
这个8想要到达正确位置,就要和前面所有的元素进行一次比大小,这会造成很多的计算量,想要优化这个问题,其实就是解决:如何让比较小的元素快速到达数组的前面?
于是希尔排序诞生了,我们可以将一个数组分为分为多组,对每一组单独进行一次插入排序,比如这样:
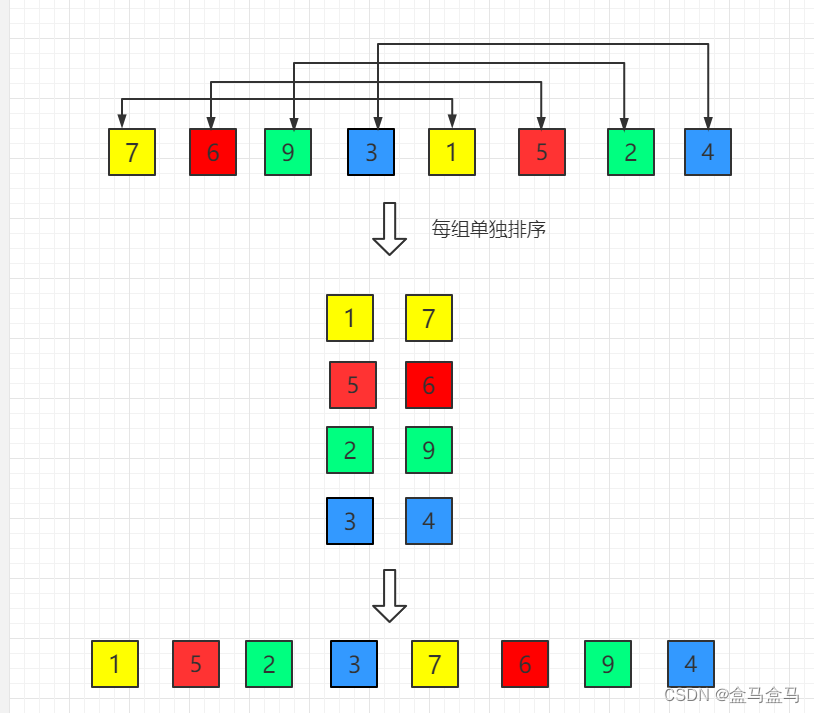
这是一个8个数字的数组,我们将其分为4份,每两个数字一组,上面每种颜色为一组,然后让他们进行一次插入排序。排序后,虽然数组依然无序,但是整体上来说,前面的数字比较小,后面的数字比较大,通过这种方法,可以将后面的小元素快速提到前面。
我们再利用一个较大的数据看一次:
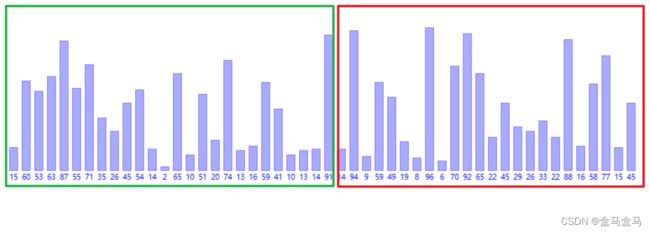
我们现在对这个数组分区,分为两份,左边是一份,右边是一份。其中左边的第一个元素和右边的第一个元素是一组,左边的第二个元素和右边的第二个元素是一组…左边的最后一个元素和右边的最后一个元素是一组。
这样我们就把这个数组分为了两两一组,然后每两个元素进行一次插入排序:
这样一趟排序后,我们看看数组的状态:
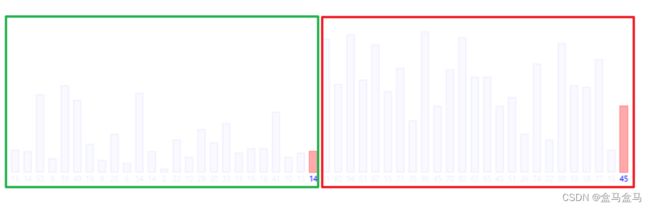
整体上来说,左边的数据要小于右边的数据,这不就达成了我们想要的效果:让比较小的元素快速到达数组的前面。这个过程,每个数据都只进行了一次交换,就到达了比较前的位置。这个过程叫做预排序
希尔排序是基于插入排序的算法,通过分组对元素进行插入排序来提高效率。
上述过程的代码如下:
int gap = n / 2;
for (int i = 0; i < n - gap; i++)
{
int end = i;
int tmp = a[end + gap];
while (end >= 0)
{
if (tmp < a[end])
{
a[end + gap] = a[end];
end -= gap;
}
else
{
break;
}
}
a[end + gap] = tmp;
}
首先,定义一个变量 gap,其值为数组的长度 n 除以 2。gap 的值决定了分组的大小,可以根据具体情况进行调整。
然后,使用一个循环遍历数组 a,从前往后依次处理每个元素。循环的结束条件是 i < n - gap,即遍历到倒数第 gap 个元素时结束。
在循环内部,首先定义一个变量 end,并将其赋值为当前遍历的元素下标 i。然后,定义一个变量 tmp,并将其赋值为 a[end + gap],即当前元素所在分组的下一个元素。
接下来,使用一个循环将当前元素插入到正确的位置。循环的条件是 end >= 0,即遍历到数组的起始位置时结束。在循环内部,做如下操作:
- 如果
tmp的值小于当前位置的元素a[end],则将a[end]的值赋给a[end + gap],并将end的值减去gap。 - 如果
tmp的值大于等于当前位置的元素a[end],则退出循环。
最后,将 tmp 的值赋给最终位置上的元素,即 a[end + gap]。
但是这样还不是一个完整的希尔排序,设想一下,如果我们的数据量很庞大,是不是要多进行几次预排序才比较好?这样小的数据才更可能再数组的前面。
所以我们的gap也是动态变化的,在希尔排序中,一开始我们两两一组进行了插入排序,我们可以再进行4个一组插入排序,接着8个一组插入排序…以此类推,直到n个一组,将整个数组作为一组是,也就是最后一趟插入排序,这时候数组已经十分接近有序,最后对整个数组进行一次插入排序,数组就有序了。
过程如下:
经过这一次每四个一组的排序,我们的数组状态如下:
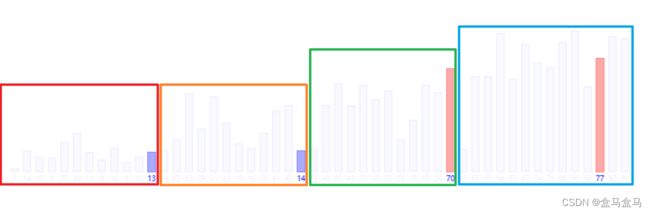
可以看到,数组整体呈阶梯递增趋势了。
接着进行后续排序:
可以发现,数组越来越接近有序,最后一趟排序,几乎每个元素都没有移动几次就插入到了目标位置,这就是希尔排序的完整推导思路。
外层控制gap的代码如下:
// 希尔排序
void ShellSort(int* a, int n)
{
int gap = n;
while (gap > 1)
{
gap = gap / 2;
//插入排序
}
}
在这段代码中,首先定义了一个变量gap,它表示初始的增量,也即是划分的分组的大小。初始化时,gap的值为待排序数组的大小n。
然后,代码进入一个while循环,循环条件是gap > 1,也就是说当gap为1时,循环结束。在每一轮循环中,gap的值减半,并更新为新的增量。这样,希尔排序就是通过不断缩小增量的大小来进行排序。
在每一轮循环中,代码执行了一个"插入排序"的操作。
最终,当增量gap减小到1时,希尔排序的整个过程结束,待排序数组完成排序。
总代码如下:
// 希尔排序
void ShellSort(int* a, int n)
{
int gap = n;
while (gap > 1)
{
gap = gap / 2;
for (int i = 0; i < n - gap; i++)
{
int end = i;
int tmp = a[end + gap];
while (end >= 0)
{
if (tmp < a[end])
{
a[end + gap] = a[end];
end -= gap;
}
else
{
break;
}
}
a[end + gap] = tmp;
}
}
}
