用于图节点分类的标签传播系列算法

Label Propagation for Node Classification

本节是CSW224第一部分的最后一节

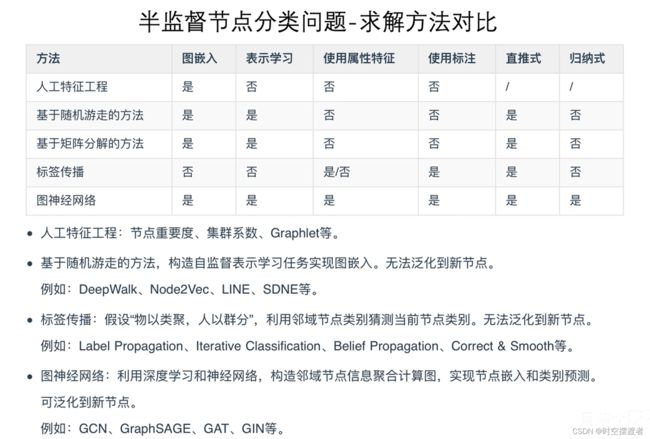
标签传播（Label Propagation）或（消息传递Message passing）经常被用作一个Baseline。这也是一种半监督节点分类（semi-supervised node classification），用一部分已知标签的节点去预测剩下的未知标签的节点。

注意：半监督与监督学习不同，这里没有将已经学到的模型泛化到新来的节点上，仅仅是对原图的剩余节点进行分类，因为在学习模型时，原图的未知标签的节点也可能用于训练。这种被称为直推式学习（Transductive），与之相对应的是归纳式学习（Inductive）。

对于图神经网络，是可以做到归纳式学习。

基本假设：

网络中的节点是 物以类聚，人以群分（Correlation / dependencies）。关与这个基本假设可以从以下两个方面解释。

1. Homophily同质性：具有相似属性的节点更可能属于同一类或同一群体。“Birds of a feather flock together” 有相同羽毛的鸟可能在一起飞翔

2. Influence 连接：，物以类聚，人以群分；近朱者赤，近墨者黑。
   

思路

例如KNN最近邻分类，根据节点连接到的其他节点的标签，对我进行分类。例如不良网站之间总是互相引流。

• 节点自身特征
• 节点的邻域节点的特征和属性

collective classification

Label Propagation（Relational classification）

对于带权图，通过迭代方式进行加权平均；对无权图，则进行平均。其中$Y_v$表示节点$v$是类别$c$的概率

$$P\left(Y_v=c\right)=\frac{1}{{\sum }_{(v,u)\in E}{A}_{v,u}}\sum _{(v,u)\in E}{A}_{v,u}P\left(Y_u=c\right)$$

这种方法有两个缺点：

1. 不能保证一定收敛
2. 只用到了连接信息，没有用到节点的特征。

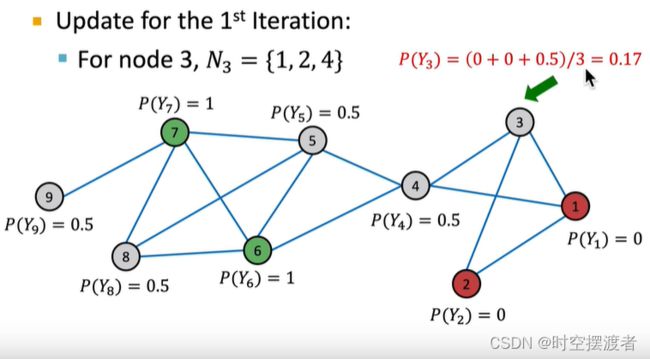
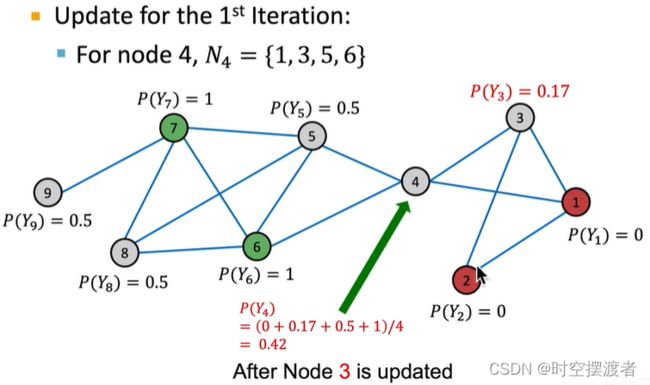
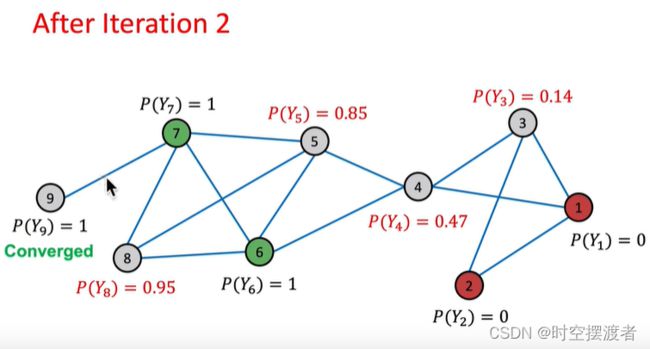
算法运行时，可以为各节点标号，按顺序进行迭代计算灰色节点的类别概率。灰色节点所属类别的概率初始化为0.5

在一轮完成后，发现某些节点的类别概率达到1或者0，或者是某个阈值时，即为收敛。后续按照这个流程进行多轮迭代，直到达到最大次数或者所有灰色节点均已收敛。

注意：nx.label_propagation_communities算法只适用于无向图

import networkx as nx
from networkx.algorithms import community
G = nx.karate_club_graph()
communities = community.label_propagation_communities(G)
# 获得每个社群的节点
community_list = []
for community in communities:
    community_list.append(list(community))
# 为每个社群的节点分类
node_colors = []
for n in G:
    if n in community_list[0]:
        node_colors.append('blue')
    elif n in community_list[1]:
        node_colors.append('red')
    else:
        node_colors.append('yellow')
# 可视化
nx.draw(G,node_color=node_colors,with_labels=True)

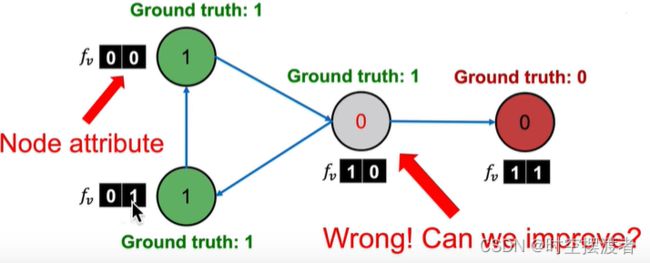
Iterative classification（ICA ）

由于之前的算法没有考虑节点的特征，因此本算法构建两个分类器：

1. base classifier $\varphi (f_v)$：使用节点属性特征
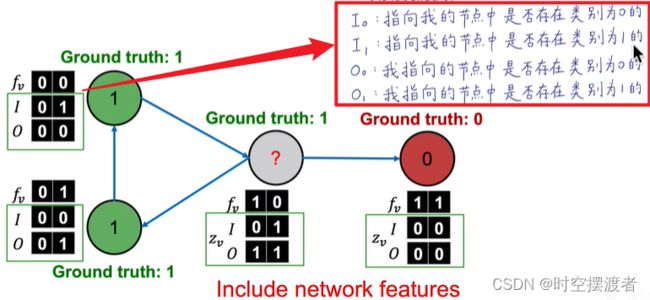
2. relational classifier $\varphi (f_v,Z_v)$：使用节点属性特征和网络连接特征（$z_v$是自定义的节点$v$的相邻节点的特征向量）

对于$Z_v$的计算，主要思想是提取节点周围节点类别信息，形成一个向量，有以下思路供参考

1. 邻居节点各类别的节点数
2. 邻居节点中最常见的类别
3. 有多少种不同类别
4. …开开脑洞吧

流程

Phase1

在已标注的训练集上，训练两个分类器。

1. ${\varphi }_1(f_v)$
2. ${\varphi }_2(f_v,Z_v)$

Phase2：迭代直到收敛

1. 在未标注的节点上，用${\varphi }_1(f_v)$预测 $Y_v$
2. 使用$Y_v$计算 （之后迭代更新）$Z_v$
3. 使用${\varphi }_2(f_v,Z_v)$ 计算所有节点类别
4. 至此，图中所有节点类别均已标注
5. 返回第二步，直到收敛或者达到最大迭代次数

缺点：不保证收敛

Example

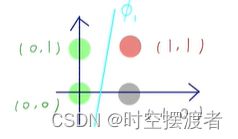
对于上图数据，如果训练一个线性分类器，有可能会错误地将灰色节点分类为红色。

所以不仅要考虑节点的属性特征$f_v$，还要考虑连接特征 $Z_v$。

Correct & Smooth

后处理的思想，类似目标检测中的Softnms

流程

1. 在已标注的数据集上训练一个基础分类器，任意模型
2. 使用基础分类器预测所有节点的soft label，即预测结果是一个概率值，各类别均不为0

3. 后处理（Post-process）

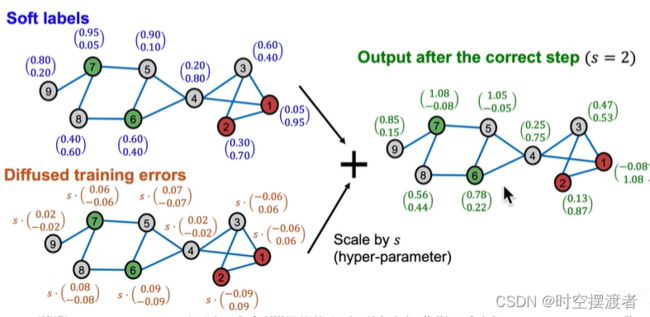
   1. Correct ：对不确定程度进行扩散。认为不确定度在图中也是homophily的。要对不确定性进行分散

      1. 在所有已标注节点计算error = 真实概率 - soft label

      

      2. 得到最初的Error矩阵$E^{(0)}$，并对其削峰填谷，类似Label Propagation。

      

      3. $E^{(t+1)}=(1-\alpha ).E^{(t)}+\alpha .\mathbf{A}{E}^{(t)}$，其中$\mathbf{A}=D^{-\frac{1}{2}}A{D}^{-\frac{1}{2}}$，$\alpha$为超参数，越大，更倾向于传播的Error；越小，更倾向于上一时刻的Error。$\mathbf{A}$表示传播作用。

      

      

      

      4. 最终Correct的结果，需要将最初Soft labels + s.最后的Error。s为超参数

      

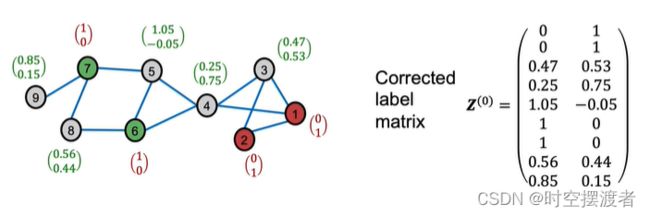
   2. Smooth：原理依旧是基于近朱者赤近墨者黑假设，将结果扩展。将已标注节点的概率和未标注节点经过Correct后的概率组成Z矩阵（Corrected Label matrix）

      

      1. ${\mathbf{Z}}^{(t+1)}\leftarrow (1-\alpha )\cdot {\mathbf{Z}}^{(t)}+\alpha \cdot \mathbf{A}{\mathbf{Z}}^{(t)}$
      2. 在最终的结果，节点所属类别的值并不是概率值，但却能反映概率

Loopy Belief Propagation

思想：节点u认为节点v是类别1的概率是多少，传递消息，当所有节点达到共识时，得到最终结果。

Masked Label Prediction

自监督，收到BERT在NLP领域的启发