机器学习---kMeans算法

1. Load dataset

from numpy import *
import matplotlib.pyplot as plt
import pandas as pd

url = "https://archive.ics.uci.edu/ml/machine-learning-databases/iris/iris.data"
names = ['sepal-length', 'sepal-width', 'petal-length', 'petal-width', 'class'] # 5列
dataset = pd.read_csv(url, names=names)
dataset['class'][dataset['class']=='Iris-setosa']=0
dataset['class'][dataset['class']=='Iris-versicolor']=1
dataset['class'][dataset['class']=='Iris-virginica']=2

鸢（yuan1）尾花卉数据集，是一类多重变量分析的数据集。数据集包含150个数据集，分为3类，

每类50个数据，每个数据包含4个属性。可通过花萼长度，花萼宽度，花瓣长度，花瓣宽度4个属

性预测鸢尾花卉属于（Setosa，Versicolour，Virginica）三个种类中的哪一类。#对类别进行编

码，3个类别分别赋值0，1，2。

2. 计算距离

def distEclud(vecA, vecB):                  
    return sqrt(sum(power(vecA - vecB, 2)))

计算两个向量之间的欧氏距离。输入: 两个向量vecA和vecB。

使用公式：

3. 初始化聚类中心

# def randCent(dataSet, k):
#     #获取特征维度
#     n = shape(dataSet)[1]   
#     #创建聚类中心0矩阵 k x n
#     centroids = mat(zeros((k,n)))
#     #遍历n维特征         
#     for j in range(n):     
#         #第j维特征属性值min   ,1x1矩阵                 
#         minJ = min(dataSet[:,j])        
#         #区间值max-min，float数值    
#         rangeJ = float(max(dataSet[:,j]) - minJ)   
#         #第j维，每次随机生成k个中心
#         centroids[:,j] = mat(minJ + rangeJ * random.rand(k,1))
#     return centroids

def randChosenCent(dataSet,k):
    # 样本数
    m=shape(dataSet)[0]
    # 初始化列表
    centroidsIndex=[]
    #生成类似于样本索引的列表
    dataIndex=list(range(m))
    for i in range(k):
        #生成随机数
        randIndex=random.randint(0,len(dataIndex))
        #将随机产生的样本的索引放入centroidsIndex
        centroidsIndex.append(dataIndex[randIndex])
        #删除已经被抽中的样本
        del dataIndex[randIndex]
    #根据索引获取样本
    centroids = dataSet.iloc[centroidsIndex]
    return mat(centroids)

随机选择k个样本作为初始聚类中心。获取数据集的样本数（m），创建一个空列表centroidsIndex

来存储选中的样本索引，创建一个与数据集样本数相同长度的索引列表dataIndex，循环k次，每次

随机选择dataIndex中的一个索引加入centroidsIndex，然后从dataIndex中移除它，使用这些索引

从数据集中提取对应的样本。

4. KMeans

创建一个矩阵clusterAssment用于存储每个点的簇分配和距离平方，使用randChosenCent初始化k

个聚类中心。对于数据集中的每个样本，找到最近的聚类中心，并更新clusterAssment。更新聚类

中心为分配给该簇的所有点的均值。如果有样本的簇分配发生变化，重复迭代步骤。当没有更多的

簇分配变化时停止迭代。

def kMeans(dataSet, k):
    # 样本总数
    m = shape(dataSet)[0] # 150*2
    #分配样本到最近的簇：存[簇序号,距离的平方]
    # m行  2 列
    clusterAssment = mat(zeros((m,2)))

    #step1:
    #通过随机产生的样本点初始化聚类中心
    centroids = randChosenCent(dataSet, k)
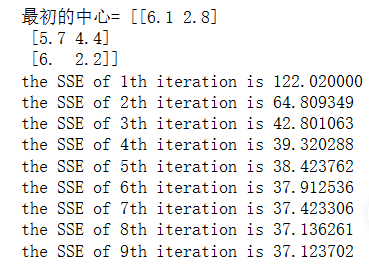
    print('最初的中心=',centroids)

    #标志位，如果迭代前后样本分类发生变化值为True，否则为False
    clusterChanged = True
    #查看迭代次数
    iterTime=0
    #所有样本分配结果不再改变，迭代终止
    while clusterChanged:   
        clusterChanged = False        
        #step2:分配到最近的聚类中心对应的簇中
        for i in range(m):
            #初始定义距离为无穷大
            minDist = inf;
            #初始化索引值
            minIndex = -1
            # 计算每个样本与k个中心点距离
            for j in range(k):
                #计算第i个样本到第j个中心点的距离
                distJI = distEclud(centroids[j,:],dataSet.values[i,:])
                #判断距离是否为最小
                if distJI < minDist:
                    #更新获取到最小距离
                    minDist = distJI
                    #获取对应的簇序号
                    minIndex = j
            #样本上次分配结果跟本次不一样，标志位clusterChanged置True
            if clusterAssment[i,0] != minIndex:
                clusterChanged = True
            clusterAssment[i,:] = minIndex,minDist**2 #分配样本到最近的簇
        iterTime+=1
        sse=sum(clusterAssment[:,1])
        print('the SSE of %d'%iterTime + 'th iteration is %f'%sse)
        #step3:更新聚类中心
        for cent in range(k):#样本分配结束后，重新计算聚类中心
            #获取该簇所有的样本点
            # nonzero函数是numpy中用于得到数组array中非零元素的位置（数组索引）的函数。
            # 它的返回值是一个长度为a.ndim(数组a的轴数)的元组，元组的每个元素都是一个整数数组，其值为非零元素的下标在对应轴上的值。
            ptsInClust = dataSet.iloc[nonzero(clusterAssment[:,0].A==cent)[0]] # python中一个matrix矩阵名.A代表将 矩阵转化为array数组类型.
            #更新聚类中心：axis=0沿列方向求均值。
            centroids[cent,:] = mean(ptsInClust, axis=0) 
    return centroids, clusterAssment
# def kMeansSSE(dataSet,k,distMeas=distEclud, createCent=randChosenCent):
#     m = shape(dataSet)[0]
#     #分配样本到最近的簇：存[簇序号,距离的平方]
#     clusterAssment=mat(zeros((m,2)))
#     #step1:#初始化聚类中心
#     centroids = createCent(dataSet, k)
#     print('initial centroids=',centroids)
#     sseOld=0
#     sseNew=inf
#     iterTime=0 #查看迭代次数
#     while(abs(sseNew-sseOld)>0.0001):
#         sseOld=sseNew
#         #step2:将样本分配到最近的质心对应的簇中
#         for i in range(m):
#             minDist=inf;minIndex=-1
#             for j in range(k):
#                 #计算第i个样本与第j个质心之间的距离
#                 distJI=distMeas(centroids[j,:],dataSet.values[i,:])
#                 #获取到第i样本最近的质心的距离,及对应簇序号
#                 if distJI

在kMeans函数中，计算最近的聚类中心和更新聚类中心的步骤是关键。对于每个样本点，函数计

算它到每个中心的距离，选择最近的中心作为其簇，并相应更新clusterAssment。然后，对于每个

簇，函数计算所有分配到该簇的点的均值，以此更新聚类中心的位置。这个过程重复进行，直到达

到稳定状态，即没有更多的簇分配变化。

5. 2维数据聚类效果显示

#2维数据聚类效果显示
def datashow(dataSet,k,centroids,clusterAssment):  #二维空间显示聚类结果
    from matplotlib import pyplot as plt
    num,dim=shape(dataSet)  #样本数num ,维数dim
    
    if dim!=2:
        print('sorry,the dimension of your dataset is not 2!')
        return 1
    marksamples=['or','ob','og','ok','^r','^b','len(marksamples):
        print('sorry,your k is too large,please add length of the marksample!')
        return 1
    #绘所有样本
    for i in range(num):
        markindex=int(clusterAssment[i,0])#矩阵形式转为int值, 簇序号
        #特征维对应坐标轴x,y；样本图形标记及大小
        # 区分iat,at,iloc,loc;
        # iat,iloc按照索引的位置来进行选取
        # at,loc是按照索引（index）的值来选取
        plt.plot(dataSet.iat[i,0],dataSet.iat[i,1],marksamples[markindex],markersize=6) 

    #绘中心点            
    markcentroids=['o','*','^']#聚类中心图形标记
    label=['0','1','2']
    c=['yellow','pink','red']
    for i in range(k):
        plt.plot(centroids[i,0],centroids[i,1],markcentroids[i],markersize=15,label=label[i],c=c[i])
        plt.legend(loc = 'upper left')
    plt.xlabel('sepal length')  
    plt.ylabel('sepal width') 
   
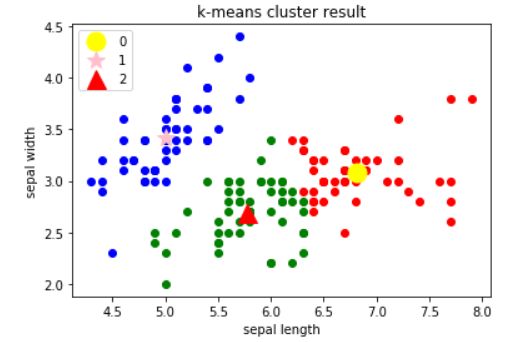
    plt.title('k-means cluster result') #标题        
    plt.show()

在二维空间中可视化k-均值聚类算法的结果。专门用于展示数据点如何根据k-均值算法被分配到不

同的簇中，并且展示这些簇的中心点。代码通过在二维图表上绘制数据点来展示每个点被分配到的

簇。这是通过为不同的簇使用不同的颜色和/或标记来实现的。聚类中心点被特别标记和着色，以

便于从普通数据点中区分出来。这有助于理解每个簇的大致位置和扩展。如果数据集不是二维的，

如果指定的聚类数超过了预定义的标记样式数量，函数会打印错误消息并退出。

6. 画出实际图像

def trgartshow(dataSet,k,labels):
    from matplotlib import pyplot as plt

    num,dim=shape(dataSet)
    label=['0','1','2']
    marksamples=['ob','or','og','ok','^r','^b','

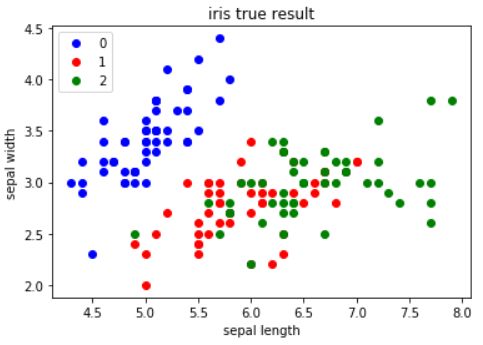
这段代码的主要作用是在二维空间中可视化具有真实类别标签的数据集的散点图。用于展示数据点

按照其实际类别如何分布。这种可视化对于理解数据集的真实分类情况以及评估聚类或其他分类算

法的性能非常有用。dataSet: 要可视化的数据集。k: 类别的数量。labels: 数据集中每个点的真实

类别标签。首先获取数据集的样本数(num)和维度(dim)。使用两个嵌套的循环来绘制数据点。第一

个循环遍历每个数据点，根据其真实类别标签选择颜色和标记样式(marksamples)，然后在图表上

绘制点。第二个循环是为了在图例中只显示每个类别的一个代表，避免图例项重复。它每隔50个点

绘制一个带标签的点。

7. 绘图显示

#聚类前，绘制原始的样本点
def originalDatashow(dataSet):
    #样本的个数和特征维数
    num,dim=shape(dataSet)
    marksamples=['ob'] #样本图形标记
    for i in range(num):
        plt.plot(datamat.iat[i,0],datamat.iat[i,1],marksamples[0],markersize=5)
    plt.title('original dataset')
    plt.xlabel('sepal length')  
    plt.ylabel('sepal width') #标题
    plt.show()

if __name__=='__main__':
    #=====kmeans聚类
    # # #获取样本数据
    datamat=dataset.loc[:, ['sepal-length','sepal-width']]
    #真实的标签
    labels=dataset.loc[:, ['class']]
    # #原始数据显示
    originalDatashow(datamat)

    # #*****kmeans聚类
    k=3 #用户定义聚类数
    mycentroids,clusterAssment=kMeans(datamat, k)
    #mycentroids,clusterAssment=kMeansSSE(datamat,k)

    #绘图显示
    datashow(datamat,k,mycentroids,clusterAssment)
    trgartshow(datamat,3,labels)

整个脚本的主要作用是展示如何在一个实际数据集上实施k-均值聚类，并通过可视化手段展示聚类

前后数据的变化。这包括展示原始数据的分布、聚类算法的输出（即聚类中心和数据点的簇分

配），以及数据的真实类别分布。这样的可视化有助于理解聚类算法在特定数据集上的表现，并与

实际类别进行比较。