如何生成文本: 通过 Transformers 用不同的解码方法生成文本

如何生成文本: 通过 Transformers 用不同的解码方法生成文本

假设 $p=0.92$，Top-p 采样对单词概率进行降序排列并累加，然后选择概率和首次超过 $p=92%$ 的单词集作为采样池，定义为 $V_{\text{top-p}}$。在 $t=1$ 时 $V_{\text{top-p}}$ 有 9 个词，而在 $t=2$ 时它只需要选择前 3 个词就超过了 92%。其实很简单吧！可以看出，在单词比较不可预测时，它保留了更多的候选词，如 $P(w | \text{“The”})$，而当单词似乎更容易预测时，只保留了几个候选词，如 $P(w | \text{“The”}, \text{“car”})$。近年来，随着以 OpenAI GPT2 模型 为代表的基于数百万网页数据训练的大型 Transformer 语言模型的兴起，开放域语言生成领域吸引了越来越多的关注。开放域中的条件语言生成效果令人印象深刻，典型的例子有: GPT2 在独角兽话题上的精彩续写，XLNet 以及 使用 CTRL 模型生成受控文本 等。促成这些进展的除了 transformer 架构的改进和大规模无监督训练数据外，更好的解码方法 也发挥了不可或缺的作用。

本文简述了不同的解码策略，同时向读者展示了如何使用流行的 transformers​ 库轻松实现这些解码策略！

下文中的所有功能均可用于 自回归 语言生成任务 (点击 此处 回顾)。简单复习一下， 自回归 语言生成是基于如下假设: 一个文本序列的概率分布可以分解为每个词基于其上文的条件概率的乘积。

$P(w_{1:T} | W_0 ) = \prod_{t=1}^T P(w_{t} | w_{1: t-1}, W_0) \text{ , 其中 } w_{1: 0} = \emptyset,$

本文绍目前最常用的解码方法，主要有 贪心搜索 (Greedy search) 、波束搜索 (Beam search) 、Top-K 采样 (Top-K sampling) 以及 Top-p 采样 (Top-p sampling) 。

贪心搜索

贪心搜索在每个时间步 $t$ 都简单地选择概率最高的词作为当前输出词: $w_t = argmax_{w}P(w | w_{1:t-1})$ ，如下图所示。

从单词 $\text{“The”}$ 开始，算法在第一步贪心地选择条件概率最高的词 $\text{“nice”}$ 作为输出，依此往后。最终生成的单词序列为 $(\text{“The”}, \text{“nice”}, \text{“woman”})$，其联合概率为 $0.5 \times 0.4 = 0.2$。贪心搜索的主要缺点是它错过了隐藏在低概率词后面的高概率词，如上图所示:

条件概率为 $0.9$ 的单词 $\text{“has”}$ 隐藏在单词 $\text{“dog”}$ 后面，而 $\text{“dog”}$ 因为在 `t=1`​ 时条件概率值只排第二所以未被选择，因此贪心搜索会错过序列 $\text{“The”}, \text {“dog”}, \text{“has”}$ 。

波束搜索

波束搜索通过在每个时间步保留最可能的 num_beams​ 个词，并从中最终选择出概率最高的序列来降低丢失潜在的高概率序列的风险。以 num_beams=2​ 为例:

在时间步 1，除了最有可能的假设 $(\text{“The”}, \text{“nice”})$，波束搜索还跟踪第二可能的假设 $(\text{“The”}, \text{“dog”})$。在时间步 2，波束搜索发现序列 $(\text{“The”}, \text{“dog”}, \text{“has”})$ 概率为$0.36$，比 $(\text{“The”}, \text{“nice”}, \text{“woman”})$ 的 $0.2$ 更高。太棒了，在我们的例子中它已经找到了最有可能的序列！波束搜索一般都会找到比贪心搜索概率更高的输出序列，但仍不保证找到全局最优解。

让我们看看如何在 transformers​ 中使用波束搜索。我们设置 num_beams > 1​ 和 early_stopping=True​ 以便在所有波束达到 EOS 时直接结束生成。

# activate beam search and early_stopping
beam_output = model.generate(
    input_ids, 
    max_length=50, 
    num_beams=5, 
    early_stopping=True
)

print("Output:\n" + 100 * '-')
print(tokenizer.decode(beam_output[0], skip_special_tokens=True))

Output:
----------------------------------------------------------------------------------------------------
I enjoy walking with my cute dog, but I'm not sure if I'll ever be able to walk with him again.

I'm not sure if I'll ever be able to walk with him again. I'm not sure if I'll

虽然结果比贪心搜索更流畅，但输出中仍然包含重复。一个简单的补救措施是引入 n-grams (即连续 n 个词的词序列) 惩罚，该方法是由 Paulus 等人 (2017) 和 Klein 等人 (2017) 引入的。最常见的 n-grams 惩罚是确保每个 n-gram 都只出现一次，方法是如果看到当前候选词与其上文所组成的 n-gram 已经出现过了，就将该候选词的概率设置为 0。但是，n-gram 惩罚使用时必须谨慎，如一篇关于纽约这个城市的文章就不应使用 2-gram 惩罚，否则，城市名称在整个文本中将只出现一次！

波束搜索的另一个重要特性是我们能够比较概率最高的几个波束，并选择最符合我们要求的波束作为最终生成文本。

开放域文本生成的研究人员最近提出了几个理由来说明对该领域而言波束搜索可能不是最佳方案:

• 在机器翻译或摘要等任务中，因为所需生成的长度或多或少都是可预测的，所以波束搜索效果比较好 - 参见 Murray 等人 (2018) 和 Yang 等人 (2018) 的工作。但开放域文本生成情况有所不同，其输出文本长度可能会有很大差异，如对话和故事生成的输出文本长度就有很大不同。
• 我们已经看到波束搜索已被证明存在重复生成的问题。在故事生成这样的场景中，很难用 n-gram 或其他惩罚来控制，因为在“不重复”和最大可重复 n-grams 之间找到一个好的折衷需要大量的微调。
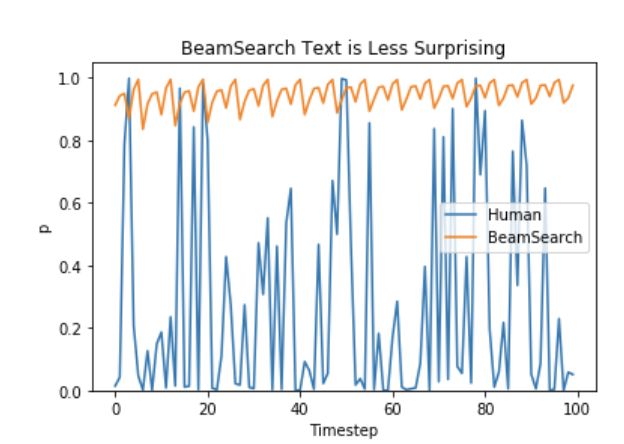
• 正如 Ari Holtzman 等人 (2019) 所论证的那样，高质量的人类语言并不遵循最大概率法则。换句话说，作为人类，我们希望生成的文本能让我们感到惊喜，而可预测的文本使人感觉无聊。论文作者画了一个概率图，很好地展示了这一点，从图中可以看出人类文本带来的惊喜度比波束搜索好不少。

因此，让我们开始玩点刺激的，引入一些随机性。

采样

在其最基本的形式中，采样意味着根据当前条件概率分布随机选择输出词 $w_t$: $w_t \sim P(w|w_{1:t-1})$

继续使用上文中的例子，下图可视化了使用采样生成文本的过程。

很明显，使用采样方法时文本生成本身不再是 确定性的。单词 $\text{“car”}$ 从条件概率分布 $P(w | \text{“The”})$ 中采样而得，而 $\text{“drives”}$ 则采样自 $P(w | \text{“The”}, \text{“car”})$。在 transformers​ 中，我们设置 do_sample=True​ 并通过设置 top_k=0​ 停用 Top-K 采样 (稍后详细介绍)。在下文中，为便于复现，我们会固定 random_seed=0​，但你可以在自己的模型中随意更改 random_seed​。

# set seed to reproduce results. Feel free to change the seed though to get different results
tf.random.set_seed(0)

# activate sampling and deactivate top_k by setting top_k sampling to 0
sample_output = model.generate(
    input_ids, 
    do_sample=True, 
    max_length=50, 
    top_k=0
)

print("Output:\n" + 100 * '-')
print(tokenizer.decode(sample_output[0], skip_special_tokens=True))

Output:
----------------------------------------------------------------------------------------------------
I enjoy walking with my cute dog. He just gave me a whole new hand sense."

But it seems that the dogs have learned a lot from teasing at the local batte harness once they take on the outside.

"I take

生成的文本看起来不错 - 但仔细观察会发现它不是很连贯。3-gramsnew hand sense 和 local batte harness 非常奇怪，看起来不像是人写的。这就是对单词序列进行采样时的大问题: 模型通常会产生不连贯的乱码，参见​Ari Holtzman 等人 (2019) 的论文。

缓解这一问题的一个技巧是通过降低所谓的 softmax 的“温度”使分布 $P(w|w_{1:t-1})$ 更陡峭。而降低“温度”，本质上是增加高概率单词的似然并降低低概率单词的似然。将温度应用到于我们的例子中后，结果如下图所示。

$t=1$ 时刻单词的条件分布变得更加陡峭，几乎没有机会选择单词 $\text{“car”}$ 了。

# set seed to reproduce results. Feel free to change the seed though to get different results
tf.random.set_seed(0)

# use temperature to decrease the sensitivity to low probability candidates
sample_output = model.generate(
    input_ids, 
    do_sample=True, 
    max_length=50, 
    top_k=0, 
    temperature=0.7
)

print("Output:\n" + 100 * '-')
print(tokenizer.decode(sample_output[0], skip_special_tokens=True))

Output:
----------------------------------------------------------------------------------------------------
I enjoy walking with my cute dog, but I don't like to be at home too much. I also find it a bit weird when I'm out shopping. I am always away from my house a lot, but I do have a few friends

奇怪的 n-gram 变少了，现在输出更连贯了！虽然温度可以使分布的随机性降低，但极限条件下，当“温度”设置为 $0$ 时，温度缩放采样就退化成贪心解码了，因此会遇到与贪心解码相同的问题。

Top-K 采样

Fan 等人 (2018) 的论文介绍了一种简单但非常强大的采样方案，称为 Top-K 采样。在 Top-K 采样中，概率最大的 K 个词会被选出，然后这 K 个词的概率会被重新归一化，最后就在这重新被归一化概率后的 K 个词中采样。 GPT2 采用了这种采样方案，这也是它在故事生成这样的任务上取得成功的原因之一。

我们将上文例子中的候选单词数从 3 个单词扩展到 10 个单词，以更好地说明 Top-K 采样。

设 $K = 6$，即我们将在两个采样步的采样池大小限制为 6 个单词。我们定义 6 个最有可能的词的集合为 $V_{\text{top-K}}$。在第一步中，$V_{\text{top-K}}$ 仅占总概率的大约三分之二，但在第二步，它几乎占了全部的概率。同时，我们可以看到在第二步该方法成功地消除了那些奇怪的候选词 $(\text{“not”}, \text{“the”}, \text{“small”}, \text{“told”})$。现在还有一个问题，Top-K 采样不会动态调整从需要概率分布 $P(w|w_{1:t-1})$ 中选出的单词数。这可能会有问题，因为某些分布可能是非常尖锐 (上图中右侧的分布)，而另一些可能更平坦 (上图中左侧的分布)，所以对不同的分布使用同一个绝对数 K 可能并不普适。在 $t=1$ 时，Top-K 将 $(\text{“people”}, \text{“big”}, \text{“house”}, \text{“cat”})$ 排出了采样池，而这些词似乎是合理的候选词。另一方面，在$t=2$ 时，该方法却又把不太合适的 $(\text{“down”}, \text{“a”})$ 纳入了采样池。因此，将采样池限制为固定大小 K 可能会在分布比较尖锐的时候产生胡言乱语，而在分布比较平坦的时候限制模型的创造力。这一发现促使 Ari Holtzman 等人 (2019) 发明了 Top-p- 或 核- 采样。

Top-p (核) 采样

在 Top-p 中，采样不只是在最有可能的 K 个单词中进行，而是在累积概率超过概率 p 的最小单词集中进行。然后在这组词中重新分配概率质量。这样，词集的大小 (又名 集合中的词数) 可以根据下一个词的概率分布动态增加和减少。好吧，说的很啰嗦，一图胜千言。

假设 $p=0.92$，Top-p 采样对单词概率进行降序排列并累加，然后选择概率和首次超过 $p=0.92$ 的单词集作为采样池，定义为 $V_{\text{top-p}}$。在 $t=1$ 时 $V_{\text{top-p}}$ 有 9 个词，而在 $t=2$ 时它只需要选择前 3 个词就超过了 92%。其实很简单吧！可以看出，在单词比较不可预测时，它保留了更多的候选词，如 $P(w | \text{“The”})$，而当单词似乎更容易预测时，只保留了几个候选词，如 $P(w | \text{“The”}, \text{“car”})$。

‍