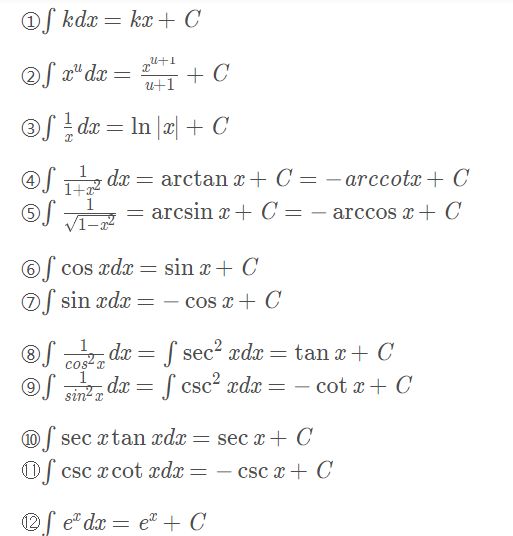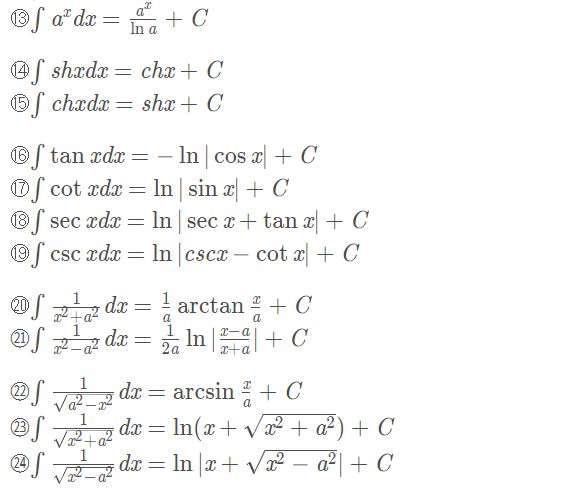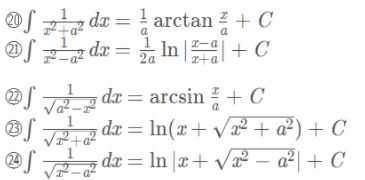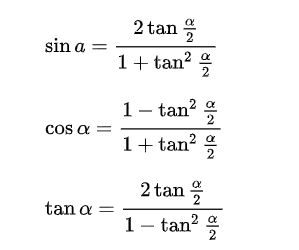高等数学不定积分
目录
（一）背诵基本积分公式
（二）换元积分法
（1）换元准则:
（2） 第一类换元积分法（将d前的部分函数转化为原函数后替代掉d后的自变量x，凑出d内外自变量一致后，利用积分表）
（3）第二类换元积分法
（4）分部积分法
（三）有理函数的积分
（一）背诵基本积分公式
---------------------------------------------------------------------------------------------------------
（二）换元积分法
（1）换元准则:
（1）d前后移原函数，d后前移导函数；
（2）d后可以加减任意常数不影响结果（方便配凑后直接利用积分表，只有d内外自变量一致时才能说某函数对应某自变量求原函数）；
（3）d前后有任意与函数相乘的常数都可将其提取出去；
--------------------------------------------------------------------------------------
（2） 第一类换元积分法（将d前的部分函数转化为原函数后替代掉d后的自变量x，凑出d内外自变量一致后，利用积分表）
(1) 积化和差，和差化积公式有利于化简后使用第一类换元积分
例1 
（2） 有时需要同时转化多个元素成为原函数
例1 
（3） 能优先消参就优先消参
例1 
（4） 记忆一些常用函数的原函数利于使用分部积分法时提入分部
例1 
例2 
（5）能换成同次幂的x就优先用第一类换元法
例1 
（6）高次三角函数题（奇次幂利用第一类化为偶次幂，偶次幂利用2sinxcox=sin2x或降幂公式来进行降次，最终都要将
的形式转为sinnx的形式后用第一类换元法）
例1 
例2 
拆分成两部分，左侧利用积分表，右侧利用第一类积分法（虽然形似第二类，但是能够内外同次幂x就不必用第二类换元法）；
--------------------------------------------------------------------------------------
（3）第二类换元积分法
（将d后的函数求导后移入d前使得dt变为dx）（多数情况下利用其来解含根号的积分题）
（1） a^2与x^2的纠缠类，可以参考积分表；
（对这类格式的题配凑出一对的x^2与a^2后格式正确直接利用这些公式会很方便）
例1 
2 三角函数换元法：利用三角函数来替代x，能够使
替换为一个三角函数来实现去根的目的；（一般的，使用三角函数换元法时，利用sin^2+cos^2=1与set^2=1+tan^2与csc^2=cot^2+1两公式来合理的替换成三角函数；);
例1 
例2 
3 设t法：以上解法都不能实现去根时利用换元法设t求解；
例1 
例2 
例3 ![\int \frac{1}{\sqrt{x}\left ( 1+\sqrt[3]{x} \right )}dx](http://img.e-com-net.com/image/info8/5c9934003e7347689d9b682800fcb1ea.png){kind=small}
例4 ![\int \frac{1}{1+\sqrt[3]{x+2}}dx](http://img.e-com-net.com/image/info8/078f9ecc63334685ada210b35016c18f.png){kind=small}
例5 ![\int \frac{dx}{\sqrt[3]{\left ( x+1 \right )^2\left ( x-1 \right )^4}}](http://img.e-com-net.com/image/info8/885df7a57b96467e9465008d036bb4ed.png){kind=small}
例外 ![\int \frac{2x+2}{\sqrt[4]{x^2+2x+7}}dx](http://img.e-com-net.com/image/info8/a7adc441e95946bb88e2e76dfef26d25.png){kind=small}
和
（有的题不需要消根，直接利用第一类换元法就可以求解） ；
--------------------------------------------------------------------------------------
（4）分部积分法
（
）(多用于多式乘积的积分题)
(一) 分部准则
（1） e^x>三角函数>x^n
（2）形如反三角函数，对数函数这些原函数未知或难知的一般不会成为分部
（3）如果分部正确的话，式子应该原来原简便，例如f(x)^n的次幂越来越小）
（二）题型
（1）三角函数转换法:出现三角函数多次幂的形式，可以考虑将其降幂或者替换成其他三角函数（方便成为分部）
（一般d左侧函数转后的形式为sec^2x,csc^2x,secxtanx,cscxcotx,总的来说不能是tanx，cotx形式）
例1 
（利用
） 转化为sec^2x后易求原函数 ）
（2）降幂法：通过降幂达到化简式子易于利用一二类积分法的目的（不把其移入分部则会降幂）
例1 
(将其化为cos4x的形式后利用第一类换元法)
例2 
（让x^2变为x^0）
例3 
(3) 循环法：通过多次对sinx或cosx这种导函数是循环更替的函数进行分部积分法来让后续的计算中再次出现原式,但会有一个常客一直进入分部；
例1 
（常客为e^x）
例2 
（常客为1）
例3 
（常客为1）
-------------------------------------------------------------------------------------------------------------------------------
（三）有理函数的积分
前提 ：分式应该化为真分式；
（1）分式的分母如果是乘积的形式可以利用待定系数法分解为小分式求解
待定系数法：
1. 小分式的上部的式子只看小分式分母中x的最高次幂
2. 小分式的数量由大分式分母中式子乘积的最高次幂决定（如
要分解为
，
,
例1 
例2 
例外1 
（分母为两式子相乘时，两式相减等于分子或是一个常数时可以直接使用裂项相消法，更简便）
例外2 
（显然可以通过分子加减常数配凑后利用第一类换元积分法求解）
（2） 分式下部有一次的三角函数一般利用万能公式对tanx进行设t换元
例1 
例2 
（3）通过因式分解或立方和差公式得到乘积形式用待定系数法
例1 