池化、线性、激活函数层

一、池化层

池化运算是深度学习中常用的一种操作，它可以对输入的特征图进行降采样，从而减少特征图的尺寸和参数数量。

池化运算的主要目的是通过“收集”和“总结”输入特征图的信息来提取出主要特征，并且减少对细节的敏感性。在池化运算中，通常有两种常见的操作：最大池化和平均池化。

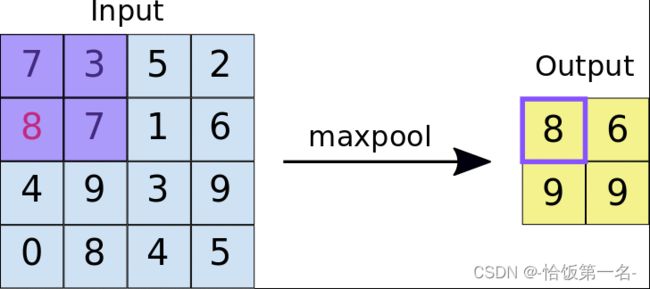
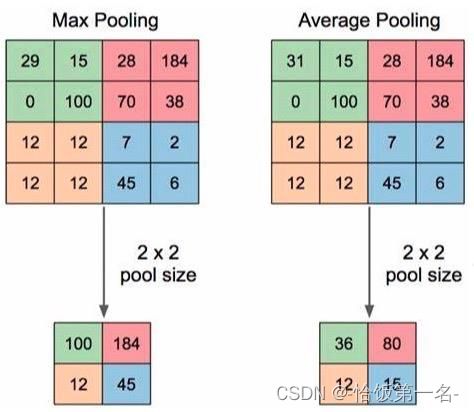
最大池化（Max Pooling）是指在池化窗口内选择最大值作为输出的操作。它可以帮助提取输入特征图中的最显著特征，同时减少了特征图的尺寸。

平均池化（Average Pooling）是指在池化窗口内计算平均值作为输出的操作。它可以对输入特征图进行平滑处理，减少噪声和细节的影响

池化运算通常应用于卷积神经网络的后续层，可以有效地减少特征图的维度，并且具有一定的平移不变性，即对输入的微小平移具有一定的鲁棒性。

总结起来，池化运算通过“收集”输入特征图的信息并进行“总结”，帮助提取主要特征并减少特征图的尺寸。最大池化和平均池化是常见的池化操作，分别选择最大值和平均值作为输出。这些操作在深度学习中被广泛应用于图像识别和计算机视觉任务中。

nn.MaxPool2d

nn.MaxPool2d是PyTorch中用于对二维信号（如图像）进行最大值池化的类。它可以通过选择池化窗口内的最大值来减少特征图的尺寸。

nn.MaxPool2d的主要参数如下：

• kernel_size：池化核尺寸，指定池化窗口的大小。
• stride：步长，指定池化窗口在输入特征图上滑动的步长。默认值为None，表示使用与kernel_size相同的值。
• padding：填充个数，指定在输入特征图周围添加的填充像素数。默认值为0。
• dilation：池化核间隔大小，指定池化核中的元素之间的间距。默认值为1。
• return_indices：是否记录池化像素的索引。如果设置为True，则在池化操作中会返回一个张量，其中包含池化像素的索引。默认值为False。
• ceil_mode：是否向上取整。如果设置为True，则在计算输出特征图的尺寸时会向上取整。默认值为False。

nn.AvgPool2d

nn.AvgPool2d是PyTorch中的一个二维平均池化层，用于对二维信号（如图像）进行平均值池化操作。下面是对主要参数的详细解释：

1. kernel_size（池化核尺寸）：
   • 可以是一个整数，表示池化核的高度和宽度相等。
   • 也可以是一个元组（kH，kW），分别表示池化核的高度和宽度。
2. stride（步长）：
   • 可以是一个整数，表示在高度和宽度上的步长相等。
   • 也可以是一个元组（sH，sW），分别表示在高度和宽度上的步长。
3. padding（填充个数）：
   • 可以是一个整数，表示在输入的每一条边周围填充0的个数。
   • 也可以是一个元组（padH，padW），分别表示在输入的高度和宽度上填充0的个数。
4. ceil_mode（尺寸向上取整）：
   • 一个布尔值，表示是否向上取整输出的尺寸。
   • 如果为False（默认值），则向下取整。
   • 如果为True，则向上取整。
5. count_include_pad（填充值用于计算）：
   • 一个布尔值，表示在计算平均值时是否包括填充值。
   • 如果为True（默认值），则包括填充值。
   • 如果为False，则不包括填充值。
6. divisor_override（除法因子）：
   • 一个整数，用于覆盖默认的除法因子。
   • 如果设置了该参数，则用它来除以池化窗口的总元素数。

nn.AvgPool2d(kernel_size, 
			 stride=None, 
			 padding=0, 
			 ceil_mode=False, 
			 count_include_pad=True, 
			 divisor_override=None)

这些参数可以根据需要进行调整，以控制池化操作的行为。

---

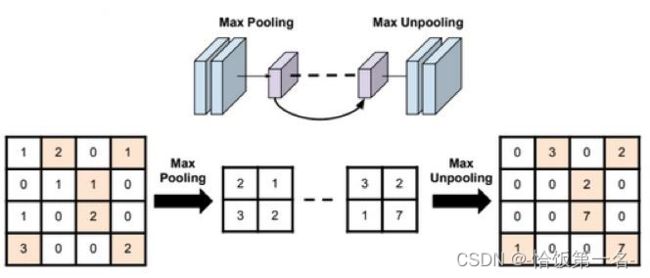
nn.MaxUnpool2d

对二维信号（图像）进行最大值池化和上采样是常用的图像处理操作。在PyTorch中，可以使用nn.MaxPool2d进行最大值池化操作，使用nn.MaxUnpool2d进行上采样操作。下面是对主要参数的详细解释：

1. nn.MaxPool2d（最大值池化）：
   • kernel_size（池化核尺寸）：可以是一个整数或一个元组，表示池化核的高度和宽度。
   • stride（步长）：可以是一个整数或一个元组，表示在高度和宽度上的步长。
   • padding（填充个数）：可以是一个整数或一个元组，表示在输入的每一条边周围填充0的个数。
2. nn.MaxUnpool2d（上采样）：
   • kernel_size（池化核尺寸）：可以是一个整数或一个元组，表示池化核的高度和宽度。
   • stride（步长）：可以是一个整数或一个元组，表示在高度和宽度上的步长。
   • padding（填充个数）：可以是一个整数或一个元组，表示在输入的每一条边周围填充0的个数。
     在进行上采样时，需要使用nn.MaxUnpool2d的forward方法，其中的参数包括：
   • input：输入张量，即经过最大值池化的特征图。
   • indices：最大值池化过程中记录的最大值的索引，用于恢复原始特征图。
   • output_size：输出的尺寸，可以是一个整数或一个元组，表示上采样后的特征图的尺寸。

使用nn.MaxPool2d对图像进行最大值池化，可以提取图像的主要特征。使用nn.MaxUnpool2d进行上采样，可以恢复池化之前的原始特征图尺寸。

---

线性层

我们可以使用矩阵乘法来计算线性层的输出。下面是对计算步骤的详细解释：

1. 输入数据（Input）：
   • 输入数据是一个形状为(1, 3)的张量，表示一组样本，每个样本有3个特征。
   • 输入数据为[1, 2, 3]，可以表示为一个1行3列的矩阵。
2. 权重矩阵（W_0）：
   • 权重矩阵是一个形状为(3, 4)的张量，表示线性层中每个神经元与上一层所有神经元之间的连接权重。
   • 权重矩阵为：
     1 2 3 4
     1 2 3 4
     1 2 3 4
   • 权重矩阵的行数等于输入数据的特征数，列数等于线性层的神经元数。
3. 线性组合（Hidden）：
   • 线性组合可以通过矩阵乘法来实现。将输入数据（Input）与权重矩阵（W_0）相乘，得到线性组合的结果。
   • 矩阵乘法的规则是，输入数据的每一行与权重矩阵的每一列对应元素相乘，然后将乘积相加。
   • 根据计算，线性组合的结果为：
     = [1 * 1 + 2 * 1 + 3 * 1, 1 * 2 + 2 * 2 + 3 * 2, 1 * 3 + 2 * 3 + 3 * 3, 1 * 4 + 2 * 4 + 3 * 4]
     = [6, 12, 18, 24]

因此，根据给定的输入数据和权重矩阵，线性层的输出为[6, 12, 18, 24]。

nn.Linear

nn.Linear是PyTorch中的线性层（全连接层）模块，用于对一维信号（向量）进行线性组合。下面是对主要参数的详细解释：

1. in_features（输入结点数）：
   • 一个整数，表示输入向量的维度（结点数）。
   • 输入向量的形状应为(batch_size, in_features)。
2. out_features（输出结点数）：
   • 一个整数，表示输出向量的维度（结点数）。
   • 输出向量的形状为(batch_size, out_features)。
3. bias（是否需要偏置）：
   • 一个布尔值，表示是否在线性组合中使用偏置。
   • 如果为True，则线性组合的计算公式为：y = + 。
   • 如果为False，则线性组合的计算公式为：y = 。

在使用nn.Linear时，输入向量会与权重矩阵进行矩阵乘法运算，然后加上偏置（如果bias为True）。最终得到输出向量。

例如，如果输入向量的形状为(batch_size, in_features)，权重矩阵的形状为(in_features, out_features)，偏置的形状为(out_features,)，则输出向量的形状为(batch_size, out_features)。

激活函数层

激活函数对特征进行非线性变换，赋予多层神经网络具有深度的意义

1. 描述了一个多层神经网络的计算过程，其中表示输入特征，、、表示权重矩阵，、表示隐藏层的输出，O表示神经网络的输出。
2. 在这个计算过程中，每一层的输出都是通过将输入特征与对应的权重矩阵相乘得到的。这种线性组合的过程只能对特征进行线性变换，无法处理非线性的关系。为了赋予神经网络更强的表达能力，需要引入激活函数对特征进行非线性变换。
3. 激活函数的作用是将线性组合的结果进行非线性映射，从而引入非线性关系。常用的激活函数包括ReLU、Sigmoid、Tanh等。将激活函数应用于每一层的输出，可以增加神经网络的表达能力，使其能够学习更复杂的模式和关系。
4. 根据提供的公式，可以将其表示为 ∗ ，其中表示整个多层神经网络的权重矩阵，包括、、。这个公式表达了多层神经网络对输入特征进行线性组合和非线性变换的过程。

---

nn.Sigmoid

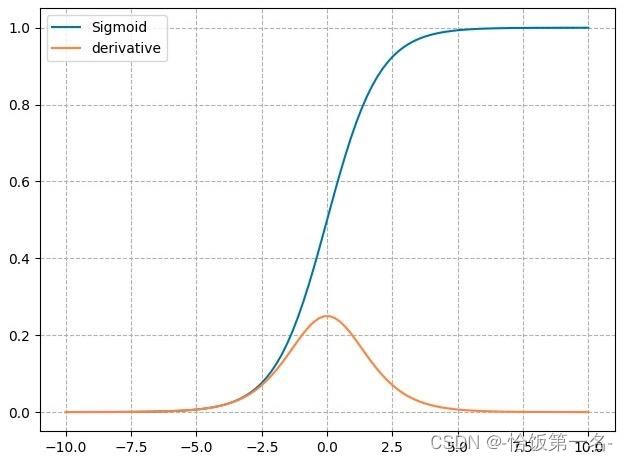
nn.Sigmoid是PyTorch中的Sigmoid激活函数模块，用于对输入进行非线性变换。下面是对Sigmoid激活函数的特性的详细解释：

1. 计算公式：
   • Sigmoid激活函数的计算公式为： = 1 / (1 + ^(-))，其中表示输入。
   • Sigmoid函数将输入映射到一个取值范围在(0, 1)之间的输出。
2. 梯度公式：
   • Sigmoid函数的导数公式为：’ = * (1 - )，其中表示Sigmoid函数的输出。
   • Sigmoid函数的导数范围在[0, 0.25]之间。
   • 这意味着在反向传播过程中，梯度会逐渐减小，容易导致梯度消失的问题。
3. 特性：
   • 输出值在(0, 1)之间，符合概率的范围。
   • Sigmoid函数的导数范围较小，容易导致梯度消失的问题，尤其在深层神经网络中。
   • 输出为非0均值，这可能会破坏数据的分布特性，导致训练不稳定。

由于Sigmoid函数的导数范围较小，容易导致梯度消失的问题，在深层神经网络中，通常会选择其他的激活函数，如ReLU、LeakyReLU等，以解决梯度消失的问题。

nn.tanh

nn.tanh是PyTorch中的tanh激活函数模块，用于对输入进行非线性变换。下面是对tanh激活函数的特性的详细解释：

1. 计算公式：
   • tanh激活函数的计算公式为： = (^ - ^(-)) / (^ + ^(-))，其中表示输入。
   • tanh函数将输入映射到一个取值范围在(-1, 1)之间的输出。
2. 梯度公式：
   • tanh函数的导数公式为：’ = 1 - ^2，其中表示tanh函数的输出。
   • tanh函数的导数范围在(0, 1)之间。
   • 这意味着在反向传播过程中，梯度会逐渐减小，容易导致梯度消失的问题。
3. 特性：
   • 输出值在(-1, 1)之间，数据符合0均值的特性。
   • tanh函数的导数范围较小，容易导致梯度消失的问题，尤其在深层神经网络中。

与Sigmoid函数类似，由于tanh函数的导数范围较小，容易导致梯度消失的问题，在深层神经网络中，通常会选择其他的激活函数，如ReLU、LeakyReLU等，以解决梯度消失的问题。

---

nn.ReLU

ReLU（Rectified Linear Unit）是一种常用的激活函数，它在深度学习中广泛应用。它的计算公式为 = max(0, )，其中是输入，是输出。

ReLU的梯度公式为：
’ = 1, > 0
’ = 0, ≤ 0

ReLU的特性如下：

1. 输出值均为正数，负半轴导致死神经元：当输入大于0时，ReLU的输出为，保持正数；当输入小于等于0时，ReLU的输出为0，将负数归零。这种特性可以使神经网络更好地处理正数输入。
2. 导数是1，缓解梯度消失，但易引发梯度爆炸：当输入大于0时，ReLU的导数为1，保持梯度不变，有助于缓解梯度消失问题；但当输入小于等于0时，ReLU的导数为0，梯度完全消失。这也意味着ReLU在反向传播过程中可能会遇到梯度爆炸的问题。

总的来说，ReLU是一种简单且有效的激活函数，在深度学习中被广泛使用。它能够提供非线性变换，且计算简单高效。然而，ReLU的负半轴导致的死神经元问题和梯度爆炸问题需要注意。为了解决这些问题，后续还出现了一些改进的激活函数，如Leaky ReLU、PReLU等。

---

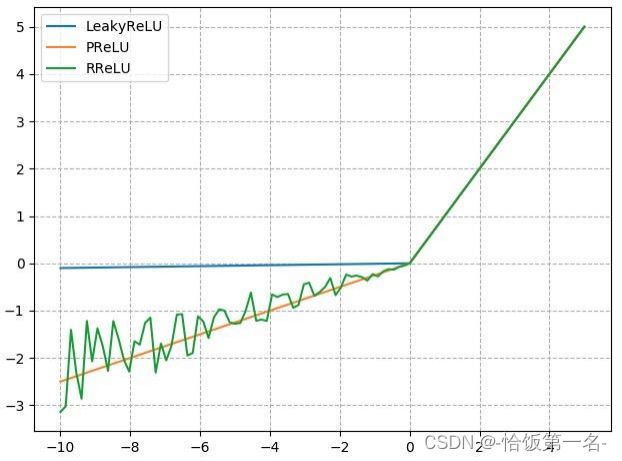
nn.LeakyReLU

nn.LeakyReLU是一种改进的激活函数，它在ReLU的基础上引入了一个负半轴斜率参数。其计算公式为：
= max(, _ * )
其中，是输入，是输出，_是负半轴斜率。

nn.PReLU

nn.PReLU是一种带有可学习斜率的激活函数，它在每个神经元上引入了一个学习参数。其计算公式为：
= max(0, ) + * min(0, )
其中，是输入，是输出，是可学习的斜率参数。

nn.RReLU

nn.RReLU是一种带有随机均匀分布斜率的激活函数，它在每个训练样本中引入了一个随机斜率。其计算公式为：
= max(, ) + (, - ) * ( - )
其中，是输入，是输出，是均匀分布下限，是均匀分布上限，(, )是在[, ]范围内的随机数。

这些改进的激活函数在某些情况下可以更好地处理负半轴的输入，从而缓解死神经元问题。它们的引入可以提高神经网络的性能和学习能力。