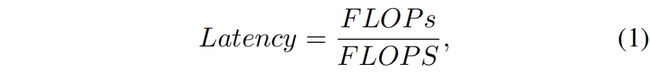FasterNet(CVPR 2023)论文解读
paper:Run, Don't Walk: Chasing Higher FLOPS for Faster Neural Networks
official implementation:https://github.com/jierunchen/fasternet
存在的问题
为了设计轻量、速度快的网络,许多工作都专注于减少floating-point operations (FLOPs)。但FLOPs的减少并不一定意味着相同水平延迟latency的减少。主要原因在于low floating-point operations per second (FLOPS)。
本文的创新点
为了实现更快的网络,本文重新研究了常用的operator并证明了这种low FLOPS主要是算子的频繁内存访问frequent memory access导致的,尤其是深度卷积depthwise convolution。
因此,本文提出了一种新的partial convolution (PConv),通过同时减少冗余的计算和内存访问,更高效的提取空间特征。基于Pconv,本文进一步提出了FasterNet,一种新的神经网络家族。它在各种设备上获得了比其它网络更快的运行速度,同时又没有影响在各种视觉任务上的准确性。
前言
许多轻量网络的设计初衷是为了减少FLOPs,但这些“fast”网络是否真的快?为了回答这个问题,首先需要研究延迟和FLOPs之间的关系
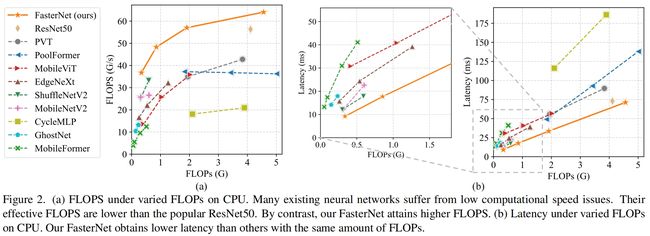
其中FLOPS是floating-point operations per second的缩写,虽然有很多工作是为了减少FLOPs,但它们很少同时考虑优化FLOPS以获得真正的低延迟。为了更好的理解这种情况,作者比较了一些常见的神经网络在Intel CPU上的FLOPS,如图2所示
从图中可以看出,许多网络的FLOPS都比较低,很多低于ResNet50,这种情况下,这些所谓"fast"的网络实际上并不够快。它们在FLOPs上的降低并不能转化为延迟的降低,有些情况下,延迟不光没有改善甚至更高了。例如,CycleMLP-B1的FLOPs是ResNet50的一半,但速度更慢(116.1ms vs. 73.0ms),这种现象在之前的工作中也有提到(如ShuffleNet v2和Mobilevit)但仍然没有解决部分原因是它们使用了DWConv、GConv和各种数据操作,这些都导致了低FLOPS。
Design of PConv and FasterNet
Preliminary
DWConv是Conv的一种变体,已经被广泛用于各种网络中。对于输入 \(\mathbf{I}\in \mathbb{R}^{c\times h\times w}\),DWConv利用 \(c\) 个卷积 \(\mathbf{W}\in \mathbb{R}^{k\times k}\) 得到输出 \(\mathbf{O}\in \mathbb{R}^{c\times h\times w}\)。如图1(b)所示,每个filter在一个输入通道上滑动得到一个输出通道,这使得DWConv的FLOPs为 \(h\times w\times k^{2}\times c\) 相比于普通卷积 \(h\times w\times k^{2}\times c^{2}\) 更少。虽然可以有效减少FLOPs,但DWConv通常后接一个PWConv不能直接用来替代一个普通卷积,因为这会导致精度的显著下降。实际应用中,通常增加DWConv的通道数 \(c'\) (\(c'>c\)) 来补偿精度下降,例如在inverted residual block中通道数增大到了6倍。然而,这会导致内存访问的增加,带来无法忽略的延迟,继而减慢整个计算过程,特别是对于I/O-bound设备。具体现在内存访问次数增加到了
大于普通卷积的内存访问次数,即
注意 \(h\times w\times 2c'\) 的内存访问耗费在I/O操作上,这已经是最小的成本了并且很难进一步优化。
Partial convolution as a basic operator
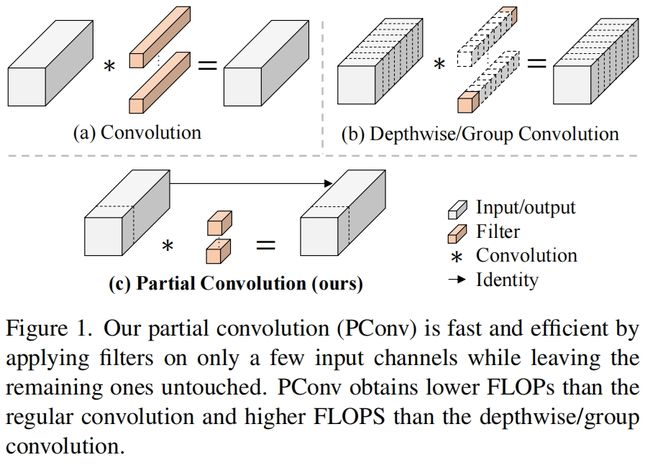
接下里作者展示了如何利用特征图的容易进一步优化成本。如图3所示,这些特征图在不同的通道之间具有很高的相似性,这在之前的研究如Ghostnet中也提出了,但没有以一种简单有效的方式充分利用。本文提出了一种见得PConv来同时减少计算冗余和内存访问,如图4左下所示
它只对输入的部分通道应用普通卷积来提取空间特征,其余通道保持不变。为了连续的内存访问,我们只采用第一个或最后一个连续 \(c_{p}\) 个通道作为计算整个特征映射的代表。在不丧失一般性的情况下,我们只考虑输入和输出特征映射具有相同数量的通道的情况。因此,一个PConv的FLOPs只有
当采用常用的取值 \(r=\frac{c_{p}}{c}=\frac{1}{4}\) 时,一个PConv的FLOPs是一个普通Conv的 \(\frac{1}{16}\)。此外PConv的内存访问也更少
当 \(r=\frac{1}{4}\) 时只有普通卷积的 \(\frac{1}{4}\)。
由于只有 \(c_{p}\) 通道用于空间特征提取,可能有人会问能否直接去掉剩余的 \((c-c_{p})\) 个通道?这样的话,PConv就变成了一个通道更少的普通卷积,这就背离了我们想要减少冗余的初衷。这里我们保留剩余的通道不变而不是直接删除,是因为这对于后续的PConv层有用,它是的特征信息可以流过所有通道。
PConv followed by PWConv
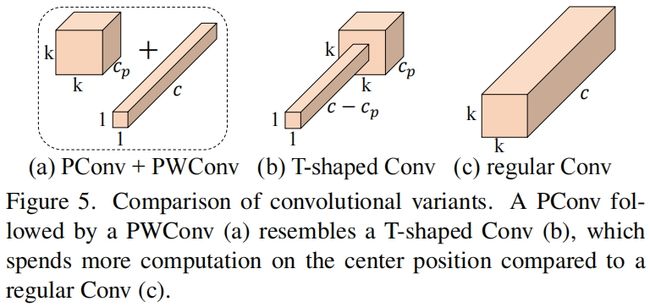
为了充分而高效的利用来自所有通道的信息,作者在PConv的后面添加了一个PWConv。这两个结合起来在输入上的有效感受野看起来像一个T-shaped Conv,如图5所示,与普通卷积相比它更关注于中心区域。
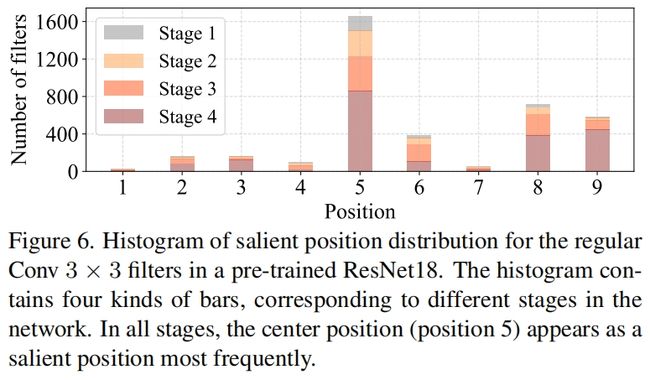
为了证明这种T型感受野,我们通过计算position-wise Frobenius norm来评估每个位置的重要性。我们认为如果一个位置的Frobenius norm比其它位置都大,那么它往往更重要。对于一个普通卷积 \(\mathbf{F}\in \mathbb{R}^{k^{2}\times c}\),位置 \(i\) 处的Frobenius norm通过 \(\left \| \mathbf{F_{i}} \right \| =\sqrt{ {\textstyle \sum_{j=1}^{c}\left | f_{ij} \right |^{2} } },i=1,2,3...,k^{2} \) 计算得到。我们认为一个显著的位置是具有最大Frobenius norm的位置。作者首先研究pretrained ResNet18中的每个卷积核,找到每个卷积核的显著位置,然后画了一个显著位置的直方图,如图6所示,可以看出中心位置作为最显著位置的频率是最高的。换句话说,中心位置的权重比周围都要大,这与T型计算集中于中心处是一致的。
尽管T型卷积可以直接用于高效计算,但作者表示将它分解成一个PConv和一个PWConv更好,因为利用了卷积核之间的冗余进一步减低了FLOPs。对于同样的输入 \(\mathbf{I}\in \mathbb{R}^{c\times h\times w}\) 和 \(\mathbf{O}\in \mathbb{R}^{c\times h\times w}\),一个T型卷积的FLOPs计算如下
这大于一个PConv和一个PWConv的FLOPs
其中 \((k^{2}-1)c>k^{2}c_{p}\),例如当 \(c_{p}=\frac{c}{4},k=3\) 时。此外我们还可以直接利用普通卷积来进行分解后两步的实现。
FasterNet as a general backbone
基于PConv和PWConv,作者进一步提出了FasterNet,一个新的神经网络家族。它的运行速度更快,对许多视觉任务都非常有效。
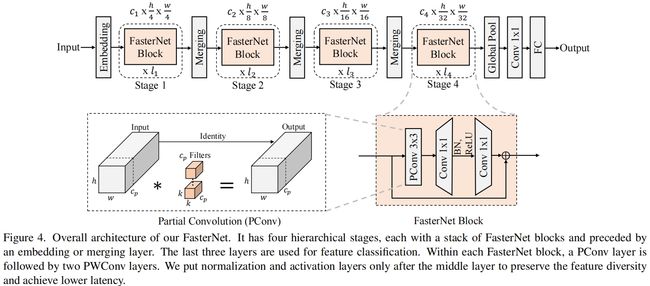
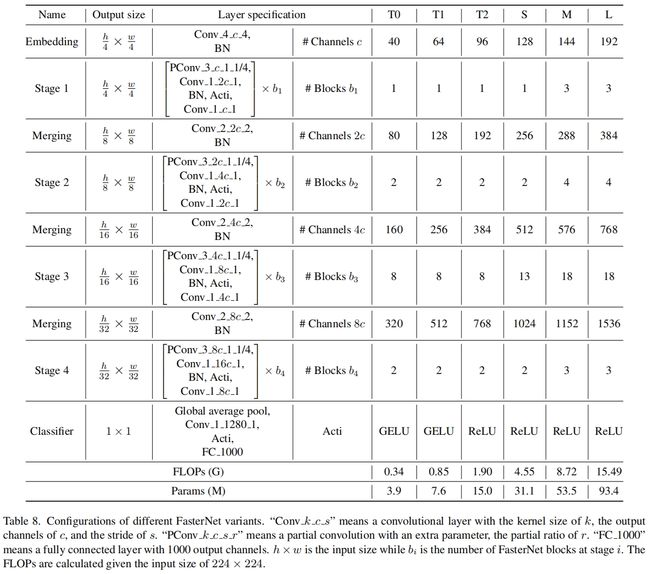
完整的结构如图4所示,它包含4个stage,每个stage之前都有一个embedding layer(一个stride=4的普通卷积)或一个merging layer(一个stride=2的普通卷积)用于下采样或增加通道数。每个stage都包括若干FasterNet blocks。作者发现后两个stage中的block内存访问更少FLOPS更大,因此把更多的block即更多的计算放到后两个stage中。每个block都包括一个PConv层后接两个PWConv(或1x1 Conv)。整理看起来有点像inverted residual block,中间层的通道数更多,还有一个shortcut connection用于特征重用。
除了上述算子,归一化层和激活层对于高性能的神经网络也必不可少。但是很多之前的网络过度使用这些层,这限制了特征的多样性,损害了整体性能,还减慢了计算。相反,本文只在每个中间PWConv之间添加归一化层和激活层来保持特征的多样性并获得更低的延迟。此外本文的归一化层使用BN,因为相比于其它归一化层它可以与相邻的卷积层融合到一起来加快推理。对于激活函数,较小的网络采用GELU,较大的采用ReLU。最后三层,一个全局平均池化,一个1x1卷积,一个全连接层用于特征转换和分类。为了适应不同的计算场景,本文提供了tiny、small、medium、large版本,它们的结构是一致的,只在深度和宽度方面有区别。具体如下
实验结果
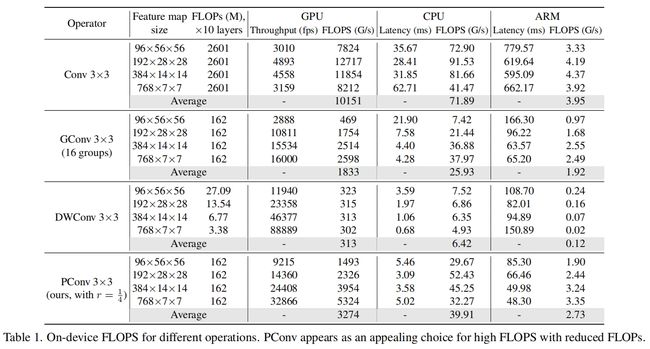
表1展示的是相同规格下10层各类型卷积在不同设备上的FLOPS对比,可以看出PConv的FLOPS是最大的,表明其速度是最快的。
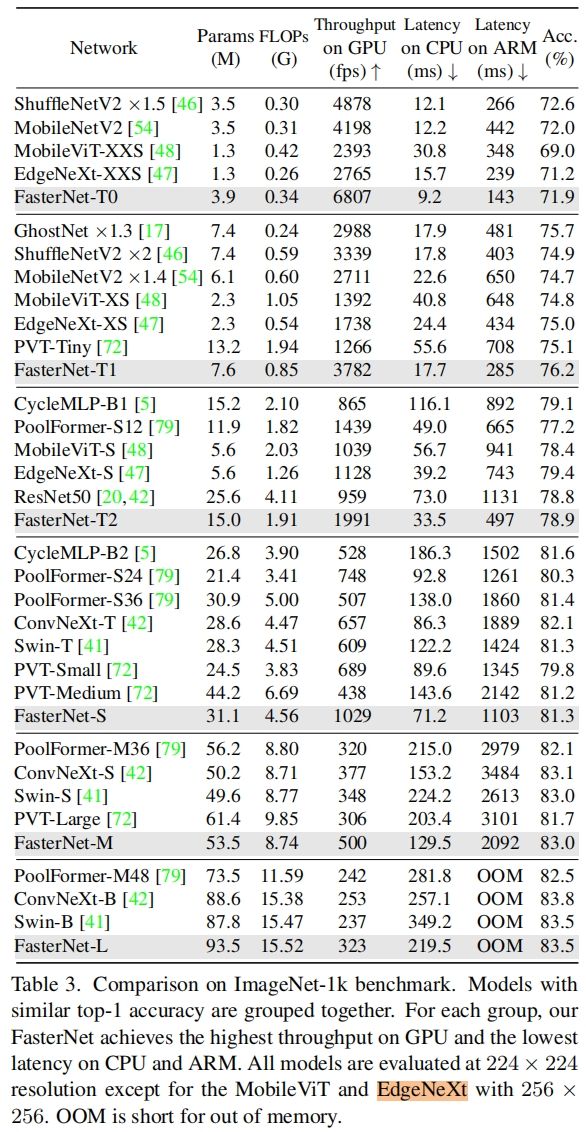
表3是FasterNet和其它SOTA分类模型在ImageNet-1k验证集上的效果,可以看出FasterNet的延迟是最低的
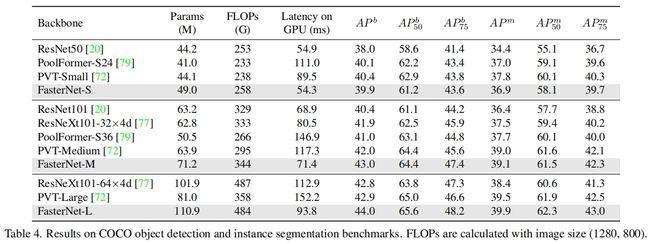
在下游目标检测和实例分割任务上,FasterNet的效果也很好,其中网络结构选择Mask R-CNN