带修莫队 P1903 题解

$\text{Part \# 0. 前言}$

这个蒟蒻刚学带修莫队，所以 介绍带修莫队的部分比较简略，大家可以去参考一下 OI-wiki 或者其他大佬的博客：）

本文参考了洛谷题解。

$\text{Part \# 1. 带修莫队}$

带修莫队，顾名思义，就是待修改的莫队。

众所周知，普通莫队可以在比较好的时间复杂度内完成一次查询操作，但是不支持修改操作，于是就有了带修莫队。

我们知道，莫队实际上是从[l,r]到[l+1,r]、[l-1,r]、[l,r+1]、[l,r-1]的转移，而且都是$O(1)$的，所以如果我们把中括号改成小括号，那么就是莫队的本质了：
(l,r)->(l-1,r)(l+1,r)(l,r-1)(l,r+1)

图中四个箭头的移动都是可以$O(1)$完成的，那么两点之间的曼哈顿距离就是从一个状态到另一个状态所需要的最小挪动

（不了解曼哈顿距离的同学戳上面加粗字体）

那么对于所有的查询，最快的办法就是在坐标系上找到曼哈顿最小生成树

（其实没有必要会这个因为太麻烦了）

你也许会说：“我不会啊！”

这完全没有关系，因为

我也不会

但是我们并没有必要得到最佳答案，能卡过去就够了。

于是我们采用分块的想法，将其分成(n/sz)个长度为sz的块，在每一个块中按照右端点从小到大来移动

就像这样：

至少这样不会被卡掉……

至于块的大小？$\sqrt{n}$呗。

（实际上严谨的说，应该是$\frac{n}{\sqrt{m}}$，具体为啥有兴趣的同学可以研究一下，一般来说块的大小$\sqrt{n}$足矣，因此不在此介绍）

那么我们就讲好了本题……的前置部分……

好了！现在我们在这里加入了修改，“我该怎么办呢qwq”

可以这么认为，序列的值是随着时间而变化的

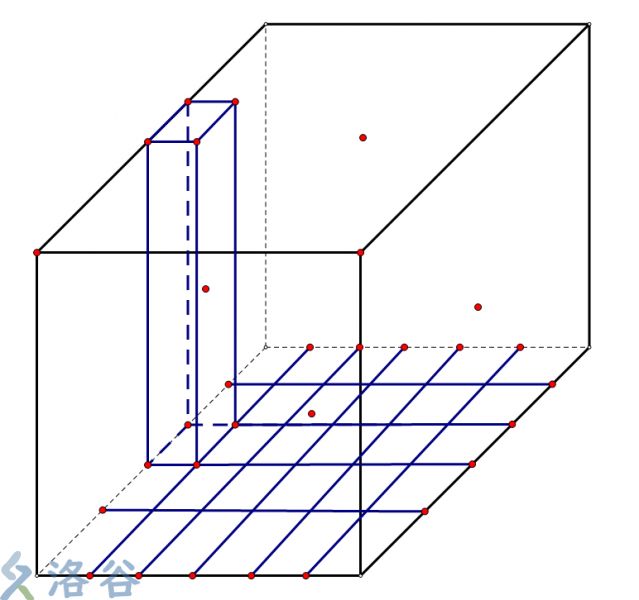
那我们就在坐标系上再加上一个时间维度，用(l,r,t)来表示一个查询

↑大概就是这样

很明显，我们需要分别按照l与r分块，在同一块内的询问按照t从小到大完成。块的大小就是$\sqrt[3]{n^2}=n^{\mathrm{0.6666...}}$

（至于为什么还是看别的题解吧，窝太菜廖）

所以总的来说，只需要在原有的普通莫队上在加一个时间维度就可以了

---

$$\text{Code}$$

/*
1. sqrt(m*2/3)
*/
#include 

using namespace std;

#define int long long
#define fi first
#define se second
#define rg register
#define il inline
#define forz(i,a,b) for(register int i((a));i<=(b);++i)
#define forn(i,a,b) for(register int i((a));i>=(b);--i)
#define IOS ios::sync_with_stdio(0),cin.tie(0),cout.tie(0)

inline int read()
{
	int x=0,f=1;
	char ch=getchar();
	while (ch<'0'||ch>'9') {if(ch=='-') f=-1;ch=getchar();}
	while (ch>='0'&&ch<='9') {x=(x<<3)+(x<<1)+ch-'0';ch=getchar();}
	return x*f;
}

inline void write(int x)
{
    if(x<0){putchar('-');x=-x;}
    if(x>9) write(x/10);
    putchar(x%10+'0');
}

const int maxn=2e5+100;
const int mod=993244853;
const int inf=9e18;

int n,m;
int sum;
int sz;
int cntq,cntr;

struct question{
	int l;
	int r;
	int t;
	int id;
}qq[maxn],qr[maxn];

int a[maxn];
int ans[maxn];
int cnt[maxn*10];

inline void add(int x)
{
	sum+= !cnt[x]++;
}

inline void del(int x)
{
	sum-= !--cnt[x];
}

inline void upd(int x,int t)
{
	if(qq[x].l<=qr[t].l&&qr[t].l<=qq[x].r)
	{
		del(a[qr[t].l]);
		add(qr[t].r);
	}
	swap(a[qr[t].l],qr[t].r);
}

bool cmp (const question &a, const question &b)
{
	return a.l / sz == b.l / sz ? a.r / sz == b.r / sz ? a.t < b.t : a.r < b.r : a.l < b.l;
}

inline void solve()
{
	n=read(),m=read();
	sz=pow(n,0.666);
	forz(i,1,n) a[i]=read();
	forz(i,1,m)
	{
		char op;cin>>op;
		int l=read(),r=read();
		if(op=='Q')
		{
			cntq++;
			qq[cntq].id=cntq;
			qq[cntq].l=l;
			qq[cntq].r=r;
			qq[cntq].t=cntr;
		}
		else
		{
			cntr++;
			qr[cntr].l=l;
			qr[cntr].r=r;
		}
	}	
	sort(qq+1,qq+1+cntq,[](const question &a,const question &b){
		return a.l/sz==b.l/sz?a.r/sz==b.r/sz?a.t<b.t:a.r<b.r:a.l<b.l;
	});
	int L=1,R=0,T=0;
	forz(i,1,cntq)
	{	
		while (L>qq[i].l) add(a[--L]);
		while (L<qq[i].l) del(a[L++]);
		while (R>qq[i].r) del(a[R--]);
		while (R<qq[i].r) add(a[++R]);
		while (T<qq[i].t) upd(i,++T);
		while (T>qq[i].t) upd(i,T--);
		ans[qq[i].id]=sum;
	}
	forz(i,1,cntq)
	{
		write(ans[i]);
		putchar('\n');
	}
	putchar('\n');
}

signed main()
{
//    IOS;
	int _=1;
	while (_--) solve();
	return 0;
}