理论U2 贝叶斯决策理论

一、概率统计理论基础

1、乘法公式

设A，B为任意事件，$P(A,B)=P(A|B)\ast P(B)=P(B|A)\ast P(A)$

2、全概率公式

设$A_1,A_2,\dots ,A_n$两两互不相容，且$B$的发生总是与$A_1,A_2,\dots ,A_n$之一同时发生，则对于事件$B$，有：
$P(B)={\sum }_{k-1}^{n}P(A_k)P(B|A_k)$

3、贝叶斯公式

知因求果
$P(A_k|B)=\frac{P(A_{k}B)}{P(B)}=\frac{P(A_k)P(B|A_k)}{{\sum }_{i-1}^{n}P(A_i)P(B|A_i)}$

贝叶斯公式给出了“结果”事件B已经发生的条件下，“原因”事件A的条件概率，对结果的任何观测都将增加我们对原因事件A的真正分布的知识。

二、贝叶斯决策理论

1、用处

是机器学习/模式分类问题的基本理论之一
用概率统计的观点和方法（基于贝叶斯公式）来解决模式识别问题

2、解决问题

分类问题
给定：m个类、已知类别属性的训练样本和未知类别属性的输入数据
目标：确定每一个输入数据的类别属性

3、决策基础

已知条件：
–类别数一定（决策论中把类别也称为状态） ${\omega }_i,i=1,2,\dots ,c$
–已知各类在这d维特征空间的统计分布
各类别${\omega }_i$ $i=1,2,\dots ,c$的先验概率 $P(x|{\omega }_i)$， i= 1,2,…,c

决策：根据贝叶斯公式计算后验概率 $P({\omega }_i|x)$ ，基于最大后验概率进行判决

4、一些概念

• 样本（sample） $x\in R^d$
• 类别/状态（class/state）$w_i$
• 先验概率（a priori probability or prior）$P(w_i)$
• 样本分布密度（sample distribution density）$p(x)$
• 类条件概率密度（class-conditional probabilitydensity） $p(x|w_i)$
• 后验概率（a posteriori probability or posterior ） $p(w_i|x)$
• 错误概率（probability of error）:

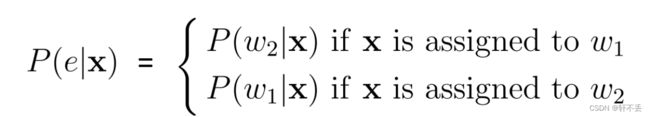
• 平均错误率（average probability of error） $P(e)=\int P(e|x)p(x)dx$
• 正确率（probability of correctness） $P(c)$

5、核心公式

$P(w_i|x)=\frac{P(x|w_i)P(w_i)}{P(x)}=\frac{P(x|w_i)P(w_i)}{{\sum }_i^{c}P(x|w_i)P(w_i)}$
先验概率：由以往历史数据得到的概率
后验概率：利用最新输入数据对先验概率加以修正后的概率
以最大后验概率为判决函数（样本在哪个类别概率大就属于哪个类别）

三、最小错误率贝叶斯决策

1、目标

$minP(e)=\int P(e|x)p(x)dx$

2、例题分析

3、问题

1）决策的风险

不同的决策具有不同的风险或损失。
比如医疗诊断为例：没病判为有病：精神负担、可进一步检查，损失不大。有病判为没病：贻误病情，后果严重。
最小错误率贝叶斯决策以错误率最小为准则，未考虑决策的风险

四、最小风险贝叶斯决策

1、背景

根据最小错误率贝叶斯决策的问题进行改进

2、基本概念

1）损失函数

损失函数：对于特定的x采取决策$\alpha$的期望损失$\lambda ({\alpha }_i,w_j)$

2）条件期望损失：

$R({\alpha }_i|x)=E[\lambda ({\alpha }_i,w_j)]={\sum }_{j=1}^c\lambda ({\alpha }_i,w_j)p(w_j|x)$

3）期望风险：

对所有可能的x采取决策$\alpha (x)$所造成的期望损失之和
$R(\alpha )=\int R(\alpha |x)p(x)dx$

3、目标

$minR(\alpha )=\int R(\alpha |x)p(x)dx$
若对每一个决策，都使其条件风险$R({\alpha }_i|x)$最小，则对所有 x 做出决策时，其期望风险 R 也最小

4、决策

如果 $R({\alpha }_k|x)=minR({\alpha }_i|x)$ ，则$\alpha ={\alpha }_k$

5、算法步骤

6、例题分析

上题的细胞诊断

五、两种贝叶斯的关系

六、朴素贝叶斯决策

1、问题

贝叶斯决策的问题：类条件概率 $P(x|{\omega }_i)$ 是所有属性上的联合概率，难以从有限的训练样本直接估计得到。
因此需要用朴素贝叶斯决策

2、概念

属性条件独立性假设：对于已知类别，假设所有属性相互独立；即假设各属性独立地对分类结果发生影响，
$P(X|w)=P(x_1,x_2,x_3,x_4,...,x_d|w)={\Pi }_{i=1}^{d}P(x_i|w)$

3、例题分析