poj1416——dfs递归枚举+记录路径
POJ 1416 dfs递归枚举+记录路径
Shredding Company
| Time Limit: 1000MS | Memory Limit: 10000K | |
| Total Submissions: 4456 | Accepted: 2555 |
Description
You have just been put in charge of developing a new shredder for the Shredding Company Although a "normal" shredder would just shred sheets of paper into little pieces so that the contents would become unreadable, this new shredder needs to have the following unusual basic characteristics.
1.The shredder takes as input a target number and a sheet of paper with a number written on it.
2.It shreds (or cuts) the sheet into pieces each of which has one or more digits on it.
3.The sum of the numbers written on each piece is the closest possible number to the target number, without going over it.
For example, suppose that the target number is 50, and the sheet of paper has the number 12346. The shredder would cut the sheet into four pieces, where one piece has 1, another has 2, the third has 34, and the fourth has 6. This is because their sum 43 (= 1 + 2 + 34 + 6) is closest to the target number 50 of all possible combinations without going over 50. For example, a combination where the pieces are 1, 23, 4, and 6 is not valid, because the sum of this combination 34 (= 1 + 23 + 4 + 6) is less than the above combination's 43. The combination of 12, 34, and 6 is not valid either, because the sum 52 (= 12 + 34 + 6) is greater than the target number of 50.
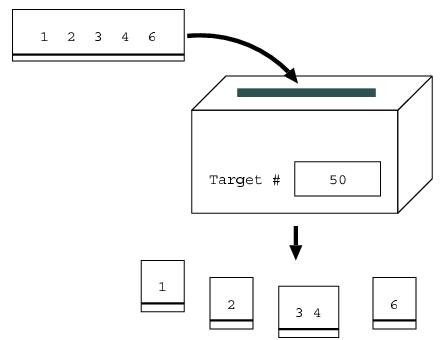
Figure 1. Shredding a sheet of paper having the number 12346 when the target number is 50
There are also three special rules :
1.If the target number is the same as the number on the sheet of paper, then the paper is not cut.
For example, if the target number is 100 and the number on the sheet of paper is also 100, then
the paper is not cut.
2.If it is not possible to make any combination whose sum is less than or equal to the target number, then error is printed on a display. For example, if the target number is 1 and the number on the sheet of paper is 123, it is not possible to make any valid combination, as the combination with the smallest possible sum is 1, 2, 3. The sum for this combination is 6, which is greater than the target number, and thus error is printed.
3.If there is more than one possible combination where the sum is closest to the target number without going over it, then rejected is printed on a display. For example, if the target number is 15, and the number on the sheet of paper is 111, then there are two possible combinations with the highest possible sum of 12: (a) 1 and 11 and (b) 11 and 1; thus rejected is printed. In order to develop such a shredder, you have decided to first make a simple program that would simulate the above characteristics and rules. Given two numbers, where the first is the target number and the second is the number on the sheet of paper to be shredded, you need to figure out how the shredder should "cut up" the second number.
1.The shredder takes as input a target number and a sheet of paper with a number written on it.
2.It shreds (or cuts) the sheet into pieces each of which has one or more digits on it.
3.The sum of the numbers written on each piece is the closest possible number to the target number, without going over it.
For example, suppose that the target number is 50, and the sheet of paper has the number 12346. The shredder would cut the sheet into four pieces, where one piece has 1, another has 2, the third has 34, and the fourth has 6. This is because their sum 43 (= 1 + 2 + 34 + 6) is closest to the target number 50 of all possible combinations without going over 50. For example, a combination where the pieces are 1, 23, 4, and 6 is not valid, because the sum of this combination 34 (= 1 + 23 + 4 + 6) is less than the above combination's 43. The combination of 12, 34, and 6 is not valid either, because the sum 52 (= 12 + 34 + 6) is greater than the target number of 50.

Figure 1. Shredding a sheet of paper having the number 12346 when the target number is 50
There are also three special rules :
1.If the target number is the same as the number on the sheet of paper, then the paper is not cut.
For example, if the target number is 100 and the number on the sheet of paper is also 100, then
the paper is not cut.
2.If it is not possible to make any combination whose sum is less than or equal to the target number, then error is printed on a display. For example, if the target number is 1 and the number on the sheet of paper is 123, it is not possible to make any valid combination, as the combination with the smallest possible sum is 1, 2, 3. The sum for this combination is 6, which is greater than the target number, and thus error is printed.
3.If there is more than one possible combination where the sum is closest to the target number without going over it, then rejected is printed on a display. For example, if the target number is 15, and the number on the sheet of paper is 111, then there are two possible combinations with the highest possible sum of 12: (a) 1 and 11 and (b) 11 and 1; thus rejected is printed. In order to develop such a shredder, you have decided to first make a simple program that would simulate the above characteristics and rules. Given two numbers, where the first is the target number and the second is the number on the sheet of paper to be shredded, you need to figure out how the shredder should "cut up" the second number.
Input
The input consists of several test cases, each on one line, as follows :
tl num1
t2 num2
...
tn numn
0 0
Each test case consists of the following two positive integers, which are separated by one space : (1) the first integer (ti above) is the target number, (2) the second integer (numi above) is the number that is on the paper to be shredded.
Neither integers may have a 0 as the first digit, e.g., 123 is allowed but 0123 is not. You may assume that both integers are at most 6 digits in length. A line consisting of two zeros signals the end of the input.
tl num1
t2 num2
...
tn numn
0 0
Each test case consists of the following two positive integers, which are separated by one space : (1) the first integer (ti above) is the target number, (2) the second integer (numi above) is the number that is on the paper to be shredded.
Neither integers may have a 0 as the first digit, e.g., 123 is allowed but 0123 is not. You may assume that both integers are at most 6 digits in length. A line consisting of two zeros signals the end of the input.
Output
For each test case in the input, the corresponding output takes one of the following three types :
sum part1 part2 ...
rejected
error
In the first type, partj and sum have the following meaning :
1.Each partj is a number on one piece of shredded paper. The order of partj corresponds to the order of the original digits on the sheet of paper.
2.sum is the sum of the numbers after being shredded, i.e., sum = part1 + part2 +...
Each number should be separated by one space.
The message error is printed if it is not possible to make any combination, and rejected if there is
more than one possible combination.
No extra characters including spaces are allowed at the beginning of each line, nor at the end of each line.
sum part1 part2 ...
rejected
error
In the first type, partj and sum have the following meaning :
1.Each partj is a number on one piece of shredded paper. The order of partj corresponds to the order of the original digits on the sheet of paper.
2.sum is the sum of the numbers after being shredded, i.e., sum = part1 + part2 +...
Each number should be separated by one space.
The message error is printed if it is not possible to make any combination, and rejected if there is
more than one possible combination.
No extra characters including spaces are allowed at the beginning of each line, nor at the end of each line.
Sample Input
50 12346 376 144139 927438 927438 18 3312 9 3142 25 1299 111 33333 103 862150 6 1104 0 0
Sample Output
43 1 2 34 6 283 144 139 927438 927438 18 3 3 12 error 21 1 2 9 9 rejected 103 86 2 15 0 rejected
题意:将一个数s按位拆成几个数,使这些数的和最接近目标数t而又不超过t,按要求输出这些数的和以及这些数
这题我干了一下午我也是醉醉的。。。一开始将数拆成前缀和后缀,分别对前缀和后缀进行深搜,然后越弄越麻烦。。看了题解后发现只需搜后缀即可,保留前缀。
题目还要记录路径,由于要搜出所有情况之后才能得到答案,所以不能直接用栈存路径,因为最后栈会被清空,只能拿栈作辅助记录路径,用贪心选择性质,当得到一个更优解时,用另一个数组从栈中保存路径,这里用数组模拟栈,以方便利用memcpy函数直接复制路径,虽然干了一下午才AC,不过0ms过了还是很开心

//poj1416_dfs+记录路径,0ms #include<iostream> #include<cstdlib> #include<cstdio> #include<cstring> #include<algorithm> #include<queue> using namespace std; const int maxn=1000100; const int INF=(1<<28); int s,t; int path[10],cnt; int ans_path[20],ans_cnt; int ans; int down; int mp(int n,int k) { int res=1; while(k--) res*=n; return res; } int digit(int n) { int res=0; if(!n) return 1; while(n){ res++; n/=10; } return res; } void dfs(int n,int L,int sum) { path[cnt++]=n;//数组模拟栈 if(sum<=t){ if(sum>ans){ down=1; ans=sum; memcpy(ans_path,path,sizeof(path)); //用数组模拟栈的优点在这里体现了 ans_cnt=cnt; } else if(sum==ans) down++; } for(int i=1;i<L;i++){ // n为后缀 int k=mp(10,i); int f=n/k,r=n%k; //f为新前缀,r为新后缀 dfs(r,i,sum-n+f+r); } cnt--; } int main() { while(cin>>t>>s,t||s){ if(s==t){ cout<<s<<" "<<s<<endl; continue; } ans=0; down=0; cnt=0; dfs(s,digit(s),s); if(!down) cout<<"error"<<endl; else if(down==1){ cout<<ans; for(int i=0;i<ans_cnt-1;i++) cout<<" "<<ans_path[i]/mp(10,digit(ans_path[i+1])); cout<<" "<<ans_path[ans_cnt-1]<<endl; } else cout<<"rejected"<<endl; } return 0; }
