检索算法: BM25原理详解
文章目录
-
- 简介
- Function
-
- k 1 k_1 k1 的作用
- b b b 的作用
- 终极总结
- 参考文档
简介
BM25算法常用来进行搜索。
输入问题 Q 0 Q_0 Q0,在数据中去匹配其它Q时,可以用BM25进行排序。
"BM"其实就是指Best Matching。
BM25也称Okapi BM25。"Okapi"其实是第一个使用BM25进行检索的系统名字。
Function
BM25其实代表着一个家族。这个家族里的式子互相之间可能会有一些成分、参数的差异,但它们同根同源。
这个家族里最常见的成员,它的写法是这样的(公式来源: Wiki):

其中:
f ( q i , D ) f(q_i, D) f(qi,D) 是 q i q_i qi在文档D中的Term Frequency 1
I D F ( q i ) IDF(q_i) IDF(qi)是 q i q_i qi的Inverse Document Frequency 2
∣ D ∣ |D| ∣D∣为文章D的总词数
avgdl指average document length, 是你手头上所有文档长度的平均值
k 1 k_1 k1, b b b为自由参数,常见取值: k 1 ∈ [ 1.2 , 2.0 ] k_1\in[1.2,2.0] k1∈[1.2,2.0] , b = 0.75 b=0.75 b=0.75
下面我们来分析一下这个式子,解析这个式子的结构,看看里面的参数 k 1 k_1 k1, b b b到底有什么用。
首先,我们忽略 ∑ i = 1 n \sum_{i=1}^{n} ∑i=1n这个部分,即我们只看有关单个单词 q i q_i qi的计算。
接下来,我们拆出一个叫做 “ I D F IDF IDF板块” 的部分,即 I D F ( q i ) IDF(q_i) IDF(qi)。
然后,把剩下的视为一个叫 " T F TF TF板块"的部分。
于是我们有
S c o r e ( D , Q ) = ∑ 对 所 有 词 I D F 板 块 ⋅ T F 板 块 Score(D, Q) = \sum_{对所有词} IDF板块 \cdot TF板块 Score(D,Q)=对所有词∑IDF板块⋅TF板块
k 1 k_1 k1 的作用
这里最复杂的板块其实就是 T F TF TF板块了。那么我们先来想一个问题,如果我们简化 T F TF TF板块,它只等于 f ( q i , D ) f(q_i, D) f(qi,D) ,那么会发生什么?
那么,我们的BM25 Score将随着 q i q_i qi在文档D中出现的次数增加而增加,而且毫无上限。但也许我们不希望某个出现非常多的词带来的影响过大3,我们就来看看BM25里的 T F TF TF板块是如何防止这个影响过大的。
现在的 T F TF TF板块看起来有点复杂,我们来简化它。
首先,分母中的 ( 1 − b + b ⋅ ∣ D ∣ a v g d l ) (1-b+b\cdot\frac{|D|}{avgdl}) (1−b+b⋅avgdl∣D∣)只和b这个参数有关,当我们设置完b之后它就会变成一个常数,那么我们把这部分看成一个整体,设 m = ( 1 − b + b ⋅ ∣ D ∣ a v g d l ) m=(1-b+b\cdot\frac{|D|}{avgdl}) m=(1−b+b⋅avgdl∣D∣)。
另外 f ( q i , D ) f(q_i, D) f(qi,D)这个表达显得有点复杂,我们用小写 t f tf tf来表示它。
于是有
T F 板 块 = t f ⋅ ( k 1 + 1 ) t f + k 1 ⋅ m TF板块 = \frac{tf\cdot(k_1+1)}{tf+k_1\cdot m} TF板块=tf+k1⋅mtf⋅(k1+1)
再次简化:
T F 板 块 = k 1 + 1 1 + k 1 ⋅ m t f TF板块 = \frac{k_1+1}{1+\frac{k_1\cdot m}{tf}} TF板块=1+tfk1⋅mk1+1
发现了吗,这个式子是有上限的,不管tf再怎么大,这里的 T F TF TF板块也大不过 k 1 + 1 k_1+1 k1+1啊。
它的图像类似这样(以 k 1 = 1.2 k_1=1.2 k1=1.2, m = 1 m=1 m=1 为例):
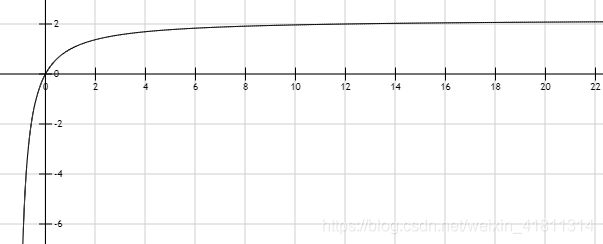
它的趋势不是一个窜天猴,而是渐近线。
所以说,BM25的 T F TF TF板块可以限制出现非常多次的单词对score的影响。
b b b 的作用
接下来,抛开我们已经理解的 T F TF TF大板块,只看其分母里的 m m m部分,以研究 b b b 这个参数的影响。
我们来重写一下m:
m = ( 1 − b + b ⋅ ∣ D ∣ a v g d l ) = 1 + b ⋅ ( ∣ D ∣ a v g d l − 1 ) m=(1-b+b\cdot\frac{|D|}{avgdl})\\ =1+b\cdot(\frac{|D|}{avgdl}-1) m=(1−b+b⋅avgdl∣D∣)=1+b⋅(avgdl∣D∣−1)
这里的 ∣ D ∣ a v g d l \frac{|D|}{avgdl} avgdl∣D∣看起来也太啰嗦了,它本质上就是当前文档相对于所有文档来说有多长,我们设它为 L L L, 总之,和当前文档长度有关。
于是有
m = 1 + b ⋅ ( L − 1 ) m=1+b\cdot(L-1) m=1+b⋅(L−1)
也就是说,( a v g d l avgdl avgdl不变的情况下) 当前文档越长, m m m越大,从而 T F TF TF板块值越小。
这样设计的原因,引用一个例子来解释: “如果在一个超长文章里我的名字被提到了一次,这篇文章是关于我的可能性估计不太大;但如果在一篇很短的文章里我的名字被提到了一次,那这篇文章是关于我的可能性还大些”。
那么参数 b b b 有什么用呢, b b b 越大,则对于长文的惩罚力度更大了。
终极总结
回到我们整体的三个板块
S c o r e ( D , Q ) = ∑ 对 所 有 词 I D F 板 块 ⋅ T F 板 块 Score(D, Q) = \sum_{对所有词} IDF板块 \cdot TF板块 Score(D,Q)=对所有词∑IDF板块⋅TF板块
进行一下终极总结:
- IDF板块帮助惩罚在所有文档中都高频出现的词的影响力
- TF板块帮助惩罚当前文档中高频出现的词的影响力,使得词影响力非随词频线性增长,而是渐近增长。最终TF板块的值不会大过 k 1 + 1 k_1+1 k1+1。
- TF板块帮助惩罚长文, b b b越大,惩罚力度越大。
转载请注明出处。
参考文档
- Wikipedia: Okapi BM25
- Elasticsearch: Practical BM25 - Part 2: The BM25 Algorithm and its Variables
Term Frequency一般指词 q i q_i qi在文章D中出现的个数 除以 文章D的总词数,旨在排除文章长度对TF的影响。不过,在BM25这个式子中的TF应该单纯是指词 q i q_i qi在文章D中出现的个数,参考elasticsearch对BM25的一个解释: “…which had the text “shane shane,” it would have f(“shane”,D) of 2.” ↩︎
IDF通常这样计算:
I D F ( q i ) = l n ( N − n ( q i ) + 0.5 n ( q i ) + 0.5 + 1 ) IDF(q_i) = ln(\frac{N-n(q_i)+0.5}{n(q_i)+0.5} + 1) IDF(qi)=ln(n(qi)+0.5N−n(qi)+0.5+1)
其中 N N N是手头上document总数量, n ( q i ) n(q_i) n(qi)是包含 q i q_i qi这个单词的文章总数量。
主旨是包含这个单词的文章越多,IDF值就越低。比如一些类似"a","the"的停止词,虽然它们的TF值可以很高,但它们的IDF值很可能很低,说明它们在哪都很容易出现,可能并无法给我们提供很多信息。 ↩︎你可能会问,那IDF不就帮助我们防止这个情况了吗?不,它们还是有一些区别的。当某个词在所有文档中都经常出现,那么IDF会帮助削减这个词的影响力。但如果某个词仅在当前文档内经常出现,IDF并不会帮助削减这个词的影响力。 ↩︎