AcWing 算法基础课第三节基础算法3 双指针、位运算、离散化、区间合并

1、该系列为ACWing中算法基础课，已购买正版，课程作者为yxc
2、y总培训真的是业界良心，大家有时间可以报一下
3、为啥写在这儿，问就是oneNote的内存不够了QAQ

本节内容：双指针、位运算、离散化、区间合并

一、双指针算法

1.1 双指针的类型

• 双指针指向两个序列
  对于两个序列，维护某种次序，例如归并排序合并两个有序序列的操作运用的就是双指针算法。
  
• 双指针指向一个序列（大多数）
  对于一个序列，用两个指针维护一段区间。例如，快排在划分区间时，两个指针维护一个区间
  

1.2 双指针写法通用模板

for(i=0, j=0; i<n; i++)
{
	while(j<i && check(i,j)) j++;
	// 每道题目的具体逻辑
}
虽然看起来是两重循环，但是每一个指针在所有循环里面移动次数不超过N，双指针则不超过2N。

双指针算法最核心的性质：优化，将O(N^2)的复杂度优化为O(N)。

未优化
for(int i=0; i<n;i++)
	for (int j=0; j<n; j++)

• 举例一：输入一个字符串 abc edf ghk，再将每个单词分别输出出来。

#include 
#include 

using namespace std;

int main()
{
	char str[1000];
	gets(str);
	// gets因为不会限制读入字符数量，因此被禁用，应使用fgets(名字,大小,stdin)；
	int n = strlen(str);
	for(int i=0; i<n; i++)
	{
		// 希望j停留在单词的最后一个字母
		int j = i;
		while(j<n && str[j]!=' ') j++;
		
		//这道题的具体逻辑
		for(int k = i; k< j; k++) cout << str[k];
		cout << endl;

		i=j; // 跳过整个区间
	}
	
	return 0;
}

• 举例二：最长连续不重复子序列。给定一个长度为 n 的整数序列，请找出最长的不包含重复的数的连续区间，输出它的长度。

朴素做法 O(N^2)
for (int i = 0; i < n; i ++ )
    for (int j = 0; j < i; j ++ )
        if(check(j,i))
        {
            res= max(res, i-j+1);
        }

双指针做法：红色箭头i遍历，绿色箭头j放在字符串不重复的最远的地方。由于指针具有单调性（随着i向后移动，j一定向后移动），可以优化代码。

    for (int i = 0, j=0; i < n; i ++ )
        while (j<=i && check(j,i)) j++; //  有重复元素
    res = max(res, i-j+1);

判断是否有重复数字的方法：维护一个数组s[N]，i向右移就加数字s[a[i]]++，j向右移就减数字s[a[j]]--，动态统计区间有多少数。如果新加的有重复元素，那么这个重复元素一定是a[i]，因此check(j,i)可以简写为a[j] != a[i]。完整代码如下

#include 

using namespace std;

const int N = 100010;
int a[N];
int s[N];
int n;

int main()
{
    cin >> n;
    for (int i = 0; i < n; i ++ ) cin >> a[i];
    
    int res = 0;
    for (int i = 0, j=0; i < n; i ++ ) 
    // 不用写j<=i因为，当j>i时不满足s[a[i]]>1 ，区间里没有数，一定满足要求没有重复的数）;
    {
        s[a[i]]++;
        while (s[a[i]]>1) 
        // 当有重复的数字时,一直找到a[i]==a[j]
        {       
            s[a[j]] --; 
            j++;
        }
        res = max(res, i-j+1);
    }
    cout << res << endl;
    return 0;
}

• 做题思路：先写出暴力方法的模板，再看i,j之间是否有单调关系，再进行优化

二、位运算

本节介绍位运算的常用操作

2.1 求n的第k位数字

n的二级制表示中第k位是几(个位是第0位)。

• 位运算的基本思路：
  • 先把第k位数字移到最后一位n >> k
  • 看个位是几x & 1
• 得到公式：

  n>>k &1
  

• 代码：

  #include 
  #include 
  
  using namespace std;
  
  int main()
  {
      int n = 10;
      
      for (int k = 3; k >= 0 ; k -- ) cout << (n >> k &1);
      
      return 0;
  }
  

2.2 返回n的最后一位1

lowbit操作是树状数组的基本操作之一，作用是返回n的最后一位1。

• lowbit是如何实现的：一个整数的负数是原数的补码（补码是取反加一），即-x = ~x+1，x&-x = x & (~x+1)
• 图解：
  

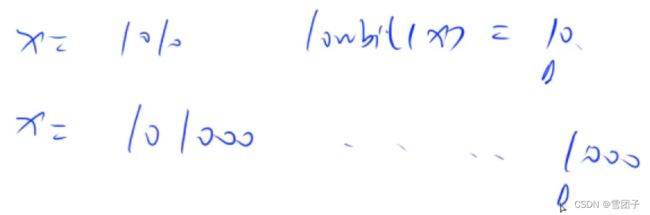
lowbit(n) = n & -n

• 应用：统计n里面1的个数

#include 

using namespace std;

// 给定一个长度为 n 的数列，请你求出数列中每个数的二进制表示中 1 的个数。
int lowbit(int x)
{
    return x & -x;
}

int main()
{
    int n;
    cin >> n;
    
    while (n -- )
    {
        int x;
        cin >> x;
        
        int res = 0;
        while(x) x -= lowbit(x), res ++; // 每次减去x的最后一位1
        
        cout << res << " ";
    }

    return 0;
}

2.3 原码反码补码相关知识

设x =1010

• 原码：0...01010
• 反码：1...10101
• 补码：1...10110
• 由于计算机的底层实现是没有减法的，而在数学上负数具有性质-x = 0-x。而0在做减法时需要借位由0...0变为10...00，因此用补码来表示负数。

三、离散化

这里特指整数的离散化。

3.1 离散化的基本含义

一组数，数的范围特别大（0-10^9），但个数少（10^5），有些题目我们需要将这些值作为下标，但是我们很难开一个10^9的数组。因此我们将这个序列映射到从0开始的连续的自然数。

• 例如：

• 这样的映射过程就被称为离散化（而且是保序的1）。

• 离散化中的问题：

  • 1、a[]数组中可能有重复元素，需要去重；
  • 2、如何算出a[i]离散化后的值是多少，或找到数x在a[]中的下标。（因为a是有序的，可以用二分法）；

3.2 离散化的步骤

• 第一步：排序去重，这些数字排好序的下标的就是映射后的值。常见写法如下（用vector进行离散化，java中用ArrayList）：

vector<int> alls; // 存储所有待离散化的值，假设alls是a[]数组
sort(alls.begin(), alls.end()); // 将所有值排序
alls.erase(unique(alls.begin(), alls.end()), alls.end()); // 去掉重复元素
// unique() 将所有重复元素去重，并返回去重后不重复位置末端点
// erase() 删掉重复的元素
例如：
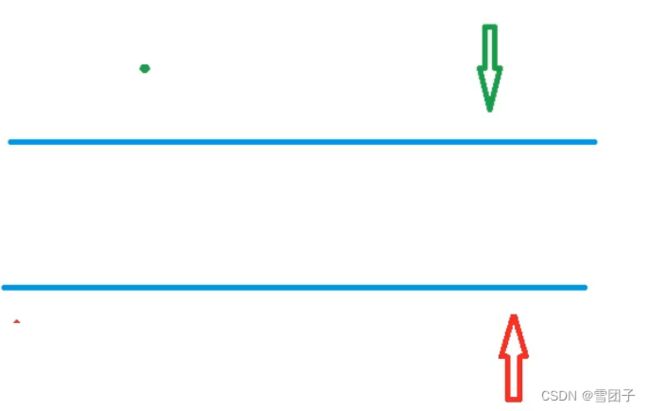
原数组：[1, 2, 100, 2000, 30000]
映射后：[0, 1, 2, 3, 4]

• 第二步：离散化，从0到数组n-1，找到x的位置

// 二分求出x对应的离散化的值
// 找到第一个大于等于x的位置
int find(int x)
{
    int l = 0, r = alls.size()-1;
    while(l<r)
    {
        int mid = l+r>>1;
        if (alls[mid]>=x) r = mid;
        else l = mid+1;
    }
    return r+1; // 映射到1,2,...,n，不加一从0,...n-1的映射
    // r是否加一与题目有关
}

• 举例：区间和
  • 假定有一个无限长的数轴，数轴上每个坐标上的数都是 0。现在，我们首先进行 n 次操作，每次操作将某一位置 x 上的数加 c。接下来，进行 m 次询问，每个询问包含两个整数 l 和 r，你需要求出在区间 [l,r] 之间的所有数的和。
    
  • 如果数据范围小（10^5），可以采用前缀和的方法，但本题是【10^-9 ——10^9】 且涉及到的数的个数很少（相加只用到n个x下标，查询只用到2m个下标，总共在2x10^9范围内只用到了3x10^5个数）。
  • 将所有用到的下标拿过来，映射到从1开始的自然数。如果x离散化之后是k，就让a[k]+=c，再求前缀和。

  #include 
  #include 
  #include 
  
  using namespace std;
  
  typedef pair<int, int> PII;
  
  const int N = 300010;
  
  int n,m;
  int a[N], s[N];
  
  vector<int> alls;
  vector<PII> adds, query;
  
  int find(int x) // 求x离散化后的结果
  {
      int l=0, r = alls.size()-1;
      while(l<r)
      {
          int mid = l+r >> 1;
          if(alls[mid]>=x) r = mid;
          else l = mid+1;
      }
      return r+1; // 从1开始
  }
  
  int main()
  {
      cin >> n >> m;
      for (int i = 0; i < n; i ++ )
      {
          int x, c;
          cin >> x >> c;
          
          adds.push_back({x,c}); // 加入要插入的位置和数字
          
          alls.push_back(x); // 下标加入离散化数组
      }
      
      for (int i = 0; i < m; i ++ )
      {
          int l, r; // 读左右区间
          cin >> l >> r;
          
          query.push_back({l, r});
          
          alls.push_back(l); // 区间加入离散化数组
          alls.push_back(r);
      }
      
      // 去重
      sort(alls.begin(), alls.end());
      alls.erase(unique(alls.begin(), alls.end()), alls.end());
      
      // 插入
      for(auto item:adds)
      {
          int x = find(item.first); // 找映射的值
          a[x] += item.second;      // 插入  
      }
      
      // 处理前缀和
      for (int i = 1; i <= alls.size(); i ++ ) s[i] = s[i-1]+a[i];
      
      // 询问区间和
      for (auto item:query)
      {
          int l = find(item.first);
          int r = find(item.second);
          cout << s[r] - s[l-1]  << endl;
      }
      return 0;
  }
  

补充，实现unique函数

unique函数实现原理：采用双指针，在有序数组的基础上选择不重复的第一个值。第一个指针是遍历到第几个数，第二个指针是存第几个数。

vector<int>::iterator unique(vector<int> &a)
{
	int j = 0;
	for(int i=0; i<a.size(); i++)
		if(!i || a[i]!=a[i-1])
			a[j++] = a[i]; 
			//满足这个性质就存到数组前面
			// a[0]——a[j-1]是所有不重复的数
	return a.begin()+j;
}
// 去重
sort(alls.begin(), alls.end());
alls.erase(unique(alls), alls.end());

四、区间和并

4.1 区间合并的含义

• 给n个区间，把所有有交集的区间进行合并，输出合并后的区间个数。
• 注意两个区间端点相交也会合并为同一个区间。
• 区间情况：1、区间A包含区间B；2、区间A与B相交；3、区间A与B不相交。（排过序之后，不可能有区间B包含区间A，即不存在B在A的左边）
• 样例：
  

4.1 区间合并的步骤

• 按照所有区间的左端点排序
• 扫描整个区间，扫描中维护一个当前的区间，将有交集的区间合并。
  -举例：给定 n 个区间 [l,r]，要求合并所有有交集的区间。注意如果在端点处相交，也算有交集。输出合并完成后的区间个数。例如：[1,3] 和 [2,6] 可以合并为一个区间 [1,6]。输出共一行，包含一个整数，表示合并区间完成后的区间个数。

#include 
#include 
#include 

using namespace std;

typedef pair<int, int> PII;

const int N = 100010;

int n;
vector<PII> segs;

// 区间合并
void merge(vector<PII> &segs)
{
    vector<PII> res; // 合并后的结果
    
    sort(segs.begin(), segs.end()); 
    // 优先以左端点排序，再以右端点排序；
     
    // 设置初始的负无穷到负无穷的边界值；
    // st代表区间开头，ed代表区间结尾，防止传空区间
    int st = -2e9, ed = -2e9;
    for (auto seg:segs)
    {
        if(ed < seg.first) 
        // 情况1：两个区间无法合并。当前区间在枚举区间的左边，没有交集，说明找到了一个完整的区间
        {
            if(st!=-2e9) res.push_back({st, ed});  // 防止初始值被记录，区间1放进res数组
            st = seg.first; // 维护区间2
            ed = seg.second;
        }
        else 
        // 情况2：两个区间可以合并，且区间1不包含区间2，区间2不包含区间1。有交集，更新右端点。
        // 或情况3：区间1包含区间2，此时不需要任何操作，可以省略。
        {
            ed = max(ed, seg.second); // 区间合并
        }
    }
    // 1、防止输入区间为空，即n=0，此时区间个数为1
    // 2、防止没有合并循环结束时的最后一个区间{st, ed}
    if (st != -2e9) res.push_back({st, ed});
    segs = res; // 区间更新为res
}

int main()
{
    cin >> n;
    
    for (int i = 0; i < n; i ++ )
    {
        int l, r;
        cin >> l >> r;
        segs.push_back({l,r});
    }
    
    merge(segs);
    
    cout << segs.size() << endl;
    
    return 0;
}