Spark MLlib ----- ALS算法

补充

在谈ALS（Alternating Least Squares）之前首先来谈谈LS，即最小二乘法。LS算法是ALS的基础，是一种数优化技术，也是一种常用的机器学习算法，他通过最小化误差平方和寻找数据的最佳匹配，利用最小二乘法寻找最优的未知数据，保证求的数据与已知的数据误差最小。LS也被用于拟合曲线，比如所熟悉的线性模型。
下面以简单的线性一元线性回归模型说明最小二乘法。假设我们有一组数据{(x1,y1),(x2,y2),(x3,y3)…}其符合线性回归，
假设其符合的函数为如下：
y = w₀ + w₁ x
我们使用一个平方差函数来表达参数的好坏，平方差函数如下：
L_n = (y_n - f(x;w₀,w₁))²
其中：
y: 目标变量或响应变量，是模型要预测的值。

x: 特征或自变量，是用来预测目标变量的输入。

w₁:斜率，表示每单位x变化时y的变化量。

w₀ :截距项，线性回归中表示直线与y轴的交点。

f(x;w₀,w₁): 线性回归模型的方程，表示预测y的函数，其中f 是模型，x 是输入特征w₁和w₀是模型的参数。
Ln:损失函数，用于衡量模型在给定数据点x_n,y_n处的预测值, f(x;w₀,w₁)与实际观测值 y_n之间的差异。
L越小表示参数w越精确，而这里最关键的就是寻找到最合适的w₀,w₁，则此时的数学表达式为：

将先行回归函数代入到最小二乘损失函数中，得到的结果为：

介绍完了LS，现在展开来说ALS算法。ALS算法本质上是基于物品的协同，近年来，基于模型的推荐算法ALS(交替最小二乘)在Netflix成功应用并取得显著效果提升，ALS使用机器学习算法建立用户和物品间的相互作用模型，进而去预测新项。

一、概念

ALS（Alternating Least Squares）是一种协同过滤推荐算法，主要用于处理推荐系统中的矩阵分解问题。它的基本思想是通过交替最小二乘法（Alternating Least Squares）来迭代地优化用户矩阵和物品矩阵。由于简单高效，已被广泛应用在推荐场景中，目前已经被集成到Spark MLlib和ML库中

二、算法概括

1. ALS算法用来补全用户评分矩阵。由于用户评分矩阵比较稀疏，将用户评分矩阵进行分解，变成V和U的乘积。通过求得V和U两个小的矩阵来补全用户评分矩阵。
2. ALS算法使用交替最小二乘法来进行求解。
3. ALS分为显示反馈和隐式反馈两种。显示反馈是指用户有明确的评分。对于商品推荐来说，大部分是通过用户的行为，获取隐式反馈的评分。隐式反馈评分矩阵需要进行处理，如果有用户评分则置为1，没有则赋值为0。但是对这个处理后的评分矩阵，再有一个置信度来评价这个评分。置信度等于1+a*用户真实评分
4. ALS的代价函数是估计值和现有的评分值误差的平方和，引入了L2正则。

2.1 协同过滤

协同过滤（Collaborative Filtering）是一种推荐系统的方法，通过分析用户的行为、偏好或兴趣，向用户推荐与其相似的其他用户喜欢的项目。其核心思想是基于用户之间的相似性或项目之间的相似性来进行推荐。

协同过滤分为两类：****基于用户的协同过滤和基于项目的协同过滤。

1. 基于用户的协同过滤（User-Based Collaborative Filtering）：

找出和目标用户兴趣相似的其他用户。如果两个用户在过去喜欢或不喜欢的项目上有相似的评价，那么在未来可能也会对相同或类似的项目有相似的兴趣。根据相似用户的行为给目标用户进行推荐。
2. 基于项目的协同过滤（Item-Based Collaborative Filtering）：
找出与目标项目相似的其他项目。如果用户喜欢某个项目，那么他们可能也会喜欢与该项目相似的其他项目。根据相似项目的特性给用户进行推荐。
协同过滤的优势在于不需要事先对用户或项目进行明确的描述，而是通过用户行为数据来自动学习用户的偏好。然而，它也面临一些挑战，如稀疏性、冷启动问题（新用户或新项目如何进行推荐）、计算复杂度等。

2.1.1 协同过滤实现

要实现协同过滤的推荐算法，要进行以下三个步骤：

1. 收集数据： 首先，需要获取用户对物品（如电影、图书、商品等）的评价数据。这些评价可以是用户的打分、购买历史、点击记录等。通常，这些数据是通过用户的交互行为收集的。
2. 找到相似用户和物品：

• 基于用户的协同过滤： 计算用户之间的相似性，通常使用一些相似性度量如余弦相似度或皮尔逊相关系数。找到与目标用户相似的其他用户，然后根据相似用户的行为给目标用户进行推荐。
• 基于物品的协同过滤： 计算物品之间的相似性，同样使用余弦相似度或其他度量。找到与目标物品相似的其他物品，然后将这些相似物品推荐给用户。
• 以下是几种计算相似度的方法：

  • 欧几里德距离:
    
    

  • 皮尔逊相关系数
    

  • Cosine 相似度
    

  • Tanimoto 系数
    

4. 进行推荐：

• 对于基于用户的协同过滤，可以根据相似用户的历史行为给目标用户推荐未看过的物品。
  • 基于用户的 CF 的基本思想相当简单，基于用户对物品的偏好找到相邻邻居用户，然后将邻居用户喜欢的推荐给当前用户。计算上，就是将一个用户对所有物品的偏好作为一个向量来计算用户之间的相似度，找到 K 邻居后，根据邻居的相似度权重以及他们对物品的偏好，预测当前用户没有偏好的未涉及物品，计算得到一个排序的物品列表作为推荐。 下图给出了一个例子，对于用户 A，根据用户的历史偏好，这里只计算得到一个邻居 - 用户 C，然后将用户 C 喜欢的物品 D 推荐给用户 A。
• 对于基于物品的协同过滤，可以将与用户喜欢的物品相似的其他物品推荐给用户。
  • 基于物品的 CF 的原理和基于用户的 CF 类似，只是在计算邻居时采用物品本身，而不是从用户的角度，即基于用户对物品的偏好找到相似的物品，然后根据用户的历史偏好，推荐相似的物品给他。从计算的角度看，就是将所有用户对某个物品的偏好作为一个向量来计算物品之间的相似度，得到物品的相似物品后，根据用户历史的偏好预测当前用户还没有表示偏好的物品，计算得到一个排序的物品列表作为推荐。下图给出了一个例子，对于物品 A，根据所有用户的历史偏好，喜欢物品 A 的用户都喜欢物品 C，得出物品 A 和物品 C 比较相似，而用户 C 喜欢物品 A，那么可以推断出用户 C 可能也喜欢物品 C。

注意：实际实现中，还需要考虑一些问题，如处理缺失数据、处理冷启动问题（新用户或新物品的推荐）、选择合适的相似性度量等。这些步骤通常在构建推荐系统时需要仔细考虑和调优。

2.1.2 计算复杂度

Item CF（基于物品的协同过滤）和User CF（基于用户的协同过滤）是协同过滤推荐系统中两个基本的策略。它们的性能和适用场景取决于系统的特点。

1. Item CF（基于物品的协同过滤）：

• 计算物品之间的相似度，然后根据用户过去喜欢的物品找到相似的物品进行推荐。
  适用于物品相对稳定，而用户数量较大的场景。
  不太受用户数量的影响，计算相似度的复杂度相对较低。

2. User CF（基于用户的协同过滤）：

• 计算用户之间的相似度，然后根据相似用户的历史行为给目标用户进行推荐。
  适用于用户相对稳定，而物品数量较大或更新频繁的场景。
  受用户数量影响较大，计算相似度的复杂度可能较高。

选择合适的算法取决于推荐系统所面对的具体情境和需求。在一些情况下，可以采用混合策略，结合两者的优势，以达到更好的推荐效果。例如，在实际应用中，可能会使用一种算法作为主推荐策略，另一种算法作为辅助推荐或冷启动时的备选策略。

User CF 是很早以前就提出来了，Item CF 是从 Amazon 的论文和专利发表之后（2001 年左右）开始流行，大家都觉得 Item CF 从性能和复杂度上比 User CF 更优，其中的一个主要原因就是对于一个在线网站，用户的数量往往大大超过物品的数量，同时物品的数据相对稳定，因此计算物品的相似度不但计算量较小，同时也不必频繁更新。但我们往往忽略了这种情况只适应于提供商品的电子商务网站，对于新闻，博客或者微内容的推荐系统，情况往往是相反的，物品的数量是海量的，同时也是更新频繁的，所以单从复杂度的角度，这两个算法在不同的系统中各有优势，推荐引擎的设计者需要根据自己应用的特点选择更加合适的算法。
所以这就引出来了，应用场景。对于不同的应用场景给出最优的计算方法。

2.1.3 应用场景

在非社交网络的网站中，内容内在的联系确实是推荐的重要原则之一，特别是在购物、阅读等场景下。以下是一些关键点：

1. Item CF 在内容相关性强的场景中的优势：

• 当用户在浏览某一内容（比如一本书）时，通过 Item CF 可以很自然地向用户推荐与当前内容相关的其他内容（相关书籍）。
• 这种推荐方式更加符合用户的当前兴趣和行为，有助于引导用户在网站上浏览更多相关内容。
• Item CF 的解释相对容易理解，因为推荐是基于物品之间的相似性，用户可以直观地理解为“因为你喜欢这个，所以我们为你推荐了类似的”。

2. User CF 在社交网络站点中的应用：

• 在社交网络站点中，用户之间的社交关系可以用于计算用户之间的相似性，因此 User CF 在这样的场景中更具优势。
• 结合社交网络信息，可以提高用户对推荐解释的信服程度。例如，推荐可以是“因为你的朋友喜欢这个，所以我们认为你可能也会喜欢”。

3. 混合策略的可能性：

• 有时候，可以采用混合策略，结合内容推荐和用户行为推荐，以提供更全面和个性化的推荐服务。
• 在不同场景下，可以动态选择合适的推荐算法，以满足用户的多样化需求。

推荐网站《推荐系统之算法综述》

2.2 ALS算法工作原理

1. ALS算法简介： ALS算法是一种协同过滤算法，最早于2008年提出，现已被集成到Spark的Mllib库中，使得在Spark平台上使用更加方便。

2. 协同过滤分类： ALS算法属于User-Item CF，即混合CF。它同时考虑了用户和物品两个方面。

3. 用户-物品关系： 用户和商品的关系可以表示为三元组（User, Item, Rating），其中Rating表示用户对商品的评分，反映用户对商品的喜好程度。

4. 矩阵规模： 在实际使用中，由于用户和物品的数量庞大，形成的Rating矩阵规模可能超过1亿项。传统矩阵分解方法难以处理如此大规模的数据。

5. 稀疏矩阵： 由于一个用户不太可能给所有商品评分，因此Rating矩阵是稀疏的，存在所谓的"missing item"，即缺失的评分项。

6. 建模方法： 为了更好地实现推荐系统，采用了矩阵分解（或矩阵补全）的方式。该方法寻找两个低维度的矩阵，使得它们的乘积近似等于原始的Rating矩阵，从而降低了数据的维度。

7. 矩阵分解目标： 假设用户和物品的数量分别为U和I，矩阵分解的目标是找到两个低维度的矩阵，它们的乘积近似等于原始的“用户-物品”矩阵。

总体来说，ALS算法通过降维技术处理大规模、稀疏的用户-物品评分矩阵，为推荐系统提供了一种有效的建模方法。

2.2.1 计算案例

	w	x	y	z
A			4.5	2.0
B		4.0		3.5
C			5.0
D			3.5	4.0

上述是给定的用户-物品矩阵中，找到低维度的因子矩阵是协同过滤算法的目标。这个问题通常通过矩阵分解的方法来解决。那么如何找到维度的因子矩阵呢？给出计算过程。

首先：我们希望将矩阵分解为两个较低维度的矩阵 U 和 V，使得 R≈U⋅V。
一般地，我们会初始化 U 和 V，然后通过交替最小二乘法迭代更新它们，使得 U⋅V 逼近 R。
具体步骤如下：

1. 初始化用户因子矩阵 U 和物品因子矩阵 V。这些因子通常是随机的小数。
2. 固定 U，通过最小化损失函数更新 V。最小化的目标是使预测评分 U⋅V 与实际评分 R 的差异最小化。这通常通过梯度下降等优化方法来完成。
3. 固定 U，通过最小化损失函数更新 V。最小化的目标是使预测评分 U⋅V 与实际评分 R 的差异最小化。这通常通过梯度下降等优化方法来完成。
4. 重复步骤2和3，直到达到收敛条件。

以下是一个简化的案例，演示如何使用ALS进行矩阵分解：
假设我们有一个用户-物品评分矩阵如下：

这里用户对电影的评分如图显示。使用pyspar进行案例演示。

from pyspark.ml.recommendation import ALS
from pyspark.sql import SparkSession

# 创建 Spark 会话
spark = SparkSession.builder.appName("ALSExample").getOrCreate()

# 创建示例数据
data = [(1, 1, 4), (1, 2, 5),
        (2, 1, 3), (2, 3, 2),
        (3, 2, 4), (3, 3, 5)]

# 创建DataFrame
df = spark.createDataFrame(data, ["userId", "movieId", "rating"])

# 使用ALS算法进行矩阵分解
als = ALS(rank=2, maxIter=5, regParam=0.01, userCol="userId", itemCol="movieId", ratingCol="rating")
model = als.fit(df)

# 获取用户因子矩阵U和物品因子矩阵V
user_factors = model.userFactors
item_factors = model.itemFactors

# 打印因子矩阵
print("User Factors:")
user_factors.show()

print("Item Factors:")
item_factors.show()

# 使用模型进行预测
predictions = model.transform(df)
predictions.show()

# 停止 Spark 会话
spark.stop()

ALS算法的核心思想，即通过找到两个低维度的因子矩阵来近似原始的用户-物品评分矩阵。以下是对文本的简要概括：

目标： ALS算法的目标是找到两个因子矩阵，一个用于表示用户（U×k维），另一个用于表示物品（k×I维），这两个矩阵的乘积近似等于原始的用户-物品评分矩阵。

因子矩阵： 因子矩阵是低维度的，通常为k维。这两个矩阵的乘积是原始评分矩阵的一个近似，通过这种方式实现对大规模、稀疏矩阵的降维处理。

稀疏矩阵与稠密矩阵： 原始评分矩阵通常是稀疏的，因为用户未对所有物品进行评分。而因子矩阵是稠密的，因为它们是完整的U×k和k×I矩阵，其中k是较低的维度。

满秩的因子矩阵： 因子矩阵是稠密的且满秩的，这意味着它们包含了原始矩阵的所有信息，通过这种方式可以在更低的维度上近似原始评分矩阵。

综上所述，ALS算法通过寻找适当的因子矩阵来实现对原始用户-物品评分矩阵的降维处理，从而在大规模稀疏数据中提供高效的推荐。

2.2.2 ALS算法输入的参数

我们的推荐系统是基于ALS算法中的train方法,我们之前的统计的一些指标都是为了这个推荐系统,把合适的商品推荐给需要的人群,提高用户体验和销售额,和京东淘宝的推荐也是类似的; ALS推荐基于隐语义模型, ALS算法共输入4个参数

参数一: 训练集

用户对我们这件商品的评分,用户点击了这件商品,我们就给一个评分,然后点击了这个商品的下一步又是多少评分,订单又是多少分,还有访问步长也有加权分,访问时常也有加权分,到最后付款,一共1分.

每一步的评分其实就是一个权重.也可以理解为用户对商品合适程度,喜好程度.用户和商品就组成了一个矩阵,只要用户点击了商品,就对这个商品有个评分了,而有的却没有点击,它是空白的,我们要做的就是填充这些空白,在空白处根据之前的权重预测一个评分.然后推荐.

假如预测分和真是分不匹配,我们就优化参数,线上观察效果,再优化权重分,参数.

训练集是用户，物品，评分.,是一个double类型

参数二: 特征值

给一个特征值,也是double类型的,可以很多参数,可以很少,这个是模型了,看你的模型设计了,如0.1,然后矩阵与特征相乘,所有的特征值与矩阵相乘的分相加,就得到了一个预测分.

假如预测分与实际分不同的话, 那就是特征值给的有问题了,可以修改特征值参数,直到和预测分类似即可.这就是那些算法工程师一直线上看效果,然后调参数了

参数三: 迭代参数

这个参数是让模型趋近于平稳,也是一个double值,也就是它的标准差越来越平稳,迭代之后会产生一个预测分,((预测分-真实分)的平方+预测分) / n 在发个方,这就是标准差,只要标准差越来越平稳,也就是收敛,就这OK了,.迭代参数就好了

参数四: 防过拟合参数

这个参数也是一个和double值,过拟合比如给机器看一个红色的苹果,突然给一张青色的苹果让它识别, 它就不认识这是一个苹果了,就是为了满足尽可能复杂的任务,我们给它的一个参数. 不妨参数的话,他就像一个单调函数,无法涵盖所有的点,而我们的目的就是为了涵盖大多数的点,如下图所示

三、具体代码

object AlsTest {

  val actToNum = udf{
    (str:String)=>{
      str match{
        case "BROWSE"=>1
        case "COLLECT"=>2
        case "BUYCAR"=>4
        case _ =>8
      }
    }
  }

  case class UserAction(act:String,act_time:String,cust_id:String,good_id:String,browse:String)
  def main(args: Array[String]): Unit = {
      val spark = SparkSession.builder().master("local[*]").appName("alstest").getOrCreate()
      val txt = spark.sparkContext.textFile("file:///D:/1016log/*.log").cache()
    //将读入的数据转为dataframe
    import spark.implicits._
    //计算出每个用户对该用户接触过的商品的评分
   var df =  txt.map(line=>{
      val arr = line.split(" ")
      UserAction(arr(0),arr(1),arr(2),arr(3),arr(4))
    }).toDF.select($"cust_id",$"good_id",actToNum($"act").as("score"))
        .groupBy("cust_id","good_id").agg(sum($"score").alias("score"))
     .cache()
    //为了防止用户编号或商品编号中含有给数字情况，所以要对所有的商品和用户编号给一个连续的对应的数字编号后在存到换存
    val wnd1 = Window.orderBy(desc("good_id"))
    val wnd2 = Window.orderBy(desc("cust_id"))

    val mm = new MySqlHandler
    
    val goodstab= mm.readMysql(spark,"goods")
      .select($"good_id",row_number().over(wnd1).alias("gid")).cache()

    val custtab = mm.readMysql(spark,"customs")
        .select($"cust_id",row_number().over(wnd2).alias("uid")).cache()
    //将df和goodstab和custtab join一下只保留元祖(gid uid score)

val df1 = df.join(goodstab, Seq("good_id"), "inner")
      .join(custtab, Seq("cust_id"), "inner")
      .select("gid", "uid", "score")

    //将稀疏表转为Rating对象集合
    val alldata = df1.rdd.map(row=>{
      Rating(row.getAs("uid").toString.toInt,row.getAs("gid").toString.toInt,row.getAs("score").toString.toFloat)
    })
    //将获得的Rating集合拆分为按照0.2.0.8两个集合
    val Array(train,test) = alldata.randomSplit(Array(0.8,0.2))
    //使用8成的数据去训练模型
    val model = new ALS().setRank(10).setIterations(20).setLambda(0.01).setImplicitPrefs(implicitPrefs = false).run(alldata)

//    val model = ALS.train(train, rank = 10, maxIter = 20, implicitPrefs = false)
    //对模型进行测试
    val tj = model.recommendProductsForUsers(30)
    tj.flatMap{
      case(user:Int,ratings:Array[Rating])=>
        ratings.map{
          case (rat:Rating)=>(user,rat.product,rat.rating)
        }
    }.foreach(println)
    spark.stop()
  }
}

四、具体案例----基于spark的电影推荐系统

4.1 使用spark ALS算法
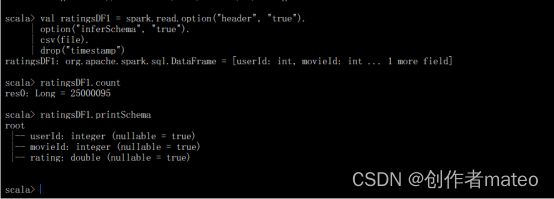
导入要用到的机器学习库：

加载数据集：

输出结果：

该数据集共有3个字段，分别是用户id、电影id和该用户对该电影的评分。
对数据进行简单统计：
看看被评分的电影总共有多少部：ratingsDF1.select(“movieId”).distinct().count

看看有多少用户参与评分：ratingsDF1.select(“userId”).distinct().count

快速检查谁是活跃的电影评分者：

分析每部电影的最大评分数量：

数据拆分，将原始数据集拆分为训练集和测试集，其中训练集占80%，测试集占20%：

使用Spark建立ALS算法(Alternating Least Square)。

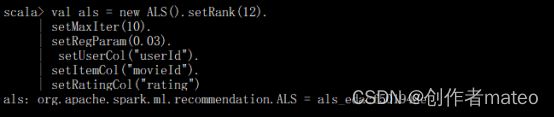
训练模型，并设置模型的冷启动策略
执行预测，并查看预测结果：

rating列为标签列，prediction为预测结果列。
有的预测值为NaN(非数字)，这会影响到rmse的计算，因些需要先删除结果集中的NaN值。

由以上输出内容可以看出，删除prediction列具有NaN值的记录以后，结果集中还有4996702条记录。
设置一个评估器（evaluator）来计算RMSE度量指标。

由以上输出内容可以看出，根均方差(rmse)值为0.7892022421096677。
使用ALSModel来执行推荐。
为所有用户推荐排名前五的电影：

为每部电影推荐top 3个用户：

由以上输出内容可以看出，为每部电影推荐前3个用户。
读取电影数据集，加上电影标题：
val moviesFile = “hdfs://master:9000/data/dataset/mlmovies.csv”
val moviesDF = spark.read.option(“header”, “true”).option(“inferSchema”, “true”).csv(moviesFile)
val recMoviesWithInfoDF = recMovies.join(moviesDF, “movieId”)
recMoviesWithInfoDF.select(“movieId”, “title”, “recommendations”).show(5, false)

使用CrossValidator对ALS模型进行调优。

使用找到的最优模型来再次进行预测，并对预测结果进行评估。