刷题 ------ 深度(DFS)与广度(BFS)优先搜索
文章目录
- 1.N叉树的最大深度
-
- (1)DFS
- (2)BFS
- 2.N叉树的前序遍历
-
- (1)DFS
- (2)迭代
- 3. N叉树的后序遍历
-
- (1)DFS
- 4.图像渲染
-
- (1) DFS
- (2) BFS
- 5.翻转二叉树
-
- (1)DFS
- (2)BFS
- 6.判断回文二叉树
-
- (1)DFS
- (2)BFS
- 7.寻找二叉搜索树中的目标节点
-
- (1)DFS
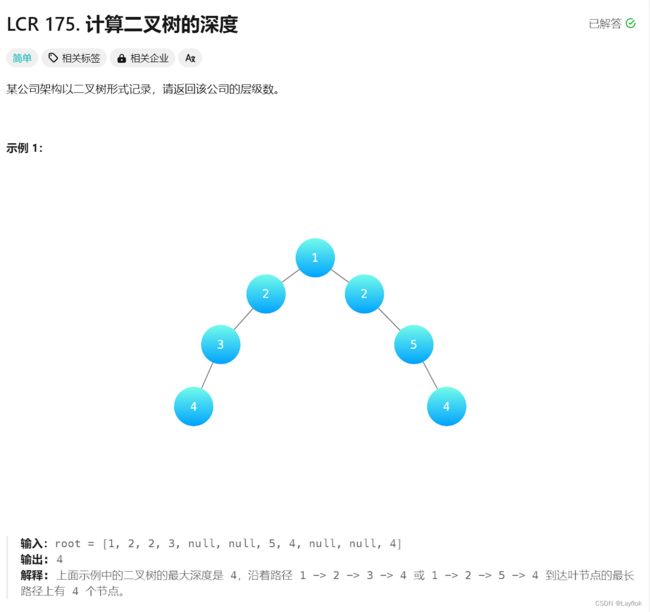
- 8.计算二叉树的深度
-
- (1)DFS
- (2)BFS
- 9.二叉树的最近公共先祖
-
- (1)DFS
- 10.彩灯装饰记录
-
- (1)BFS
- 11.寻找图中是否存在路径
-
- (1)DFS
- (2)BFS
- 12.传递信息
-
- (1)DFS
其实在上一边博客中 ----- 二叉树刷题,就能感觉到,对二叉树的遍历操作:
前中后序遍历是DFS
层序遍历则是BFS
1.N叉树的最大深度
如果对于这个 N 叉树里面的结构不是很理解,以前的博客中有B树,这个N叉树就是就是B树,只不过是是它没有分裂。

(1)DFS
这道题使用DFS来做的话,最主要的还是用到递归吧,和二叉树的深度感觉差不多。
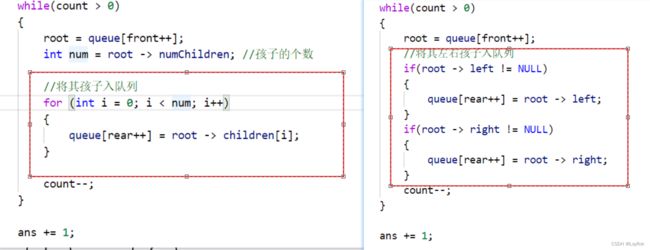
- 对于二叉树来说是遍历它的左右孩子,而对于这个N叉树来说肯定是去遍历它的所有孩子。
- 以前二叉树时候,只需要分别对于两个孩子写两句即可,而现在则是需要对其的所有孩子进行一个循环遍历。
int Max(int x, int y)
{
return x > y ? x : y;
}
int maxDepth(struct Node* root)
{
if(root == NULL)
{
return 0;
}
int num = root -> numChildren;
int max = 0; //最大的深度
//有孩子的话去依次遍历它的孩子
for (int i = 0; i < num; i++)
{
max = Max(max,maxDepth(root -> children[i]));
}
return max + 1;
}
(2)BFS
int maxDepth(struct TreeNode* root)
{
if(root == NULL)
{
return 0;
}
struct TreeNode** queue = (struct TreeNode**)malloc(sizeof(struct TreeNode*) * 10000);
int rear = 0, front = 0;
int ans = 0;
//根节点入队列
queue[rear++] = root;
//队列不为空
while(front != rear)
{
int count = rear - front;
while(count > 0)
{
root = queue[front++];
//将其左右孩子入队列
if(root -> left != NULL)
{
queue[rear++] = root -> left;
}
if(root -> right != NULL)
{
queue[rear++] = root -> right;
}
count--;
}
ans += 1;
}
return ans;
}
2.N叉树的前序遍历
(1)DFS
- 前序遍历,先将根节点存储下来,然后其数组正好也是从左到右的顺序
- 直接对其数组进行递归即可。
void DFS(struct Node* root,int* ans, int* size)
{
if(root == NULL)
{
return;
}
int num = root -> numChildren;
ans[(*size)++] = root -> val;
for (int i = 0; i < num; i++)
{
DFS(root -> children[i],ans,size);
}
}
int* preorder(struct Node* root, int* returnSize)
{
int* ans = (int*)malloc(sizeof(int) * 10000);
*returnSize = 0;
DFS(root,ans,returnSize);
return ans;
}
(2)迭代
- 运用下面这个算法,需要用到栈来辅助,
- 而我们将其孩子入栈的时候,将其倒着往前入栈。
int* preorder(struct Node* root, int* returnSize)
{
if(root == NULL)
{
*returnSize = 0;
return NULL;
}
struct Node** stack = (struct Node**)malloc(sizeof(struct Node*) * 10001);
int top = 0;
int* ans = (int*)malloc(sizeof(int) * 10000);
*returnSize = 0;
stack[++top] = root;
while(top != 0)
{
root = stack[top--];
ans[(*returnSize)++] = root -> val;
//将其孩子从后往前倒着入栈,出栈的时候就正好恢复了。
for (int i = root -> numChildren - 1; i >= 0; i--)
{
stack[++top] = root -> children[i];
}
}
return ans;
}
3. N叉树的后序遍历
(1)DFS
这和上一题中的前序遍历是一样的,就换一句话的位置就好了
- 当前根节点没有孩子(叶子节点) 或者是 当前根节点的孩子都循环完了,该录入自己了
void DFS(struct Node* root,int*ans,int* size)
{
if(root == NULL)
{
return;
}
int num = root -> numChildren;
for (int i = 0; i < num; i++)
{
DFS(root -> children[i],ans,size);
}
//当前根节点没有孩子(叶子节点) 或者是 当前根节点的孩子都循环完了,该录入自己了
ans[(*size)++] = root -> val;
}
int* postorder(struct Node* root, int* returnSize)
{
int* ans = (int*)malloc(sizeof(int) * 10000);
*returnSize = 0;
DFS(root,ans,returnSize);
return ans;
}
4.图像渲染

题目中的函数参数特别多,不要被吓到(手动狗头)。
题目中可以得出,只渲染颜色和自己相同的,但是前提是得能过去。也可以理解成油漆桶工具。
那么知道这样就好办了,我为了函数中没有太多的参数,所以定义了一些全局变量。
(1) DFS
-
row — 行 col — 列 newColor ---- 新颜色 curColor — 当前的颜色
-
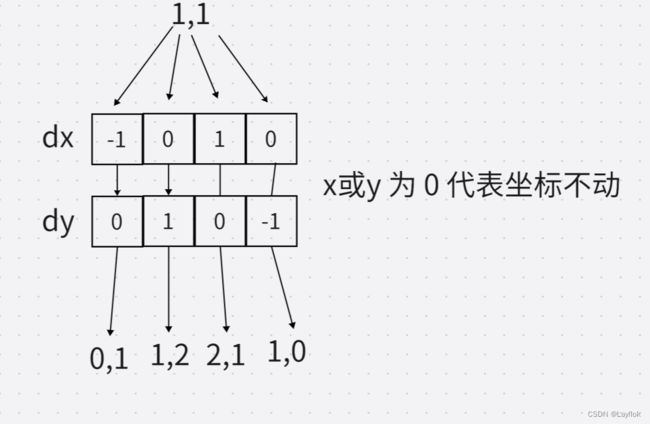
当进入DFS函数后,第一件事情就是去判断,当前坐标的颜色(数字)和原来的颜色数字是否一致,如果不一致的话就算了,
-
而DFS函数最核心的就是怎样去递归下去,我这边是顺时针的走。
int row,col; //原本图像的行和列
int newColor; //新颜色
int curColor; //现在的颜色
//检查所传的坐标是否合格
bool Check(int x,int y)
{
// x 和 y 都不能越界
return x >=0 && x < row && y >= 0 && y < col;
}
//x 和 y 是传过来的坐标
void DFS(int** image,int x, int y)
{
//不是现有的颜色不去渲染, 已经感染过的不去渲染
if(image[x][y] != curColor || image[x][y] == newColor)
{
return;
}
image[x][y] = newColor;
//代表上右下左四个坐标 顺时针
int coordX[4] = {-1,0,1,0};
int coordY[4] = {0,1,0,-1};
for (int i = 0; i < 4; i++)
{
int dx = x + coordX[i];
int dy = y + coordY[i];
//需要传的坐标符合条件
if(Check(dx,dy))
{
DFS(image,dx,dy);
}
}
}
int** floodFill(int** image, int imageSize, int* imageColSize, int sr, int sc, int color, int* returnSize, int** returnColumnSizes)
{
//初始化全局变量
row = imageSize;
col = *imageColSize;
newColor = color;
curColor = image[sr][sc];
//在原图形的进行修改,所以所有的行列都是原来的
*returnSize = imageSize;
*returnColumnSizes = imageColSize;
DFS(image,sr,sc);
return image;
}
(2) BFS
因为上面有许多全局变量,我下面也就没改,便于理解吧。
而BFS就需要用到一个队列了
- 首先将第一个坐标入队列,
- 然后判断队列中的坐标是否满足渲染的那个要求,如果满足的话,就将其值修改,然后将其的周围数字继续入队列,
- 否则啥也不干。
5.翻转二叉树
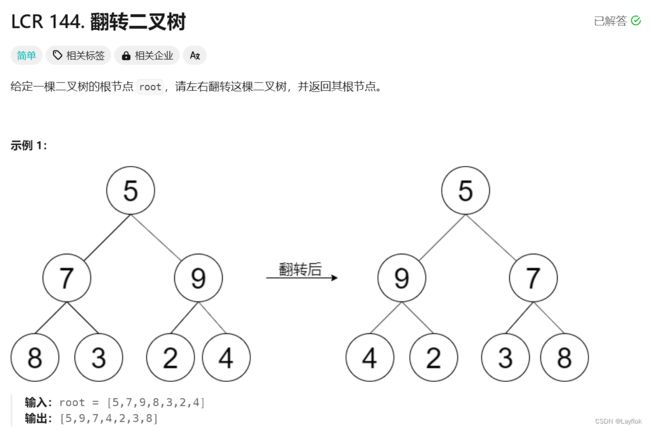
这道题在上一篇二叉树中也出现过,两道一模一样的题,上篇只是用DFS解决了,这次也用一下BFS。
(1)DFS
struct TreeNode* mirrorTree(struct TreeNode* root)
{
if(root == NULL)
{
return NULL;
}
struct TreeNode* leftChild = mirrorTree(root -> left);
struct TreeNode* rightChild = mirrorTree(root -> right);
root -> left = rightChild;
root -> right = leftChild;
return root;
}
(2)BFS
同样还是需要一个队列。
- 先将根节点入队列。
- 然后在出队列的时候,将左右孩子入队列,还得将左右孩子交换。
- 直到队列空为止。
struct TreeNode* mirrorTree(struct TreeNode* root)
{
if(root == NULL)
{
return NULL;
}
struct TreeNode** queue = (struct TreeNode**)malloc(sizeof(struct TreeNode*) * 10000);
int front = 0,rear = 0;
queue[rear++] = root;
while(front != rear)
{
//出队列
struct TreeNode* cur = queue[front++];
//将其左右孩子入队列
if(cur -> left != NULL)
{
queue[rear++] = cur -> left;
}
if(cur -> right != NULL)
{
queue[rear++] = cur -> right;
}
//交换左右孩子
struct TreeNode* tmp = cur -> left;
cur -> left = cur -> right;
cur -> right = tmp;
}
return root;
}
6.判断回文二叉树
(1)DFS
如果要用到DFS,我感觉就是你得先会,如何去判断两树是否是相同的。
然后利用根节点,它是一个二叉树嘛,所以将根节点的两个孩子单独拿出来,当成两个树,去判断这两个是否相同就好了。
//判断两树是否相同
bool IsEqual(struct TreeNode* r1,struct TreeNode* r2)
{
if(r1 == NULL && r2 == NULL)
{
return true;
}
if((r1 == NULL && r2 != NULL) ||(r1 != NULL && r2 == NULL))
{
return false;
}
if(r1 -> val != r2 -> val)
{
return false;
}
return IsEqual(r1 -> left, r2 -> right) && IsEqual(r1 -> right, r2 -> left);
}
bool checkSymmetricTree(struct TreeNode* root)
{
if(root == NULL)
{
return true;
}
return IsEqual(root -> left,root -> right);
}
(2)BFS
这个算法也就是普通的层序遍历,不一样的是,这次要把空指针也得入队列

看上面第一张图,如果不把空指针用-1表示,数组就会变成 3 3 那么它是回文的,但是实际上不是的。
- 先将根节点入队列。
- 在循环中,将每层的元素判断其是否回文。如果不回文直接返回false。
- 回文的话,将本层的所有节点同时出队列,在把他们的孩子节点入队列,如果孩子是空,入一个tmp,标记自己是 -1即可。
bool checkSymmetricTree(struct TreeNode* root)
{
if(root == NULL)
{
return true;
}
struct TreeNode** queue = (struct TreeNode**)malloc(sizeof(struct TreeNode*) * 1000);
int front = 0, rear = 0;
struct TreeNode* tmp = (struct TreeNode*)malloc(sizeof(struct TreeNode));
tmp -> val = -1;
tmp -> right = tmp -> left = NULL;
queue[rear++] = root;
while(front != rear)
{
int count = rear - front;
int i = front, j = rear - 1;
//判断数组是否回文
while(i < j)
{
if(queue[i] -> val != queue[j] -> val)
{
return false;
}
i++;
j--;
}
//出队列
while(count > 0)
{
root = queue[front++];
//代表不是空值
//入队列
if(root != tmp)
{
if(root -> left != NULL)
{
queue[rear++] = root -> left;
}
else
{
//是空指针就 赋为 tmp tmp val is -1 好比较
queue[rear++] = tmp;
}
if(root -> right != NULL)
{
queue[rear++] = root -> right;
}
else
{
queue[rear++] = tmp;
}
}
count--;
}
}
return true;
}
7.寻找二叉搜索树中的目标节点
(1)DFS
这就是二叉树的中序遍历把,遍历得到升序数组,然后取下标为size - cnt的值就是了。
void Inorder(struct TreeNode* root, int* nums,int* size)
{
if(root == NULL)
{
return;
}
Inorder(root -> left,nums,size);
nums[(*size)++] = root -> val;
Inorder(root -> right,nums,size);
}
int findTargetNode(struct TreeNode* root, int cnt)
{
int* nums = (int*)malloc(sizeof(int) * 10000);
int size = 0;
Inorder(root,nums,&size);
return nums[size - cnt];
}
8.计算二叉树的深度
二叉树的深度用DFS求了好多次了,这就不多阐述了。
好像没有用过BFS,BFS在上面的N叉树种求过深度。
(1)DFS
int calculateDepth(struct TreeNode* root)
{
if(root == NULL)
{
return 0;
}
//求左子树和右子树的深度
int leftdepth = calculateDepth(root -> left);
int rightdepth = calculateDepth(root -> right);
return (leftdepth > rightdepth ? leftdepth : rightdepth) + 1;
}
(2)BFS
- 将根节点入队列,然后在出队列的同时,将左右孩子入队列,
- 没进一次队列,就代表有一层深度
int calculateDepth(struct TreeNode* root)
{
if(root == NULL)
{
return 0;
}
struct TreeNode** queue = (struct TreeNode**)malloc(sizeof(struct TreeNode*) * 10001);
int front = 0,rear = 0;
int ans = 0;
queue[rear++] = root;
while(front < rear)
{
int count = rear - front;
//出队列
while(count > 0)
{
root = queue[front++];
//入队列
if(root -> left != NULL)
{
queue[rear++] = root -> left;
}
if(root -> right != NULL)
{
queue[rear++] = root -> right;
}
count--;
}
//进一次队列就有一层深度
ans += 1;
}
free(queue);
return ans;
}
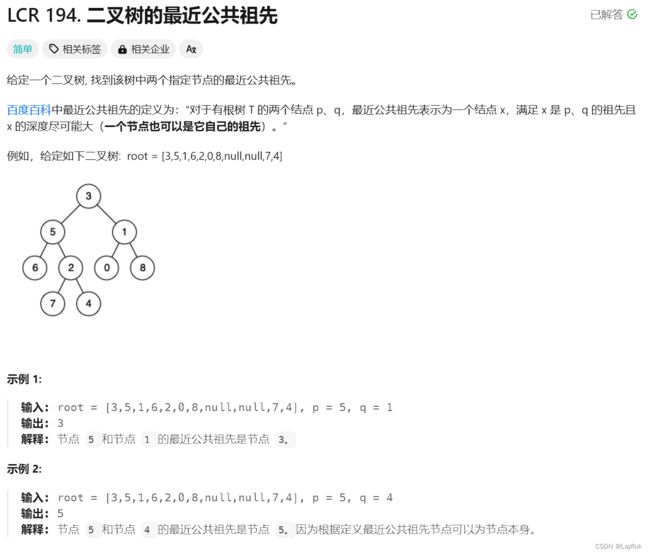
9.二叉树的最近公共先祖
(1)DFS
- 第一种情况:需要找的两个孩子在左右两侧。
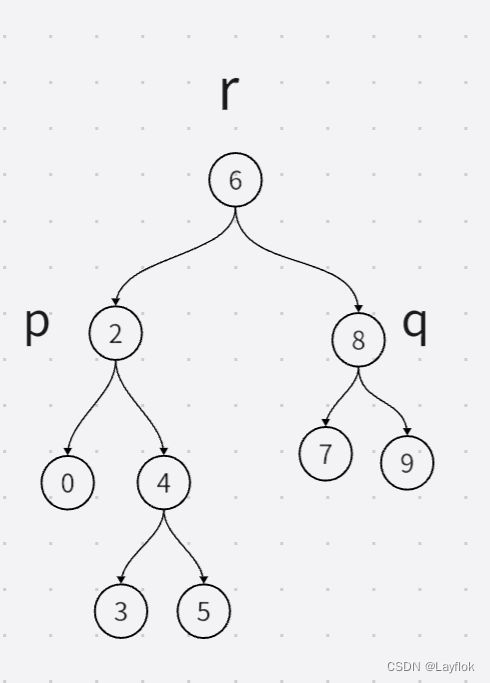
- 第二种情况,找的两个孩子中,其中有一个就是根节点

无非就以上两种情况而已,所以在递归函数中,分别用两left 和 right 去得到,
左右子树里,是否有所需找的节点,如果没有所需节点,那么就返回一个NULL。
如果左子树有,而右子树没有,就是上面所提到的第二中情况,直接返回那个不为空的就好了
如果不为空,意味着都找到了,返回当前的这个根节点就好了,就是第一种情况。
struct TreeNode* lowestCommonAncestor(struct TreeNode* root, struct TreeNode* p, struct TreeNode* q)
{
//找到了所对应的p 或者 q
if(root == p || root == q || root == NULL)
{
return root;
}
struct TreeNode* left = lowestCommonAncestor(root -> left,p,q);
struct TreeNode* right = lowestCommonAncestor(root -> right,p,q);
//左右孩子都不为空,证明找到了所对应的 p 和 q
if(left != NULL && right != NULL)
{
return root;
}
else if(left != NULL && right == NULL)
{
return left;
}
else if(left == NULL && right != NULL)
{
return right;
}
else
{
return NULL;
}
10.彩灯装饰记录
(1)BFS
这道题就是运用BFS算法对二叉树进行层序遍历,将其每层的数据放入一个二维数组中去,然后再用一个一个一维数组记录着每一层的大小。

层序遍历都会,这个两个数组之间关系一定得熟悉
#define MAX_SIZE 2000
int** decorateRecord(struct TreeNode* root, int* returnSize, int** returnColumnSizes)
{
if(root == NULL)
{
*returnSize = 0;
*returnColumnSizes = NULL;
return NULL;
}
//结果
int** ans = (int**)malloc(sizeof(int*) * MAX_SIZE);
*returnColumnSizes = (int*)malloc(sizeof(int) * MAX_SIZE);
int row = 0;
//队列
struct TreeNode** queue = (struct TreeNode**)malloc(sizeof(struct TreeNode*) * MAX_SIZE);
int front = 0, rear = 0;
queue[rear++] = root;
while(front != rear)
{
int count = rear - front; //当前层有多少个元素
//记录当前层的元素个数
(*returnColumnSizes)[row] = count;
//构造ans 大小为当前层的元素个数
ans[row] = (int*)malloc(sizeof(int) * count);
//临时变量,用于遍历数组
int index = 0,i = front,size = rear;
for (i = front; i < size; i++)
{
//出队列
root = queue[front++];
//将当前节点录入数组数组中去
ans[row][index++] = root->val;
//入队列
if (root->left != NULL)
{
queue[rear++] = root->left;
}
if (root->right != NULL)
{
queue[rear++] = root->right;
}
}
row++;
}
*returnSize = row;
return ans;
}
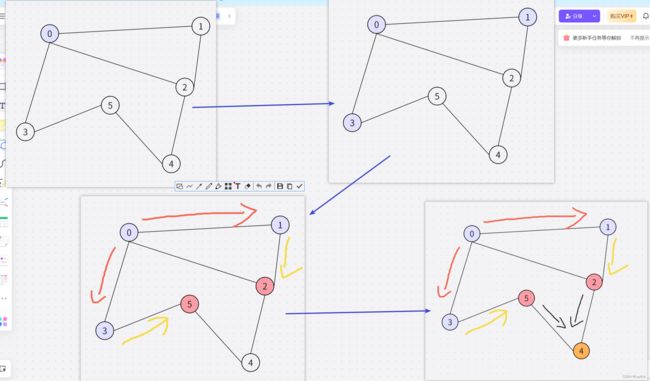
11.寻找图中是否存在路径

解答这道题能有三种方式:DFS BFS 并查集。其中并查集时间应该是最快的了,但本篇博客中,只讲DFS和BFS两种,循序渐进嘛。
而BFS和DFS又不能直接进行算法操作,在这道题中,必须借助图来实现。
并且图的存储方式必须是邻接表,用邻接矩阵会显示内存超出限制。
(1)DFS
- 首先呢,构造一张图出来,将所给的edges数组的中边录入到邻接表中去。
- 然后,去遍历整张图,和以往的在学图中的遍历有所不同。
- 以前再学习图中,再DFS算法的外层会嵌套一层for循环,如果图是非连通图会使得每一个节点都能访问。(如果对于图的概念不是很了解,以往的博客中有)
- 而现在的,咱们是需要对传过来的source进行图的遍历,如果访问不到dest的话,那么就证明过不去。
typedef struct Node
{
int adjvex;
struct Node* next;
}ArcNode; //边节点
typedef struct
{
int vex; //顶点
ArcNode* fristarc; //第一条边
}UList;
ArcNode* BuyNode(int adjvex)
{
ArcNode* newNode = (ArcNode*)malloc(sizeof(ArcNode));
newNode -> adjvex = adjvex;
newNode -> next = NULL;
return newNode;
}
void DFS(UList* G,int source,bool* visit)
{
//记录访问过了
visit[source] = true;
ArcNode* cur = G[source].fristarc;
//去遍历当前节点的所有边
while(cur != NULL)
{
//未访问过
if(visit[cur -> adjvex] != true)
{
DFS(G,cur -> adjvex,visit);
}
cur = cur -> next;
}
}
bool validPath(int n, int** edges, int edgesSize, int* edgesColSize, int source, int destination)
{
//无向图
UList* G = (UList*)malloc(sizeof(UList) * n);
int i;
//初始化图
for (i = 0 ; i < n; i++)
{
G[i].vex = n;
G[i].fristarc = NULL;
}
//录入边关系
for (i = 0; i < edgesSize; i++)
{
int x = edges[i][0];
int y = edges[i][1];
//无向图,对称的 x 先邻接 y
ArcNode* newNode1 = BuyNode(y);
newNode1 -> next = G[x].fristarc;
G[x].fristarc = newNode1;
//y 邻接 x
ArcNode* newNode2 = BuyNode(x);
newNode2 -> next = G[y].fristarc;
G[y].fristarc = newNode2;
}
bool* visit = (bool*)calloc(n,sizeof(bool));
DFS(G,source,visit);
return visit[destination] == true;
}
(2)BFS
相对于DFS那种一条路走到黑的,BFS算法则是往外扩张的。
- 先将所给的第一顶点入队列,(一旦入队列,就标记访问过)
- 然后在队列中进行出队列,出队列的同时,将其顶点有关的所有边全部都入队列。
下面代码中只有BFS算法的实现,其余的代码和DFS全部一样。
void BFS(UList* G,int source,bool* visit)
{
int* queue = (int*)malloc(sizeof(int) * size); //size 即 外部函数中的节点个数 n。
int front = 0, rear = 0;
queue[rear++] = source;
visit[source] = true;
while(front != rear)
{
int v = queue[front++];
ArcNode* cur = G[v].fristarc;
while(cur != NULL)
{
if(visit[cur -> adjvex] != true)
{
queue[rear++] = cur -> adjvex;
visit[cur -> adjvex] = true;
}
cur = cur -> next;
}
}
}
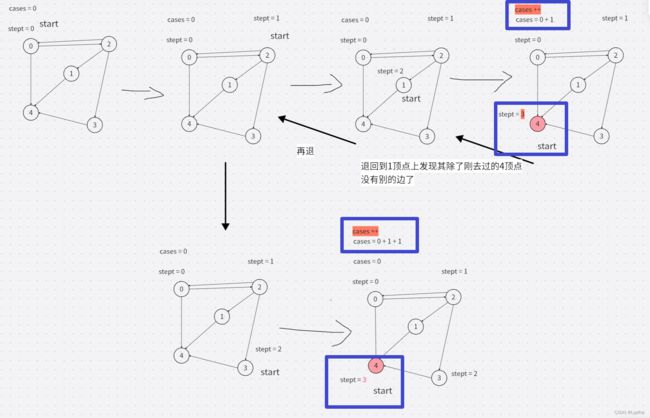
12.传递信息

下面和上一题运用了不同过的图的存储方式,下面是用的邻接矩阵的存储方式
(1)DFS
- 一直沿着一条边走,走到底,(底就是走到k)
- 然后去判断是否是 n -1 就好了
void DFS(int** matrix,int* cases,int start,int stept,int n, int k)
{
//步数未到
if(stept < k)
{
int i;
for (i = 0; i < n; i++)
{
//从 start 到 i 有边
if(matrix[start][i] != 0)
{
//可以走这一步
DFS(matrix,cases,i,stept+1,n,k);
}
}
}
else
{
//步数够 k 步, 结果也必须是对的
if(stept == k && start == n - 1)
{
(*cases)++;
}
}
}
int numWays(int n, int** relation, int relationSize, int* relationColSize, int k)
{
//邻接矩阵
int** matrix = (int**)malloc(sizeof(int*) * n);
int i,cases = 0;
for (i = 0; i < n; i++)
{
//初始化全为0
matrix[i] = (int*)calloc(n,sizeof(int));
}
//有向图的构造
for (i = 0; i < relationSize; i++)
{
int x = relation[i][0];
int y = relation[i][1];
matrix[x][y] = 1;
}
DFS(matrix,&cases,0,0,n,k);
return cases;
}