刷题 ------ 矩阵
文章目录
- 1.岛屿的周长
- 2.重塑矩阵
- 3.图片平滑器
- 4.托普利茨矩阵
- 5.翻转图像
- 6.转置矩阵
- 7. 可以被一步捕获的棋子数
- 8.距离顺序排列矩阵单元格
-
- 方法一 : BFS
- 方法二:排序
- 9.二维网格迁移
- 10.找出井字棋的获胜者
- 11.矩阵中战斗力最弱的k行
- 12.统计有序矩阵中的负数
-
- (1)暴力
- (2)二分
- 13.矩阵中的幸运数
- 14.矩阵对角元素的和
- 15.二进制矩阵中的特殊位置
-
- (1)暴力
- (2)模拟
- 16.最富有客户的资产总量
- 17.判断矩阵经轮转后是否一致
- 18.将一维数组转变成二维数组
-
- **优化**
- 19.检查是否每一行每一列都包含全部的整数
- 20.判断矩阵是否是一个X矩阵
- 21.矩阵中的局部最大值
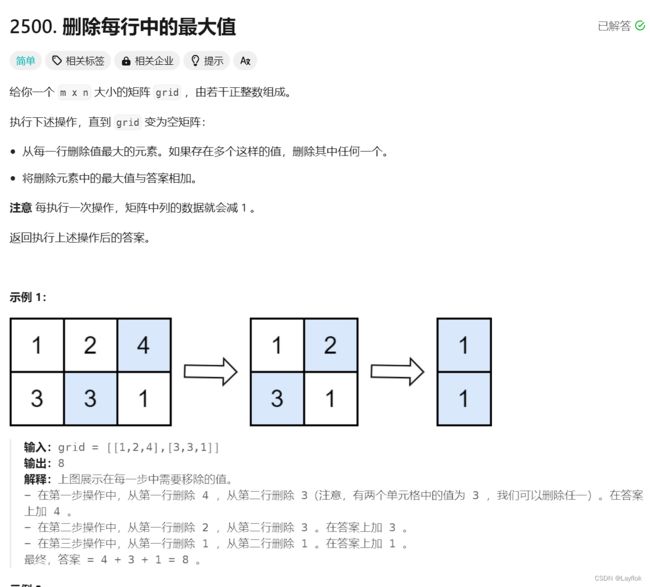
- 22.删除每行中的最大值
- 23.对角线上的质数
- 24.查询网格图中每一列的宽度
- 25.一最多的行
- 26.找到冠军
- 27.循环移位后的矩阵相似检查
- 28.找出缺失和重复的数字
- 29.无人机方阵
1.岛屿的周长

这道题其实就是上篇博客中所提到的DFS和BFS算法,但是在上一篇的间的题库中却没有,在矩阵里出现了。本人也是从开始,第一道题,慢慢的再刷,只是按照leetcode的题库去走的,有些题可能包含的不是很全。
- 因为题目中说岛屿是连在一起的,没有湖,所以我们只需要找到第一条上岸的边,然后运用DFS算法去遍历就好了。
- 但是要注意,因为它说的是周长,所以计入坐标中,啥也不干。
- 相反,如果需要越界的时候,或者是遇到水域的时候,它的边长才去增加。
- 同时标记着自己走过的路。
int row,col; //行和列
void DFS(int** grid,int x,int y,int* ans)
{
//遇到边界了
if(x < 0 || x >= row || y < 0 || y >= col)
{
(*ans) += 1;
return;
}
//水域就没有必要再递归遍历下去了
if(grid[x][y] == 0)
{
(*ans) += 1;
return;
}
if(grid[x][y] == 2)
{
//访问过了
return;
}
//标记访问过了
grid[x][y] = 2;
int coordX[4] = {1,0,-1,0};
int coordY[4] = {0,1,0,-1};
for (int i = 0; i < 4; i++)
{
int dx = x + coordX[i];
int dy = y + coordY[i];
DFS(grid,dx,dy,ans);
}
}
int islandPerimeter(int** grid, int gridSize, int* gridColSize)
{
int ans = 0;
row = gridSize;
col = *gridColSize;
int i,j;
for (i = 0; i < row; i++)
{
for (j = 0; j < col; j++)
{
if(grid[i][j] != 0)
{
break;
}
}
if(j != col)
{
break;
}
}
DFS(grid,i,j,&ans);
return ans;
}
2.重塑矩阵

可以直接想到的就是,将原来的矩阵进行遍历,然后得到一个行序遍历的数组,然后再将这个数组转化成其指定的 r * c 的矩阵
- 首先,遍历矩阵,得到一个行序遍历的数组
- 然后将行序遍历的数组,再转化为 r * c 的矩阵
这是最简单,最笨的方式
int** matrixReshape(int** mat, int matSize, int* matColSize, int r, int c, int* returnSize, int** returnColumnSizes)
{
int m = matSize;
int n = matColSize[0];
if (m * n != r * c)
{
*returnSize = matSize;
*returnColumnSizes = matColSize;
return mat;
}
//创建重塑的 r * c 的矩阵
int** ans = (int**)malloc(sizeof(int*) * r);
int i,j;
for (i = 0; i < r; i++)
{
ans[i] = (int*)malloc(sizeof(int) * c);
}
*returnSize = r;
*returnColumnSizes = (int*)malloc(sizeof(int) * r);
for (i = 0; i < r; i++)
{
(*returnColumnSizes)[i] = c;
}
//行序遍历数组
int* nums = (int*)malloc(sizeof(int) * (matSize * (*matColSize)) );
int numsSize = 0;
for (i = 0; i < matSize; i++)
{
for (j = 0; j < *matColSize; j++)
{
nums[numsSize++] = mat[i][j];
}
}
//将行序遍历数组转换会所给的 r * c 矩阵
numsSize = 0;
for (i = 0; i < r; i++)
{
for (j = 0; j < c; j++)
{
ans[i][j] = nums[numsSize++];
}
}
return ans;
}
还有一种方法就比较神奇了,也可叫一种对于矩阵转化的公式把个人感觉

int** matrixReshape(int** mat, int matSize, int* matColSize, int r, int c, int* returnSize, int** returnColumnSizes)
{
int row = matSize;
int col = *matColSize;
if(row * col != r * c)
{
*returnSize = matSize;
*returnColumnSizes = matColSize;
return mat;
}
//创建重塑矩阵
int i;
int** ans = (int**)malloc(sizeof(int*) * r);
*returnSize = r;
*returnColumnSizes = (int*)malloc(sizeof(int) * r);
for (i = 0; i < r; i++)
{
(*returnColumnSizes)[i] = c;
ans[i] = (int*)malloc(sizeof(int) * c);
}
for (i = 0; i < row * col; i++)
{
ans[i / c][i % c] = mat[i / col][i % col];
}
return ans;
}
3.图片平滑器
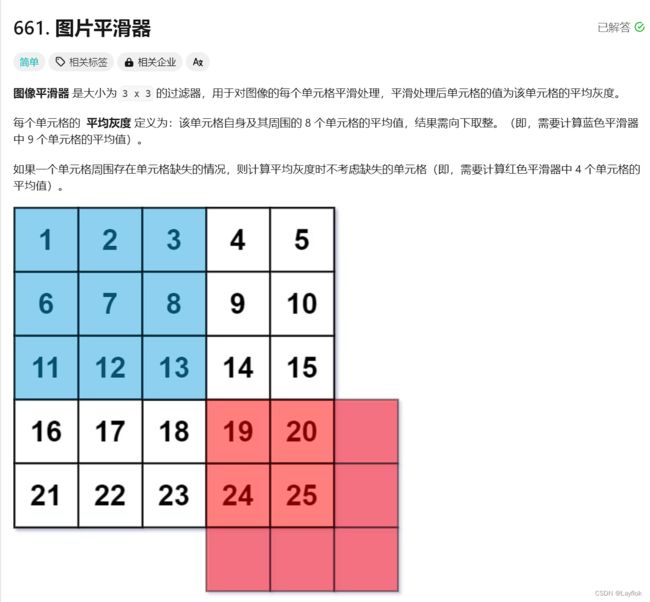
这道题就是计算出自身周围,9宫格嘛,内的平均值,然后将自身的值改掉。
最后开始做的时候,没看清楚题,我以为他是动态的,就是走一步,然后在矩阵中的全部9空格的数据全部改成平均值,所以在外面封装了一个函数,到最后发现只改一个,也就没改了,这道题完全可以在主函数中实现。
- 计算平均值都会,只要是判断好他的界限就好了。
int row,col;
//8个方位
int coordX[8] = {-1,-1,-1,0,1,1,1,0};
int coordY[8] = {-1,0,1,1,1,0,-1,-1};
int AverageGet(int** img,int x, int y)
{
int sum = img[x][y];
int count = 1;
for (int i = 0; i < 8; i++)
{
int dx = x + coordX[i];
int dy = y + coordY[i];
//合理的范围
if(dx >= 0 && dx < row && dy >= 0 && dy < col)
{
sum += img[dx][dy];
//printf("img[%d][%d] = %d sum = %d\n",dx,dy,img[dx][dy],sum);
count++;
}
}
// printf("%d\n",sum / count);
return sum / count;
}
int** imageSmoother(int** img, int imgSize, int* imgColSize, int* returnSize, int** returnColumnSizes)
{
int i,j;
row = imgSize;
col = imgColSize[0];
///初始化
int** ans = (int**)malloc(sizeof(int*) * row);
*returnSize = row;
*returnColumnSizes = (int*)malloc(sizeof(int) * row);
for (i = 0; i < row; i++)
{
ans[i] = (int*)malloc(sizeof(int) * col);
(*returnColumnSizes)[i] = col;
}
//遍历每一个元素
for (i = 0; i < row; i++)
{
for (j = 0; j < col; j++)
{
int ave = AverageGet(img,i,j);
ans[i][j] = ave;
}
}
return ans;
}
4.托普利茨矩阵
- 对这个矩阵(二维数组)进行遍历。
- 然后去判断当前的斜下方的数据是否与当前相同即可
- 但要注意遍历的范围,小心越界,行和列遍历到前一个就好了。
bool isToeplitzMatrix(int** matrix, int matrixSize, int* matrixColSize)
{
int i,j;
int row = matrixSize;
int col = matrixColSize[0];
for(i = 0; i < row - 1; i++)
{
for (j = 0; j < col - 1; j++)
{
//斜对角访问
if(matrix[i][j] != matrix[i+1][j+1])
{
return false;
}
}
}
return true;
}
5.翻转图像

题目中说水平就是逆序数组,反转就是将 0 改成1 将 1 改成 0
- 遍历矩阵的每一行,然后对没一行进行逆序和反转即可。
int Helper(int x)
{
return x == 1 ? 0 : 1;
}
int** flipAndInvertImage(int** image, int imageSize, int* imageColSize, int* returnSize, int** returnColumnSizes)
{
int row = imageSize;
int col = imageColSize[0];
//原地修改即可
*returnSize = row;
*returnColumnSizes = imageColSize;
int i,j;
for (i = 0; i < row; i++)
{
int left = 0,right = col - 1;
while(left <= right)
{
//将 0 和 1 进行转换
if(left == right)
{
//只剩一个元素时候
image[i][left] = Helper(image[i][left]);
break;
}
image[i][left] = Helper(image[i][left]);
image[i][right] = Helper(image[i][right]);
//交换
int tmp = image[i][left];
image[i][left++] = image[i][right];
image[i][right--] = tmp;
}
}
return image;
}
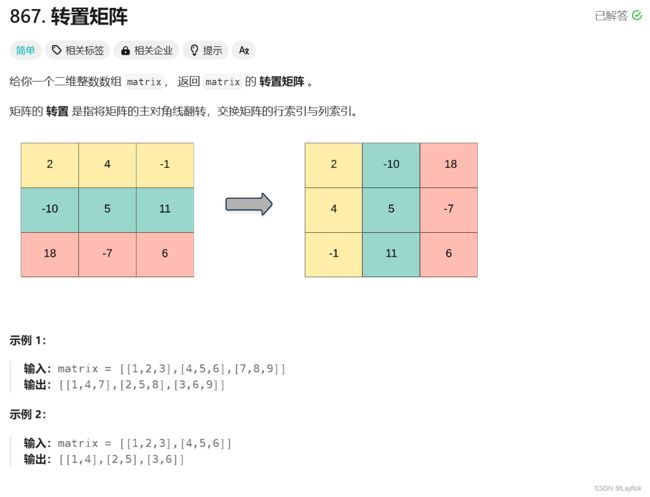
6.转置矩阵
- 将原来的行列互换。
int** transpose(int** matrix, int matrixSize, int* matrixColSize, int* returnSize, int** returnColumnSizes)
{
int row = matrixSize;
int col = matrixColSize[0];
int i;
int** ans = (int**)malloc(sizeof(int*) * col);
*returnSize = col;
*returnColumnSizes = (int*)malloc(sizeof(int) * col);
for (i = 0; i < col; i++)
{
(*returnColumnSizes)[i] = row;
ans[i] = (int*)malloc(sizeof(int) * row);
}
for (i = 0; i < row; i++)
{
for (int j = 0; j < col; j++)
{
ans[j][i] = matrix[i][j];
}
}
return ans;
}
7. 可以被一步捕获的棋子数
- 这道题,就是去遍历这个二维数组,首先得找到图中的车在哪里?
- 找到车之后,对车的位置,进行上下左右四个方位的遍历
- 一旦发现遇到卒或者象就停止循环,要注意的是遇到卒的时候count自增。
int numRookCaptures(char** board, int boardSize, int* boardColSize)
{
int count = 0;
int row = boardSize;
int col = boardColSize[0];
int i,j;
//找车Rook
for (i = 0; i < row; i++)
{
for (j = 0; j < col; j++)
{
if(board[i][j] == 'R')
{
break;
}
}
if(j != col)
{
break;
}
}
//至此,i和j就是车的位置
//printf("i = %d,j = %d\n",i,j);
int k;
//上
for (k = i - 1; k >= 0; k--)
{
//碰到象了
if(board[k][j] == 'B')
{
break;
}
//碰到卒
if(board[k][j] == 'p')
{
count++;
break;
}
}
//下
for (k = i + 1; k < row; k++)
{
//碰到象了
if(board[k][j] == 'B')
{
break;
}
//碰到卒
if(board[k][j] == 'p')
{
count++;
break;
}
}
//左
for (k = j - 1; k >= 0; k--)
{
//碰到象了
if(board[i][k] == 'B')
{
break;
}
//碰到卒
if(board[i][k] == 'p')
{
count++;
break;
}
}
//右
for (k = j + 1; k < col; k++)
{
//碰到象了
if(board[i][k] == 'B')
{
break;
}
//碰到卒
if(board[i][k] == 'p')
{
count++;
break;
}
}
return count;
}
8.距离顺序排列矩阵单元格

题目有点绕,难理解,多看几遍就好了,大致意思就是说。
给你一个 rows*cols 的矩阵然后再给你一个坐标(r,c)。然后把矩阵中的所有坐标从到当前这个坐标的位置,从小到大排列出来。
看懂题目,首先想到的就是BFS了吧
方法一 : BFS
- 构造一个队列和visit数组,这个visit数组用于标志是否访问过
- 然后就运用BFS入队列,最后返回这个队列就好了。
int** allCellsDistOrder(int rows, int cols, int rCenter, int cCenter, int* returnSize, int** returnColumnSizes)
{
int size = rows * cols;
int i;
int** queue = (int**)malloc(sizeof(int*) * size); //队列
int front = 0,rear = 0;
*returnSize = size;
*returnColumnSizes = (int*)malloc(sizeof(int) * size);
for (i = 0; i < size; i++)
{
(*returnColumnSizes)[i] = 2;
queue[i] = (int*)malloc(sizeof(int) * 2);
}
//标记访问过的
int** visit = (int**)malloc(sizeof(int*) * rows);
for (i = 0; i < rows; i++)
{
visit[i] = (int*)calloc(cols,sizeof(int));
}
//将所给的当前下标入队列
queue[rear][0] = rCenter;
queue[rear++][1] = cCenter;
visit[rCenter][cCenter] = 1;
//上右下左 顺时针
int coordX[4] = {-1,0,1,0};
int coordY[4] = {0,1,0,-1};
while(front < rear)
{
//出队列
int x = queue[front][0];
int y = queue[front++][1];
//广度优先入队列
for (int k = 0; k < 4; k++)
{
int dx = x + coordX[k];
int dy = y + coordY[k];
//未超出范围,
if(dx >= 0 && dx < rows && dy >= 0 && dy < cols)
{
//并且没有被访问过
if(visit[dx][dy] != 1)
{
queue[rear][0] = dx;
queue[rear++][1] = dy;
visit[dx][dy] = 1;
}
}
}
}
return queue;
}
方法二:排序
- 首先将所有坐标与当前所给的坐标放在一个二维数组中去
- 然后对二维数组进行一个排序。
int cmp_dis(const void* x,const void* y)
{
return ((int**)x)[0][2] - ((int**)y)[0][2];
}
int** allCellsDistOrder(int rows, int cols, int rCenter, int cCenter, int* returnSize, int** returnColumnSizes)
{
int i,j,index = 0;//index 是 ans 的索引
int size = rows * cols;
int** ans = (int**)malloc(sizeof(int*) * size);
*returnSize = size;
*returnColumnSizes = (int*)malloc(sizeof(int) * size); //将距离传进去
for (i = 0; i < size; i++)
{
(*returnColumnSizes)[i] = 2; //返回大小为2,不返回距离即可
ans[i] = (int*)malloc(sizeof(int) * 3); //多开辟一个空间,来存放距离
}
for (i = 0; i < rows; i++)
{
for (j = 0; j < cols; j++)
{
ans[index][0] = i;
ans[index][1] = j;
ans[index++][2] = abs(i - rCenter) + abs(j - cCenter);
}
}
//排序
qsort(ans,size,sizeof(ans[0]),cmp_dis);
return ans;
}
9.二维网格迁移

可以发现就是只有最后一列变换的时候的特殊的,其余的都是往后挪动一列,那么把这个最后一列单独搞出来就好了
- 将矩阵从后往前,将前一列的赋值给当前这一列。
- 然后将最后一列,独自摘出来。
- 从上图就能够发现,最后一列的最后一个数据9变成了开始的第一个数据了
int** shiftGrid(int** grid, int gridSize, int* gridColSize, int k, int* returnSize, int** returnColumnSizes)
{
int i;
int row = gridSize;
int col = gridColSize[0];
*returnSize = row;
*returnColumnSizes = gridColSize;
int count = k % (row * col);
for (i = 0; i < count; i++)
{
int* nums = (int*)malloc(sizeof(int) * row); //最后一列的数据
int index = 1;//注意是从一开始
int x,y;
//只有一列
if(col == 1)
{
for (x = 0; x < row; x++)
{
if(x != row -1)
nums[index++] = grid[x][0];
else
nums[0] = grid[x][0];
}
}
//不止一列
for (x = 0; x < row; x++)
{
for (y = col-1; y > 0; y--)
{
//最后一列的元素单独拿出来到nums中去
if(y == col - 1)
{
if(x == row -1)
nums[0] = grid[x][y];
else
nums[index++] = grid[x][y];
}
grid[x][y] = grid[x][y-1];
}
}
//将最后一列放入第一列中去
for (x = 0; x < row; x++)
{
printf("%d ",nums[x]);
grid[x][0] = nums[x];
}
}
return grid;
}
10.找出井字棋的获胜者
void CreateAns(char* s,int val)
{
if(val == 1)
{
s[0] = 'A';
s[1] = '\0';
}
else
{
s[0] = 'B';
s[1] = '\0';
}
}
char* tictactoe(int** moves, int movesSize, int* movesColSize)
{
char* ans = (char*)malloc(sizeof(char) * 8);
//少于5步,不可能有结果
if(movesSize < 5)
{
strcpy(ans,"Pending");
return ans;
}
int row = 3;
int col = 3;
int i,j;
//棋盘 0 代表空 1 代表A 2 代表 B
int** board = (int**)malloc(sizeof(int*) * row);
for (i = 0; i < row; i++)
{
board[i] = (int*)calloc(col,sizeof(int));
}
//构造棋盘样式
for (i = 0; i < movesSize; i++)
{
int x = moves[i][0];
int y = moves[i][1];
//偶数 A
if(i % 2 == 0)
{
board[x][y] = 1;
}
else
{
board[x][y] = 2;
}
}
//打印棋盘
for (i = 0; i < row; i++)
{
for (j = 0; j < col; j++)
{
printf("%d ",board[i][j]);
}
printf("\n");
}
//判断那一个玩家赢
//三行
for (i = 0; i < row; i++)
{
if(board[i][0] == board[i][1] && board[i][1] == board[i][2] && board[i][0] != 0)
{
CreateAns(ans,board[i][0]);
return ans;
}
}
//三列
for (i = 0; i < row; i++)
{
if(board[0][i] == board[1][i] && board[1][i] == board[2][i] && board[0][i] != 0)
{
CreateAns(ans,board[0][i]);
return ans;
}
}
//对角线
if(board[0][0] == board[1][1] && board[1][1] == board[2][2] && board[2][2] != 0)
{
CreateAns(ans,board[0][0]);
return ans;
}
//副对角线
if(board[0][2] == board[1][1] && board[1][1] == board[2][0] && board[2][0] != 0)
{
CreateAns(ans,board[0][2]);
return ans;
}
if(movesSize == 9)
{
strcpy(ans,"Draw");
return ans;
}
strcpy(ans,"Pending");
return ans;
}
11.矩阵中战斗力最弱的k行

在记录军人出现的次数时候,题目中说军人都出现在前面,所以如果在矩阵中出现0就直接可以停止循环,以后都不会出现军人了。(题解中是用二分法去查找最后一个1出现的位置)
- 将每一行的军人和每一行的下标记录到哈希表中去。
- 然后将其按照出现的次数排序,
- 这时候返回前k个索引就好了
typedef struct Hash
{
int index;
int count;
}Hash;
int cmp_count(const void* x, const void* y)
{
return ((Hash*)x) -> count - ((Hash*)y) -> count;
}
int* kWeakestRows(int** mat, int matSize, int* matColSize, int k, int* returnSize)
{
int row = matSize,col = matColSize[0];
Hash* map = (Hash*)malloc(sizeof(Hash) * matSize);
int* ans = (int*)malloc(sizeof(int) * k);
int index = 0;
int i,j;
for (i = 0; i < row; i++)
{
int count = 0;
for (j = 0; j < col; j++)
{
//0以后不会再有1了
if(mat[i][j] == 0)
{
break;
}
count++;
}
map[index].index = i;
map[index++].count = count;
}
//按照其军人出现次数进行排序
qsort(map,row,sizeof(map[0]),cmp_count);
//将前k个元素导入数组中去
index = 0;
for (i = 0; i < k; i++)
{
ans[index++] = map[i].index;
}
*returnSize = k;
return ans;
}
12.统计有序矩阵中的负数
直接暴力遍历整个矩阵统计其负数即可,但是题目中都说了是有序的,所以用二分法肯定也错了。
(1)暴力
因为他是有序的,所以从后往前可以节省大量的时间
int countNegatives(int** grid, int gridSize, int* gridColSize)
{
int row = gridSize;
int col = gridColSize[0];
int i,j,count = 0;
for (i = 0; i < row; i++)
{
for (j = col - 1; j >= 0; j--)
{
if(grid[i][j] >= 0)
{
break;
}
count++;
}
}
return count;
}
(2)二分
我靠了,哎呦喂,啥呀这是,left = -1 right = size;
不能是 0 和 size -1 做吗? 从 0 和size - 1做了老久,做不出来。各位有会的吗?欢迎评论啊。。
int countNegatives(int** grid, int gridSize, int* gridColSize)
{
int row = gridSize;
int col = gridColSize[0];
int i,count = 0;
for (i = 0; i < row; i++)
{
//有没有这样的 left = 0 right = col - 1; 搞半天出不来,
int left = -1,right = col;
while(left + 1 != right)
{
int mid = (left + right) / 2;
if(grid[i][mid] >= 0)
{
left = mid;
}
else
{
right = mid;
}
}
count += col - right;
}
return count;
}
13.矩阵中的幸运数
- 遍历矩阵的每一行,然后去找出那个最小值
- 然后在遍历当前最小值所在的这一列,
- 如果没有比当前值大的,那么整个值就是幸运数。
这道题我在刚做的时候是开辟了matrix 的大小,我以为幸运数最多每行一个,结果后续看题解,幸运数只有一个,有修改了修改,提高了点时间。
int* luckyNumbers (int** matrix, int matrixSize, int* matrixColSize, int* returnSize)
{
int row = matrixSize;
int col = matrixColSize[0];
int* ans = (int*)malloc(sizeof(int));
int i,j;
for (i = 0; i < row; i++)
{
int minNum = matrix[i][0];
int x = i,y = 0;
//去找当前行最小的那个数,已经其下标。
for (j = 1; j < col; j++)
{
if(matrix[i][j] < minNum)
{
y = j;
minNum = matrix[i][j];
}
}
//判断其是否也是当前列最大的数字
//向上
int flag = 0;
for (j = x - 1; j >= 0; j--)
{
//有一个比它大的就不行
if(matrix[j][y] > minNum)
{
flag = 1;
break;
}
}
//向下(如果上面发现了比他大的那么下面就不用去比较了)
for (j = x + 1; j < row && flag != 1; j++)
{
//有一个比它大的就不行
if(matrix[j][y] > minNum)
{
flag = 1;
break;
}
}
//当前列没有发现比当前的minNum大的数字
if(flag == 0)
{
ans[0] = minNum;
*returnSize = 1;
return ans;
}
}
*returnSize = 0;
return ans;
}
14.矩阵对角元素的和
int diagonalSum(int** mat, int matSize, int* matColSize)
{
int row = matSize;
int col = matColSize[0];
int i,j,sum = 0;
j = col-1;
//主对角线
for (i = 0; i < row; i++)
{
int num1 = mat[i][i];//主对角线
int num2 = mat[i][j];//副对角线
//比较其是否是一个位置
if(i != j)
{
sum += num1 + num2;
}
else
{
sum += num1;
}
j--;//去前一列
}
return sum;
}
15.二进制矩阵中的特殊位置
(1)暴力
就是直接在矩阵中找到1的位置,然后再这里对其上下左右全部遍历,看看是否是唯一的1
int numSpecial(int** mat, int matSize, int* matColSize)
{
int row = matSize,col = matColSize[0];
int i,j,count = 0;
for (i = 0; i < row; i++)
{
for (j = 0; j < col; j++)
{
//找到1
if(mat[i][j] == 1)
{
int k = i;
bool flag = true;
//先找上面
for (k = i -1; k >= 0; k--)
{
if(mat[k][j] == 1)
{
printf("%d,%d",k,j);
flag = false;
break;
}
}
//下
for (k = i + 1; k < row && flag == true; k++)
{
if(mat[k][j] == 1)
{
flag = false;
break;
}
}
//左边
for(k = j - 1; k >= 0 && flag == true; k--)
{
if(mat[i][k] == 1)
{
flag = false;
break;
}
}
//右边
for(k = j + 1; k < col && flag == true; k++)
{
if(mat[i][k] == 1)
{
flag = false;
break;
}
}
if(flag == true)
{
count++;
}
}
}
}
return count;
}
(2)模拟
int numSpecial(int** mat, int matSize, int* matColSize)
{
int row = matSize;
int col = matColSize[0];
int i,j,count = 0;
//记录每一行,每一列的1的个数
int* rowSum = (int*)calloc(row, sizeof(int));
int* colSum = (int*)calloc(col, sizeof(int));
for (i = 0; i < row; i++)
{
for (j = 0; j < col; j++)
{
rowSum[i] += mat[i][j];
colSum[j] += mat[i][j];
}
}
for (i = 0; i < row; i++)
{
for (j = 0; j < col; j++)
{
if(mat[i][j] == 1 && rowSum[i] == 1 && colSum[j] == 1)
{
count++;
}
}
}
return count;
}
16.最富有客户的资产总量
- 求出每一行的总和,选出最大的即可
int maximumWealth(int** accounts, int accountsSize, int* accountsColSize)
{
int row = accountsSize,col = accountsColSize[0];
int i,j,ans = INT_MIN;
for (i = 0; i < row; i++)
{
int sum = 0;
for (j = 0; j < col; j++)
{
sum += accounts[i][j];
}
if(sum > ans)
{
ans = sum;
}
}
return ans;
}
17.判断矩阵经轮转后是否一致

额。。。。。。做吧和上一题一样,一转一个不吱声 /(ㄒoㄒ)/~~
还以为有什么简单办法,题解也全是在各种转。
题目中没有1 2 3 这是我自己写的,题目中的第一行全是0 0 0 所以导致在比较的时候可能会忽视一些细节上的东西,就是第一个和谁去比较,和红色的去比较。
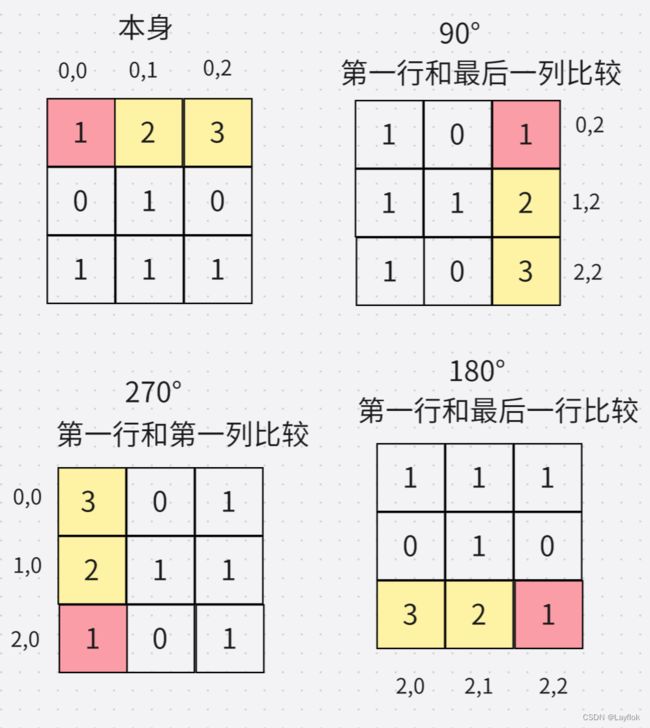
bool findRotation(int** mat, int matSize, int* matColSize, int** target, int targetSize, int* targetColSize)
{
int row = matSize,col = matColSize[0];
bool flag_0 = true,flag_90 = true,flag_180 = true, flag_270 = true;
int i,j;
for (i = 0; i < row; i++)
{
for (j = 0; j < col; j++)
{
int tmp = mat[i][j];
//没有转
if(tmp != target[i][j])
{
flag_0 = false;
}
//90°
if(tmp != target[j][col - 1 - i])
{
flag_90 = false;
}
//180°
if(tmp != target[row - 1 - i][col - 1 - j])
{
flag_180 = false;
}
//270°
if(tmp != target[row - 1 - j][i])
{
flag_270 = false;
}
}
}
return flag_0 || flag_90 || flag_180 || flag_270;
}
18.将一维数组转变成二维数组
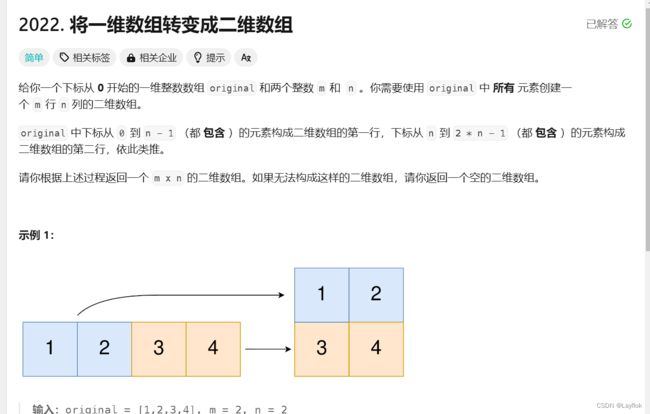
在前面的第二题重塑矩阵当中,是两个矩阵之间的转化,长这样子的。

这个思路很好的,也可以运用到一维转二维当中去。当我们会这个公式,那么做这道题就不难了
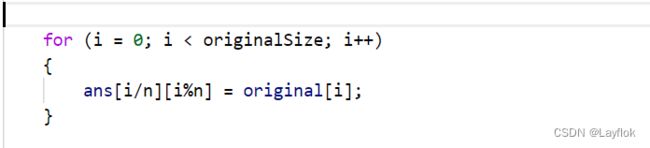
当你确定好行和列的时候,你就可以直接套用这个公式
int** construct2DArray(int* original, int originalSize, int m, int n, int* returnSize, int** returnColumnSizes)
{
int i;
int** ans = (int**)malloc(sizeof(int*) * m);
*returnColumnSizes = (int*)malloc(sizeof(int) * m);
for (i = 0; i < m; i++)
{
(*returnColumnSizes)[i] = n;
ans[i] = (int*)malloc(sizeof(int) * n);
}
if(originalSize != m * n)
{
(*returnColumnSizes)[0] = 0;
*returnSize = 0;
return ans;
}
for (i = 0; i < originalSize; i++)
{
ans[i/n][i%n] = original[i];
}
*returnSize = m;
return ans;
}
优化
在这个基础上,也可以优化一下,这是一个数一个数的去拷贝,当知道每行有 n 个的时候,可以利用memcpy函数直接拷贝n个进去

而代码就是把这个两个for循环替换一下就好了
19.检查是否每一行每一列都包含全部的整数

因为是 1 ~ n 的整数,所有只要不是全部出现,他就是一定出现重复的数字
- 那一个哈希表,去遍历它的每一行,每一列,然后记录
- 当发现出现重复的时候,直接return false就好了
bool checkValid(int** matrix, int matrixSize, int* matrixColSize)
{
int row = matrixSize,col = matrixColSize[0];
int* map = (int*)calloc(row + 1, sizeof(int));
int i,j;
//行
for (i = 0; i < row; i++)
{
for (j = 0; j < col; j++)
{
int key = matrix[i][j];
if(map[key] != 0)
{
return false;
}
map[key]++;
}
memset(map,0,sizeof(int) * (row+1)); //每一行完了重置
}
//列
for (i = 0; i < row; i++)
{
for (j = 0; j < col; j++)
{
int key = matrix[j][i];
if(map[key] != 0)
{
return false;
}
map[key]++;
}
memset(map,0,sizeof(int) * (row+1)); //每一列完了重置
}
return true;
}
20.判断矩阵是否是一个X矩阵
- 遍历矩阵,把两种情况设出来即可
bool checkXMatrix(int** grid, int gridSize, int* gridColSize)
{
int row = gridSize, col = gridColSize[0];
int i,j;
for (i = 0; i < row; i++)
{
for (j = 0; j < col; j++)
{
//主对角线 或者 是副对角线
if(i == j || j == col - 1 - i)
{
if(grid[i][j] == 0)
{
return false;
}
}
else
{
if(grid[i][j] != 0)
{
return false;
}
}
}
}
return true;
}
21.矩阵中的局部最大值

这道题,首先得知道要是9宫格,那么你遍历矩阵的时候,就不能还是老老实实的从第一行第一个元素开始遍历了,看下图,自身元素能产生就9宫格的,只能从第二行第二列开始遍历,结尾也得注意。
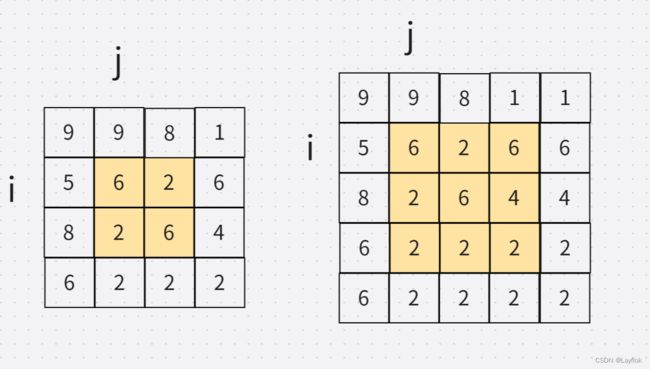
既然有了9宫格的范围,确保不会越界时候,就是获取其中最大的元素,将其记录到一个数组中去
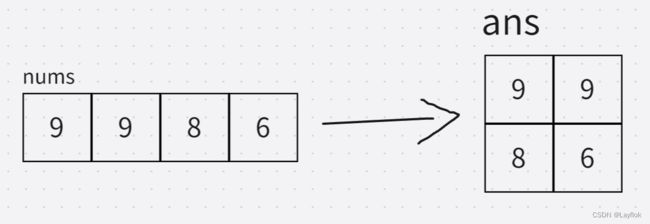
而将一位数组转化为二维数组,上面也做过。
下面代码中有注释
int** largestLocal(int** grid, int gridSize, int* gridColSize, int* returnSize, int** returnColumnSizes)
{
int row = gridSize, col = gridColSize[0];
int n = row - 2;
int i,j;
//返回一个n * n 的矩阵
int** ans = (int**)malloc(sizeof(int*) * n);
*returnSize = n;
*returnColumnSizes = (int*)malloc(sizeof(int) * n);
for (i = 0; i < n; i++)
{
(*returnColumnSizes)[i] = n;
ans[i] = (int*)malloc(sizeof(int) * n);
}
//最大值序列数组
int* nums = (int*)malloc(sizeof(int) * n * n);
int index = 0; //index 是nums 数组的索引
//九宫格方位移动坐标
int coordX[8] = {-1,-1,-1,0,1,1,1,0};
int coordY[8] = {-1,0,1,1,1,0,-1,-1};
for (i = 1; i < row - 1; i++)
{
for (j = 1; j < col - 1; j++)
{
//假设最大的是中心点
int maxNum = grid[i][j];
int k;
//找出当前9宫格内的最大值
for (k = 0; k < 8; k++)
{
int dx = i + coordX[k];
int dy = j + coordY[k];
if(grid[dx][dy] > maxNum)
{
maxNum = grid[dx][dy];
}
}
//将最大值序列先录入nums数组中去
nums[index++] = maxNum;
}
}
//将nums数组转化为矩阵
for (i = 0; i < index; i++)
{
ans[i/n][i%n] = nums[i];
}
return ans;
}
22.删除每行中的最大值
- 将矩阵的每一行进行排序(具体看自己是选择升序还是降序)
- 总会出现有一列是每一行最大的数
- 然后去这一列中找到那个最大的数,将其加入到sum中去即可
int cmp_int(const void* x, const void* y)
{
return *(int*)x - *(int*)y;
}
int deleteGreatestValue(int** grid, int gridSize, int* gridColSize)
{
int row = gridSize,col = gridColSize[0];
int i,j,sum = 0,n = col - 1;
//对矩阵每一行进行排序
for (i = 0; i < row; i++)
{
qsort(grid[i],col,sizeof(int),cmp_int);
}
//n 为每行最大值的下标
while(n >= 0)
{
//去n所在列最大值
int maxNum = grid[0][n];
for (i = 1; i < row; i++)
{
if(grid[i][n] > maxNum)
{
maxNum = grid[i][n];
}
}
sum += maxNum;
n--;
}
return sum;
}
23.对角线上的质数

前面那么题都有遍历对角线的知识,这里还是老办法去遍历对角线。
- 判断对角线数是否是质数
- 更新最大值
要注意,使用一般的判断质数的方式会超时的,用遍历到平方根的不会超时
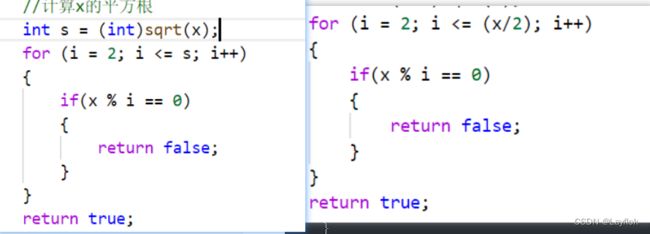
bool IsPrimeNum(int x)
{
if(x < 2)
{
return false;
}
int i;
//计算x的平方根
int s = (int)sqrt(x);
for (i = 2; i <= s; i++)
{
if(x % i == 0)
{
return false;
}
}
return true;
}
int Max(int x,int y)
{
return x > y ? x : y;
}
int diagonalPrime(int** nums, int numsSize, int* numsColSize)
{
int row = numsSize, col = numsColSize[0];
int i,j,ans = 0;
for (i = 0; i < row; i++)
{
//主对角
if(IsPrimeNum(nums[i][i]))
ans = Max(nums[i][i],ans);
//副对角
if(IsPrimeNum(nums[i][col - 1 - i]))
ans = Max(nums[i][col - 1 - i],ans);
}
return ans;
}
24.查询网格图中每一列的宽度
- 设计一个函数,可以获取一个整数的长度。
- 这个函数对于负数来说,多加一个长度即可
- 然后去按列去遍历。一列一列的去
//传过一个数子来,求出他的宽度
int SolveWight(int x)
{
int wight = 0;
//负数的话,先将其负号算上
if(x <= 0)
{
wight++;
wight = abs(wight);
}
while(x != 0)
{
x /= 10;
wight++;
}
return wight;
}
int* findColumnWidth(int** grid, int gridSize, int* gridColSize, int* returnSize)
{
int row = gridSize, col = gridColSize[0];
int i,j;
int* ans = (int*)malloc(sizeof(int) * col);
//按照列去遍历
for (i = 0; i < col; i++)
{
int maxWight = 0;
for (j = 0; j < row; j++)
{
int wight = SolveWight(grid[j][i]);
if(wight > maxWight)
{
maxWight = wight;
}
}
ans[i] = maxWight;
}
*returnSize = col;
return ans;
}
25.一最多的行
- 对矩阵进行遍历,遍历其每一行,
- 然后对每一行都求出其1出现次数
- 与出现最多的次数进行比较
- 不断的更新
int* rowAndMaximumOnes(int** mat, int matSize, int* matColSize, int* returnSize)
{
int* ans = (int*)malloc(sizeof(int) * 2);
*returnSize = 2;
int row = matSize, col = matColSize[0];
int i,j;
int maxCount = INT_MIN;
for (i = 0; i < row; i++)
{
int count = 0;
for (j = 0; j < col; j++)
{
count += mat[i][j];
}
//更新出现最多的次数以及下标
if(count > maxCount)
{
maxCount = count;
ans[0] = i;
ans[1] = maxCount;
}
}
return ans;
}
26.找到冠军
这道题,如果和上题一样,直接统计出出现1最多的哪一行也是可以过的。
那这道题的意义在哪儿呢。。。。
- 最强的那个队伍,除了和自身相比,其余的全胜
- 也就是说出来grid[i][i] = 0 其余的全是1,所以1的个数是col-1.
int findChampion(int** grid, int gridSize, int* gridColSize)
{
int row = gridSize, col = gridColSize[0];
int i,j;
for (i = 0; i < row; i++)
{
int count = 0;
for (j = 0; j < col; j++)
{
count += grid[i][j];
}
//最强的队伍,除了和自身相比,剩下的全是1
if(count == col - 1)
{
return i;
}
}
return 0;
}
27.循环移位后的矩阵相似检查
bool areSimilar(int** mat, int matSize, int* matColSize, int k)
{
int row = matSize,col = matColSize[0];
int i,j;
for (i = 0; i < row; i++)
{
for (j = 0; j < col; j++)
{
int l = j + k;
if(mat[i][j] != mat[i][l % col])
{
return false;
}
}
}
return true;
}
28.找出缺失和重复的数字
- 遍历矩阵,用哈希表存储每个数字出现的次数
- 然后去遍历哈希表,找出重复出现的和缺失的数字即可。
int* findMissingAndRepeatedValues(int** grid, int gridSize, int* gridColSize, int* returnSize)
{
int row = gridSize, col = gridColSize[0];
int i,j,n = row * col;
int* map = (int*)calloc(n + 1,sizeof(int));
int* ans = (int*)malloc(sizeof(int) * 2);
//遍历矩阵,然后记录每个数出现的次数
for (i = 0; i < row; i++)
{
for (j = 0; j < col; j++)
{
int key = grid[i][j];
map[key]++;
}
}
//值的范围是[1,n]
for (i = 1; i <= n; i++)
{
//重复
if(map[i] == 2)
{
ans[0] = i;
}
//缺失
if(map[i] == 0)
{
ans[1] = i;
}
}
*returnSize = 2;
return ans;
}
29.无人机方阵

我如果用哈希表记录第一个矩阵中出现各个数据出现的次数,
然后遍历第二个矩阵的时候去查哈希表,如果哈希表中没有出现,那么答案就该增加1么。
图有点潦草。。但是这样子做不对,测试用例给的太多了,也看不出来!!!有懂的欢迎评论
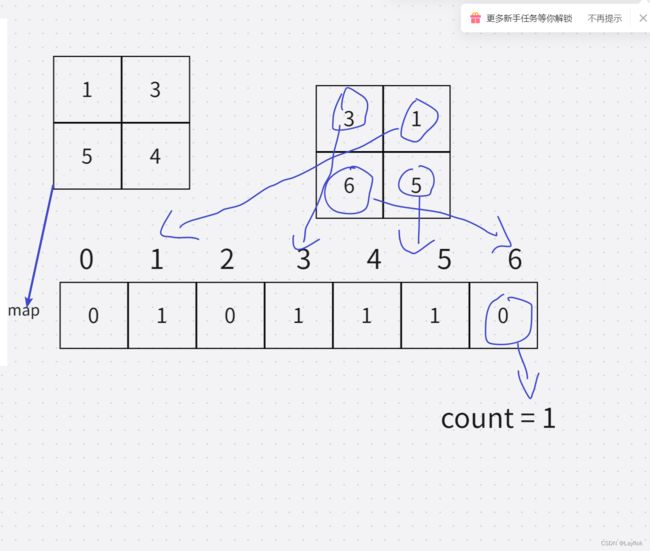
题解如下:
#define LEN 10001
int minimumSwitchingTimes(int** source, int sourceSize, int* sourceColSize, int** target, int targetSize, int* targetColSize){
int map1[LEN] = { 0 };
int map2[LEN] = { 0 };
for (int i = 0; i < sourceSize; i++)
{
for (int j = 0; j < *sourceColSize; j++)
{
map1[source[i][j]] += 1;
map2[target[i][j]] += 1;
}
}
// 变化后的灯光减去变化前的灯光
int sum = 0;
for (int i = 0; i < LEN; i++)
{
if (map2[i] - map1[i] > 0)
{
sum += map2[i] - map1[i];
}
}
return sum;
}