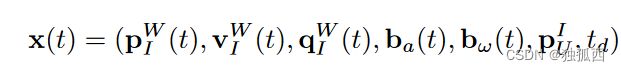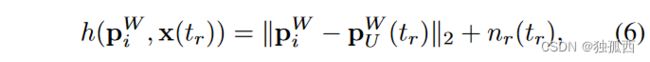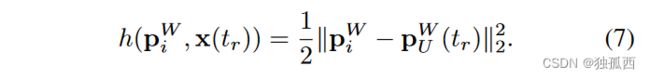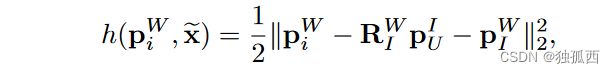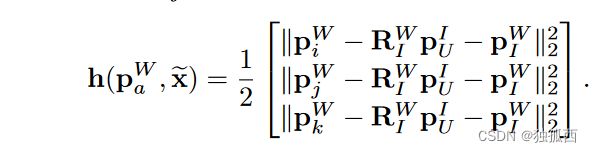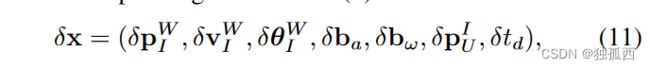论文阅读:Online Spatio-temporal Calibration of Tightly-coupled Ultrawideband-aided Inertial Localization
前言
Online Spatio-temporal Calibration of Tightly-coupled Ultrawideband-aided Inertial Localization这篇论文是发布在IROS2021上的一篇文章,主要针对载体上的MU和UWB进行空间校准与时间校准。
一、问题背景
GPS拒止:在室内环境中缺乏一种有效的定位方案,并且在城市峡谷中GPS性能会显著下降。基于相机IMU的定位系统的可靠运行需要良好的光照、持久和可区分的特征、闭环以及场景的主要部分是静态和无遮挡的。在仓库、工厂、医院和商场等高度动态的环境中,这些需求可以是限制性的。
空间偏移:通常,IMU和UWB无线电不是共址的,两个传感器之间存在空间偏移,也称为传感器外部参数。目前的校准技术涉及手动测量空间偏移,使用测量设备或额外的传感器。这些方法容易出错且价格昂贵。虽然计算机辅助图提供了收音机的机械规格,但相位中心1的准确位置通常是不知道的。
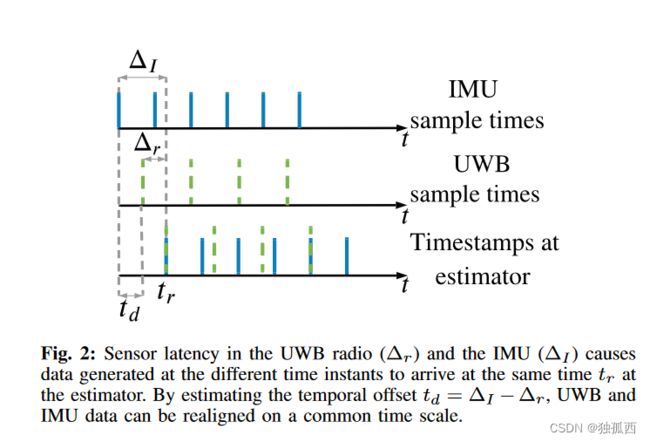
时间偏移:我们的设置要求IMU和UWB数据相对于单一的时钟源具有精确的时间戳。这一般是通过使用共同的时钟信号进行硬件同步来实现的。下一个最佳选择是使用运行在目标计算机上的时钟服务器和传感器硬件上的客户端进行软件同步。然而,许多现成的组件并不支持这两种方法。因此,由于传感器延迟和不同的时钟源,来自异构传感器的数据之间存在时间偏移,如图2所示。在不对时空偏移进行补偿的情况下进行状态估计会导致较差的定位精度,特别是当这些偏移较大时。
UWB-IMU模型:以往的大多数工作要么假设已知的空间偏移参数,要么仅使用额外的硬件校准空间偏移。紧耦合UWB - IMU系统的测量是距离测量,而不是位姿测量。针对相机- IMU系统提出的标定方法不适用于本文所考虑的系统。以前的很多工作都校准了空间偏移或时间偏移,但不是两者都校准。此外,正如先前所述,松散耦合的系统具有局限性。据作者所知,尚未对紧耦合UWB - IMU系统进行联合时空标定。由于紧耦合UWB - IMU系统的观测模型不同于相机- IMU系统的观测模型,文献[ 10 ]、[ 13 ]中的分析在此不再直接适用。在[ 15 ]中,我们证明了仅有空间偏移的松耦合GPS - IMU系统的线性近似的可观测性。相反,在没有任何近似的情况下,我们推导出了紧耦合UWB - IMU系统状态和空间偏移的局部弱可观测性的条件。我们还推导了这样一个系统的时间偏移量是局部可识别的条件。
二、主要假设
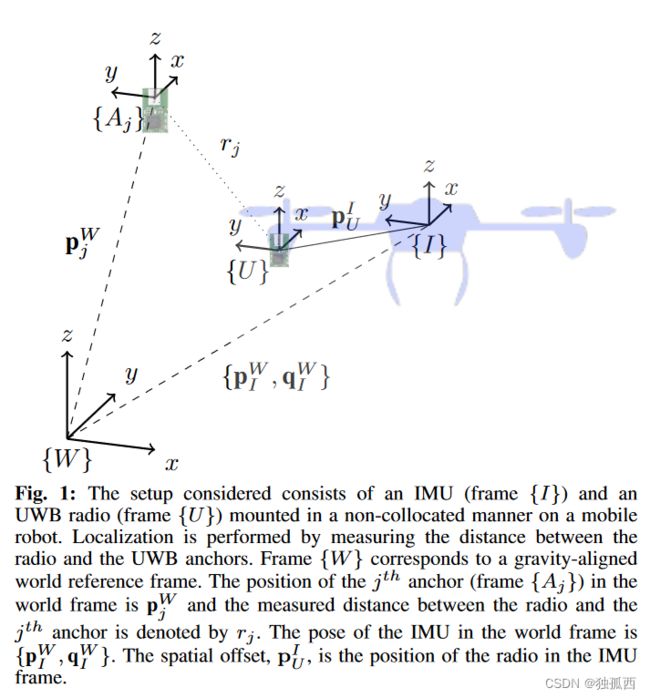
考虑如图所示的装置,其中,配备IMU和UWB无线电的系统通过测量其无线电和锚之间的TW - ToF来定位自身。
做出以下假设:
( A1 )空间偏移和时间偏移是恒定的,不随时间变化。
( A2 )将UWB无线电视为点源。因此,不考虑其方向性。
在这些假设下,校准目标是:
( O1 )建立紧耦合UWB - IMU系统在空间偏移局部弱可观测和时间偏移局部可辨识的条件;
( O2 )通过联合估计( i ) IMU的位置、方向和速度,( ii ) IMU的偏差,( iii ) UWB - IMU的空间偏移和( iv ) UWB - IMU的时间偏移来提高定位精度。
三、理论流程
1、系统模型
系统通过如下20维状态向量描述:
其中前三个为IMU坐标系为载体中心的全局位置,使用四元数表示旋转;之后两个为IMU的零偏和噪声;最后两个是空间偏移(UWB接收器在IMU坐标系的位置)、时间偏移(如上图)。
陀螺仪和加速度计模型描述。。。
本工作中的运动模型是三维运动学运动模型,其中加速度计和陀螺仪的测量值用作控制输入:
在紧耦合系统中,观测模型为锚与移动电台之间的距离。tr时刻到第i个锚点的测量距离是锚点位置p Wi和状态x ( tr )的函数:
其中锚点全局位置为:
本文采用UWB时间戳作为参考时间。计算式( 6 )需要状态( 1 )在时刻tr的值。设tr也是最近一次IMU测量的时间戳。值得注意的是,由于时间偏移td的存在,IMU测量值相对于UWB时间戳(见图2)实际产生于时间tI = tr - td。为了计算时刻tr的状态,我们使用运动模型( 2 ) - ( 5 )和从tI开始的IMU测量( s )将时刻tI的状态传播td秒。注意td可以是正的也可以是负的。
2、可观测性和可识别性分析
可观测性分析的目的是检查在给定系统输出的情况下,系统的状态是否可以唯一确定。我们将状态( 1 )的可观测性问题分解为
( i ) td的局部可识别性[ 6 ]和
( ii )不含td的部分状态的局部弱可观测性[ 5 ] .
[5] Robert Hermann and Arthur J Krener. Nonlinear controllability and observability. IEEE Transactions on Automatic Control, (5), 1977.
[6] Milena Anguelova and Bernt Wennberg. State elimination and identifiability of the delay parameter for nonlinear time-delay systems. Automatica, 44(5):1373–1378, 2008.
下面给出这一两步过程的动机和理由。
在[ 6 ]中,证明了单个未知常时滞的可辨识性可以独立于状态的可观测性进行分析。作者指出,非线性系统中时滞的可辨识性与其他系统状态或参数的可观测性没有直接关系。具体来说,时滞参数可以直接从系统的输入-输出表示[ 6 ]中确定,该表示仅依赖于系统的输入、输出及其时间导数。因此,时滞的局部可辨识性等价于确定一个输入输出表示是否存在。对于一般的非线性系统,要找到这样的输入输出表示是很困难的。然而,非线性系统存在输入输出表示的一个充要条件是在输出( 6 ) (文献中的定理2)中出现延迟输入变量(在我们的情况下am和ω m) .我们使用这种方法来分析td的局部可识别性。
正如文献[ 6 ]所指出的,时滞的可辨识性并不意味着状态的可观测性。在证明了td的局部可辨识性之后,我们分析了不含td的部分状态的可观测性,即" x = ( pW I , vW I , qW I , ba , bω , pI U) "。为此,我们采用文献[ 5 ]中的方法,该方法涉及确定可观性矩阵O的秩[ 5 ]。文献[ 6 ]和[ 5 ]中的方法考虑了无噪声的非线性系统的情形。因此,在接下来的分析中,我们忽略了噪声参数的影响。
(1)时间偏移的局部可识别性
根据[ 6 ],td的局部可识别性取决于它是否存在于系统( 2 ) - ( 5 )和( 6 )的输入输出表示中,即在输出函数中存在延迟输入变量( s )。在我们的案例中,足以说明am( tr-td)或ω m( tr-td)出现在测量模型中。不失一般性,计量模型( 6 )可以写为:
我们考虑单个锚,因为对多个锚的分析是相同的。为了简化分析,引入了1 / 2因子。由于存在两个输入,如果am或ω m被激发,td可以被局部识别。在下面的定理中,我们陈述了td局部可识别的条件:
(2)紧耦合UWB - IMU系统的可观测性
现在我们分析" x "的可观测性。系统动力学( 2 ) - ( 5 )被重新排列成控制仿射形式[ 5 ]:
不失一般性,计量模型( 6 )可以改写为:
其中,为简洁起见,我们去掉对时间的依赖,将p W U展开为p W U = R W I p I U + p W I。为了简化分析,引入了1 / 2因子。来自单个锚的测量不足以约束整个状态。因此,我们考虑使用三个锚点进行测量:
为了证明状态是局部可观测的,我们需要确定与系统( 8 ) - ( 9 )相关的可观测性矩阵O [ 5 ]的秩。矩阵O是通过沿系统动力学( 8 )取( 9 )的李导数[ 5 ]构造的。通常,Lie导数计算系统状态变化时系统输出的变化。因此,O映射为状态的变化到输出的变化。如果矩阵O具有满列秩,那么它可以被反转,并用于将输出的变化映射为状态的变化。在下面的定理中,我们陈述了系统( 8 ) - ( 9 )是局部弱可观的条件。
3、估计
前一部分的分析表明,在一定条件下,状态( 1 )可以被可靠地估计.然而,一个合适的状态估计器的设计或选择不能从这样的分析中得到。在这一部分中,我们提出了一种可用于紧耦合UWB - IMU系统的时空校准方法。估计器的选择是基于其对非线性系统的适用性,计算效率和对稀疏传感器数据的操作能力。
为了同时估计状态和校准时空偏移参数,我们使用ESKF [ 17 ]。在这个公式中,惯性航位推算使用模型( 8 )和IMU测量值作为输入,将状态( 1 )在时间上向前传播。在预测步骤中估计与航位推算相关的不确定性。在校正步骤中,利用UWB测量值的不确定度,通过融合死区估计状态和UWB测量值来估计误差及其不确定度。与状态( 1 )相对应的错误状态是:
参考[ 18 ]来描述ESKF的预测和校正步骤。过程噪声矩阵Qp和测量噪声矩阵Qr的协方差值由第七节- B节的方法确定
[17] Stergios I. Roumeliotis, Gaurav S. Sukhatme, and George A. Bekey. Circumventing dynamic modeling: evaluation of the error-state Kalman filter applied to mobile robot localization. In Proc. of the IEEE International Conference on Robotics and Automation (ICRA), pages 1656–1663 vol.2, 1999.
[18] J. Sol` a. Quaternion kinematics for the error-state Kalman filter. ArXiv, abs/1711.02508, 2017.
四、实验方案
1、模拟实验
我们的仿真环境基于Gazebo [ 20 ]。四旋翼飞行器配备了UWB无线电和IMU。锚杆采用固定无线电台模拟。UWB无线电的距离测量受到零均值AWGN的干扰,其标准差为2cm。噪声参数的选择是基于市场上现有的UWB电台的精度[ 22 ]。
[20] N. Koenig and A. Howard. Design and use paradigms for Gazebo, an open-source multi-robot simulator. In 2004 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS) (IEEE Cat. No.04CH37566), volume 3, pages 2149–2154 vol.3, 2004.
[22] Humatics Rail Navigation System datasheet. https://humatics.com/wpcontent/uploads/2020/07/Humatics RailNav Datasheet 072020.pdf.
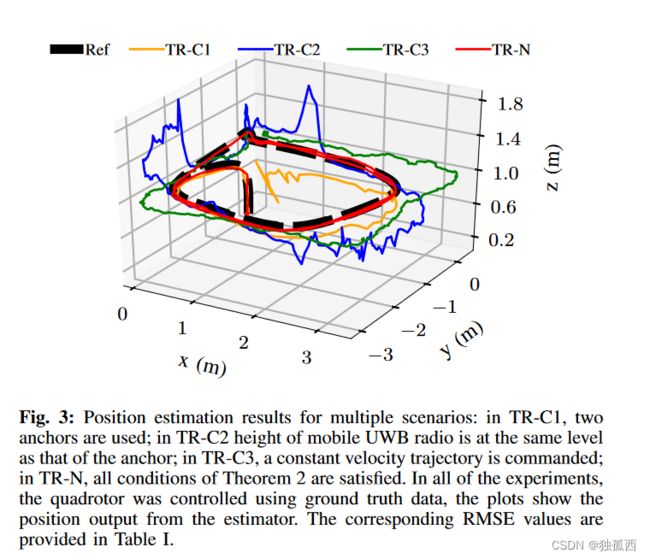
为了验证第5节所述的可观测性和可辨识性条件,我们进行了多次仿真实验,其中我们改变了( i )锚点的数量,( ii )锚点的高度,( iii )四旋翼飞行器的速度分布。在所有的实验中,地面真实数据被用于四旋翼飞行器的控制。状态估计器估计的位置如图3所示,相应的误差指标如表1所示。
每个实验都违反了定理2中的一个条件;
实验TR - C1违反条件C1,即使用两个锚点进行估计;
在TR - C2中,调整锚点高度,使移动电台的飞行轨迹ry与锚点共面;
在TR - C3中,指令一个加速度计和陀螺仪轴激励不足的恒速飞行轨迹ry;
在TR - N中,定理2中的所有条件都满足.
在TR - C1中,由于锚点不足,定位逐渐发散;
在TR - C2中,矩阵( 10 )中第3列为零,导致沿z轴的位置估计较差;
在TR - C3中,估计的偏航发散,导致在xy平面内定位较差;
在TR - N中,估计的飞行轨迹与指挥的飞行轨迹接近。
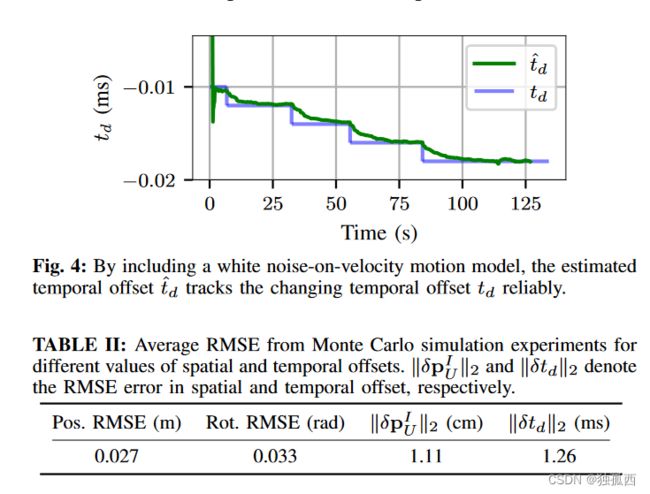
为了测试所提出的估计方法的稳定性,我们对UWB - IMU空间偏移量在- 0.5 ~ 0.5 m之间和时间偏移量在- 25 ~ 25 ms之间变化进行了蒙特卡洛( Monte Carlo,MC )仿真,结果如表2。
时间偏移可能在移动系统从启动到启动,或者在其运行的整个过程中都是不同的。这种情况可以通过使用随机游走模型来调节,其中Qd可以通过估计的时间偏移的Allan图[ 23 ]经验性地确定。本实验的设置与图3中TR - N的设置相同。在模拟过程中,td的值是动态变化的。所提出的模型能够估计变化的td,如图4所示。
为了全面量化空间和时间偏移误差对位置和旋转RMSE的影响,我们在不估计时空偏移的情况下,通过对参数进行扰动并记录相应的RMSE值进行了多次实验。结果如图5所示:对于较大的空间偏移,参数误差的影响更为突出。
2、真实实验
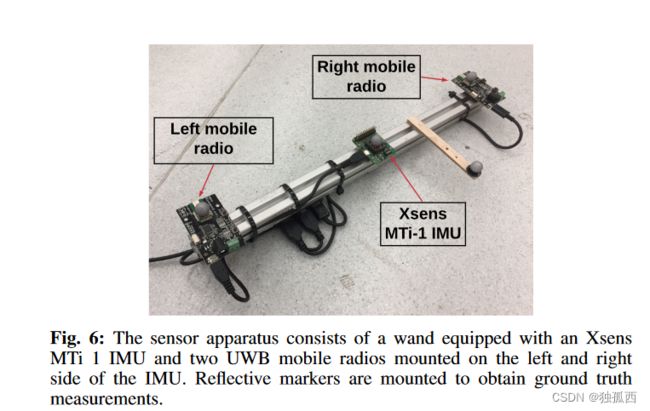
装置由传感器Wand (见图)、6个锚节点组成的星座和运动捕捉系统组成。接下来,我们描述了锚点位置的校准,紧接着描述了传感器杆。UWB定位系统的一个好处是,锚点位置的校准可以独立于移动系统(或者在我们的例子中, wand)来完成。锚跨距离可以通过配置一个锚点作为接收器,其余锚点作为发射器来获得。通过选择其中一个锚框作为原点,其余锚框的位置可以使用锚跨距离[ 24 ],[ 25 ]来确定。本文所采用的方法与[ 25 ]类似。
每次实验开始时,将传感器光棒静置60s,以产生陀螺仪和加速度计零偏的初始估计值。此外,使用静态数据通过平均加速度计报告的重力向量来生成对横滚和俯仰值的初始估计。IMU的位置通过将魔杖放置在世界框架的原点进行初始化。值得注意的是,这不是一个精确的初始化例程,初始姿态中的代表性不确定性被初始协方差捕获。根据第五节,通过各种旋转和平移机动来手动移动传感器杆,以试图模拟状态局部弱可观测的充分条件.
3、结果分析
我们进行了多组实验,证明了当满足定理1和定理2中的充分条件时,空间和时间偏移的联合校准是可能的,同时也是局部化的。由于篇幅限制,这里仅给出左侧移动电台的结果。右侧移动电台的结果与此类似。由于空间和时间偏移量的真实值不可得,我们通过计算偏移量的手测( HM )和自校准( SC )值的位置和旋转均方根误差( RMSE )来评估本文方法的精度。
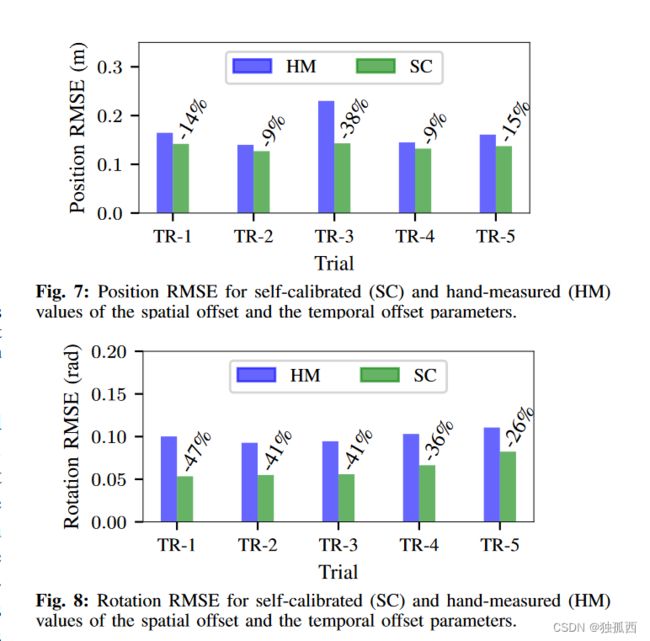
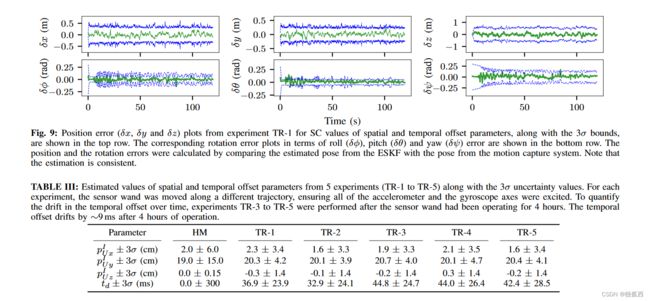
空间偏移的HM值是通过使用尺子手动测量IMU和UWB无线电之间的位置偏移量获得的。时间偏移参数被初始化为零。对于每次实验( TR-1 ~ TR-5),传感器棒沿不同的轨迹手动移动。标定结果如表III所示。通过比较从ESKF估计的位姿和从运动捕捉系统获得的地面真实位姿,计算估计位置和旋转的误差。TR - 1的SC参数值的位置和旋转误差图,以及3 σ协方差包络图,如图9所示。与HM值相比,SC偏移值的位置和旋转RMSE分别降低,如图7和图8所示。
为了量化时间偏移随时间的漂移,在传感器工作4小时后进行了TR3到TR - 5的实验。由表3可知,工作4 h后,时间偏移漂移量为Δ Δ 9 ms。这些结果是很有前途的,特别是由于UWB测量的精度( ± 10cm )与估计的空间偏移量( ~ 20cm )在数量级上是相似的。此外,RMSE值的降低与仿真实验的结果一致。对于20厘米基线,图5显示空间偏移2厘米误差使位置RMSE增加18 %,时间偏移30毫秒误差使旋转RMSE增加40 %。从图7和图8的结果可以看出,位置均方根误差平均降低了17 %,空间o改善了2 cm。
五、创新总结
本文推导了紧耦合UWB - IMU系统( i )空间偏移量的局部弱可观测性和( ii )时间偏移量的局部可辨识性的条件。提出了一种基于ESKF的在线标定方法。仿真和真实世界实验的结果表明,如果满足可观测性和可识别性条件,就可以准确地校准空间偏移和时间偏移,同时无需额外的传感器或硬件进行定位,从而不需要单独的校准程序。由于UWB无线电和摄像头具有互补的特性,在UWB-IMU系统中加入摄像头可以提供许多优点。这种系统的时空标定可以看作是本文工作的自然延伸。
在本文中,我们进行了可观测性分析,以导出内部状态和空间偏移的局部弱可观测性[ 5 ]的条件。利用一个相关的性质,局部可识别性[ 6 ],我们得到了时间偏移是局部可识别的条件。可观测性分析有助于我们回答一个特定的系统及其状态是否可观测的问题。然而,它并不适合设计一个合适的估计器,特别是在噪声存在的情况下。在这项工作中,我们提出了一种基于误差状态卡尔曼滤波( ESKF )的在线方法来联合估计状态和空间和时间偏移参数。概括起来,我们的主要贡献如下:
1)我们推导出了时间偏移是局部可识别的条件;
2 ) 推导了包含空间传感器偏差在内的紧耦合UWB - IMU系统状态局部弱可观测的条件;
3 ) 提供了一种估计紧组合IMU位置、姿态、速度、IMU偏差、空间偏差和时间偏差的统一方法
Uwb - Imu系统;
4 ) 我们在模拟和真实数据上对所提出的方法进行了评估,以验证我们的理论,并显示推荐方法的有效性。
本文的核心思想就是将空间偏移和时间偏移一起作为被估计量利用ESKF滤波器进行状态估计,不过本文创新之处在于分析了可观测性与可识别性,给出了对应条件,完善了UWB-IMU在线标定的工作。