PPP算法
学习rtklib的PPP模块，先对重要的算法进行原理性阐述
一、PPP原理
精密单点定位采用双频伪距观测值
、
和载波相位观测值
、
获得测点的三维位置。在基本观测方程的基础上，通常有三种模型，分别是传统的无电离层组合观测模型、UofC模型（半和模型）、以及非差非组合模型。
基本观测方程：
假定接收机i在
时刻接收到卫星j于
时刻发送的卫星信号，则对于载波相位观测值、和P码伪距观测值、,可建立观测方程：
L 1 r j ( t r ) = ρ ( t s , t r ) − c δ t j S + c δ t i R − I o n ∗ f 2 2 / ( f 1 2 − f 2 2 ) + δ T r o p i j + c N 1 i j / f 1 + ∑ δ L 1 {L_{1}}_{r}^{j}(t_{r})=\rho (t_{s},t_{r})-c\delta{t _{j}^{S}}+c\delta{t _{i}^{R}}-Ion*^{f_{2}^{2}}/({f_{1}^{2}}-{f_{2}^{2}})+\delta{Trop_{i}^{j}}+c{N_{1}}_{i}^{j}/f_{1}+\sum \delta _{L1} L1rj(tr)=ρ(ts,tr)−cδtjS+cδtiR−Ion∗f22/(f12−f22)+δTropij+cN1ij/f1+∑δL1
L 2 r j ( t r ) = ρ ( t s , t r ) − c δ t j S + c δ t i R − I o n ∗ f 1 2 / ( f 1 2 − f 2 2 ) + δ T r o p i j + c N 2 i j / f 2 + ∑ δ L 2 {L_{2}}_{r}^{j}(t_{r})=\rho (t_{s},t_{r})-c\delta{t _{j}^{S}}+c\delta{t _{i}^{R}}-Ion*^{f_{1}^{2}}/({f_{1}^{2}}-{f_{2}^{2}})+\delta{Trop_{i}^{j}}+c{N_{2}}_{i}^{j}/f_{2}+\sum \delta _{L2} L2rj(tr)=ρ(ts,tr)−cδtjS+cδtiR−Ion∗f12/(f12−f22)+δTropij+cN2ij/f2+∑δL2
P 1 r j ( t r ) = ρ ( t s , t r ) − c δ t j S + c δ t i R − I o n ∗ f 2 2 / ( f 1 1 − f 2 2 ) + + ∑ δ P 1 {P_{1}}_{r}^{j}(t_{r})=\rho (t_{s},t_{r})-c\delta{t _{j}^{S}}+c\delta{t _{i}^{R}}-Ion*^{f_{2}^{2}}/({f_{1}^{1}}-{f_{2}^{2}})++\sum \delta _{P1} P1rj(tr)=ρ(ts,tr)−cδtjS+cδtiR−Ion∗f22/(f11−f22)++∑δP1
P 2 r j ( t r ) = ρ ( t s , t r ) − c δ t j S + c δ t i R − I o n ∗ f 1 2 / ( f 1 2 − f 2 2 ) + δ T r o p i j + ∑ δ P 2 {P_{2}}_{r}^{j}(t_{r})=\rho (t_{s},t_{r})-c\delta{t _{j}^{S}}+c\delta{t _{i}^{R}}-Ion*^{f_{1}^{2}}/({f_{1}^{2}}-{f_{2}^{2}})+\delta{Trop_{i}^{j}}+\sum \delta _{P2} P2rj(tr)=ρ(ts,tr)−cδtjS+cδtiR−Ion∗f12/(f12−f22)+δTropij+∑δP2
式中，
为卫星到接收机的几何距离，c为真空中的光速，
为卫星j在信号发射时刻相对于GPS时间的钟差，
为接收机i在信号接收时刻相对于GPS时间的钟差，Ion为电离层延迟参数，
为对流层延迟改正，
为L1载波整周模糊度，
为L2载波整周模糊度，
为其他必须顾及的改正，如天线相位中心改正、天线相位缠绕、地球固体潮改正、大洋负荷改正、引力延迟改正、相对论效应改正等。
1、传统无电离层组合模型
卫星信号所收到的电离层延迟影响与频率的平方成反比，利用这一性质，可将伪距观测值、和载波相位观测值、组合成合适的组合观测值，消除电离层影响：
L I F i j ( t r ) = f 1 2 / ( f 1 2 − f 2 2 ) ∗ L 1 i j ( t r ) − f 2 2 / ( f 1 2 − f 2 2 ) ∗ L 2 i j ( t r ) = ρ ( t s , t r ) − c δ t j S + c δ T r o p i j + λ I F N I o n − F r e e i j + ∑ δ L I F {L_{IF}}_{i}^{j}(t_{r})=f_{1}^{2}/(f_{1}^{2}-f_{2}^{2})*{L_{1}}_{i}^{j}(t_{r})-f_{2}^{2}/(f_{1}^{2}-f_{2}^{2})*{L_{2}}_{i}^{j}(t_{r})=\rho (t_{s},t_{r})-c\delta t_{j}^{S}+c\delta Trop_{i}^{j}+\lambda _{IF}{N_{Ion-Free}}_{i}^{j}+\sum \delta _{L_{IF}} LIFij(tr)=f12/(f12−f22)∗L1ij(tr)−f22/(f12−f22)∗L2ij(tr)=ρ(ts,tr)−cδtjS+cδTropij+λIFNIon−Freeij+∑δLIF
P I F i j ( t r ) = f 1 2 / ( f 1 2 − f 2 2 ) ∗ P 1 i j ( t r ) − f 2 2 / ( f 1 2 − f 2 2 ) ∗ P 2 i j ( t r ) = ρ ( t s , t r ) − c δ t j S + c δ T r o p i j + ∑ δ P I F {P_{IF}}_{i}^{j}(t_{r})=f_{1}^{2}/(f_{1}^{2}-f_{2}^{2})*{P_{1}}_{i}^{j}(t_{r})-f_{2}^{2}/(f_{1}^{2}-f_{2}^{2})*{P_{2}}_{i}^{j}(t_{r})=\rho (t_{s},t_{r})-c\delta t_{j}^{S}+c\delta Trop_{i}^{j}+\sum \delta _{P_{IF}} PIFij(tr)=f12/(f12−f22)∗P1ij(tr)−f22/(f12−f22)∗P2ij(tr)=ρ(ts,tr)−cδtjS+cδTropij+∑δPIF
式中，
和
分别为无电离层组合观测值的波长及模糊度，此时模糊度参数不再具有整周特性，即
λ I F = c f 1 / ( f 1 2 − f 2 2 ) \lambda _{IF}=cf_{1}/(f_{1}^{2}-f_{2}^{2}) λIF=cf1/(f12−f22)
N I F i j = N 1 i j − f 2 / f 1 ∗ N 2 i j {N_{IF}}_{i}^{j}={N_{1}}_{i}^{j}-f_{2}/f_{1}*{N_{2}}_{i}^{j} NIFij=N1ij−f2/f1∗N2ij
2、UofC模型（半和模型）
半和模型除了采用传统的无电离层载波相位组合观测值，还包括、频率上的P码/载波组合观测值，利用电离层影响在测码伪距方程和相位方程中的大小相等，互为相反数的性质。表达式如下：
L I F i j ( t r ) = f 1 2 / ( f 1 2 − f 2 2 ) ∗ L 1 i j ( t r ) − f 2 2 / ( f 1 2 − f 2 2 ) ∗ L 2 i j ( t r ) = ρ ( t s − t r ) − c δ t j S + c δ T r o p i j + λ I F N I o n − F r e e i j + ∑ δ L I F {L_{IF}}_{i}^{j}(t_{r})=f_{1}^{2}/(f_{1}^{2}-f_{2}^{2})*{L_{1}}_{i}^{j}(t_{r})-f_{2}^{2}/(f_{1}^{2}-f_{2}^{2})*{L_{2}}_{i}^{j}(t_{r})=\rho (t_{s}-t_{r})-c\delta t_{j}^{S}+c\delta Trop_{i}^{j}+\lambda _{IF}{N_{Ion-Free}}_{i}^{j}+\sum \delta _{L_{IF}} LIFij(tr)=f12/(f12−f22)∗L1ij(tr)−f22/(f12−f22)∗L2ij(tr)=ρ(ts−tr)−cδtjS+cδTropij+λIFNIon−Freeij+∑δLIF
P I F , L 2 i j ( t r ) = 1 / 2 ∗ ( P 2 i j ( t r ) + L 2 i j ( t r ) ) = ρ ( t s , t r ) − c δ t j S + c δ t i R + c δ T r o p i j + c N 1 i j / f 2 / 2 + ∑ δ P I F , L 2 {P_{IF,L_{2}}}_{i}^{j}(t_{r})=1/2*({P_{2}}_{i}^{j}(t_{r})+{L_{2}}_{i}^{j}(t_{r}))=\rho (t_{s},t_{r})-c\delta t_{j}^{S}+c\delta t_{i}^{R}+c\delta Trop_{i}^{j}+c{N_{1}}_{i}^{j}/f_{2}/2+\sum \delta _{P_{IF},L_{2}} PIF,L2ij(tr)=1/2∗(P2ij(tr)+L2ij(tr))=ρ(ts,tr)−cδtjS+cδtiR+cδTropij+cN1ij/f2/2+∑δPIF,L2
3、非差非组合模型
消电离层的组合观测方程不仅会造成一些有用信息的丢失，还会放大观测噪声，因此基于原始观测值的非差非组合模型显得尤为重要，trklib中一般采用非差非组合模型和无电离层模型。
L 1 r j ( t r ) = ρ ( t s , t r ) − c δ t j S + c δ t i R − I o n ∗ f 2 2 / ( f 1 2 − f 2 2 ) + δ T r o p i j + c N 1 i j / f 1 + ∑ δ L 1 {L_{1}}_{r}^{j}(t_{r})=\rho (t_{s},t_{r})-c\delta{t _{j}^{S}}+c\delta{t _{i}^{R}}-Ion*^{f_{2}^{2}}/({f_{1}^{2}}-{f_{2}^{2}})+\delta{Trop_{i}^{j}}+c{N_{1}}_{i}^{j}/f_{1}+\sum \delta _{L1} L1rj(tr)=ρ(ts,tr)−cδtjS+cδtiR−Ion∗f22/(f12−f22)+δTropij+cN1ij/f1+∑δL1
L 2 r j ( t r ) = ρ ( t s , t r ) − c δ t j S + c δ t i R − I o n ∗ f 1 2 / ( f 1 2 − f 2 2 ) + δ T r o p i j + c N 2 i j / f 2 + ∑ δ L 2 {L_{2}}_{r}^{j}(t_{r})=\rho (t_{s},t_{r})-c\delta{t _{j}^{S}}+c\delta{t _{i}^{R}}-Ion*^{f_{1}^{2}}/({f_{1}^{2}}-{f_{2}^{2}})+\delta{Trop_{i}^{j}}+c{N_{2}}_{i}^{j}/f_{2}+\sum \delta _{L2} L2rj(tr)=ρ(ts,tr)−cδtjS+cδtiR−Ion∗f12/(f12−f22)+δTropij+cN2ij/f2+∑δL2
P 1 r j ( t r ) = ρ ( t s , t r ) − c δ t j S + c δ t i R − I o n ∗ f 2 2 / ( f 1 1 − f 2 2 ) + + ∑ δ P 1 {P_{1}}_{r}^{j}(t_{r})=\rho (t_{s},t_{r})-c\delta{t _{j}^{S}}+c\delta{t _{i}^{R}}-Ion*^{f_{2}^{2}}/({f_{1}^{1}}-{f_{2}^{2}})++\sum \delta _{P1} P1rj(tr)=ρ(ts,tr)−cδtjS+cδtiR−Ion∗f22/(f11−f22)++∑δP1
P 2 r j ( t r ) = ρ ( t s , t r ) − c δ t j S + c δ t i R − I o n ∗ f 1 2 / ( f 1 2 − f 2 2 ) + δ T r o p i j + ∑ δ P 2 {P_{2}}_ {r}^ {j}(t_ {r})=\rho (t_ {s},t_ {r})-c\delta {t _{j}^ {S}}+c\delta {t _{i}^ {R}}-Ion*^ {f_{1}^ {2}}/( {f_{1}^ {2}}- {f_{2}^ {2}})+\delta {Trop_{i}^ {j}}+\sum \delta _ {P2} P2rj(tr)=ρ(ts,tr)−cδtjS+cδtiR−Ion∗f12/(f12−f22)+δTropij+∑δP2
4、周跳探测
M-W组合法
L 6 = ( f 1 L 1 − f 2 L 2 ) / ( f 1 − f 2 ) − ( f 1 P 1 − f 2 P 2 ) / ( f 1 + f 2 ) L_{6}=(f_{1}L_{1}-f_{2}L_{2})/(f_{1}-f_{2})-(f_{1}P_{1}-f_{2}P_{2})/(f_{1}+f_{2}) L6=(f1L1−f2L2)/(f1−f2)−(f1P1−f2P2)/(f1+f2)
式中
为MW组合观测值，MW组合消除了卫星与接收机之间的几何距离、对流层延迟、电离层延迟、卫星钟差、和接收机钟差的影响。上式两边同除宽巷模糊度波长
可得：
N w = ( L 1 / λ 1 − L 2 / λ 2 ) − ( f 1 − f 2 ) / ( f 1 + f 2 ) ( P 1 / λ 1 + P 2 / λ 2 ) N_{w}=(L_{1}/\lambda _{1}-L_{2}/\lambda _{2})-(f_{1}-f_{2})/(f_{1}+f_{2})(P_{1}/\lambda _{1}+P_{2}/\lambda_{2} ) Nw=(L1/λ1−L2/λ2)−(f1−f2)/(f1+f2)(P1/λ1+P2/λ2)
为宽巷模糊度。实际应用中，首先用历史数据计算宽巷模糊度的平均值
σ i 2 = ( i − 1 ) / i ∗ σ i − 1 2 + 1 / i ∗ ( N w i − N ˉ w i − 1 ) 2 \sigma _{i}^{2}=(i-1)/i*\sigma _{i-1}^{2}+1/i*(N_{w}^{i}-\bar{N}_{w}^{i-1})^{2} σi2=(i−1)/i∗σi−12+1/i∗(Nwi−Nˉwi−1)2
将当前历元的与历史平均值做差，判断该历元是否发生周跳或者粗差。
参考：《GNSS精密单点定位及非差模糊度快速确定研究方法》李星星
《GNSS数据处理》蒋卫平
LLI标志
LLI（Loss of Lock Indicator）表示失锁标识符，它的范围为0~7，转化为二进制格式000-111，即有3个bit位。其中bit 0和bit 1仅用于相位。
（1）0 或空格：正常或未知
（2）Bit0 置位：先前与当前观测值之间失锁，可能发生了周跳（只针对相位观测值）。
（3）Bit1 置位：接收机进行半周模糊度解算，或程序不能处理半周数据而跳过该观测值的记录（只对当前历元有效）。
（4）Bit2 置位：bit 2置1表示为反欺骗(AS)下的观测值
参考：周跳探测——LLI_lli gnss-CSDN博客
GF(Geometry_free)法
L 1 = ρ + λ 1 N 1 − I 1 L 2 = ρ + λ 2 N 2 − f 1 2 f 2 2 I 1 L g f = L 1 − L 2 = λ 1 N 1 − λ 2 N 2 + f 1 2 − f 2 2 f 2 2 I 1 {L}_{1}=\rho+{\lambda}_{1}{N}_{1}-{I}_{1} \\ {L}_{2}=\rho+{\lambda}_{2}{N}_{2}-\frac{{f}^{2}_{1}}{{f}^{2}_{2}}{I}_{1} \\ {L}_{gf}={L}_{1}-{L}_{2}={\lambda}_{1}{N}_{1}-{\lambda}_{2}{N}_{2}+\frac{{f}^{2}_{1}-{f}^{2}_{2}}{{f}^{2}_{2}}{I}_{1} L1=ρ+λ1N1−I1L2=ρ+λ2N2−f22f12I1Lgf=L1−L2=λ1N1−λ2N2+f22f12−f22I1
通过
∣ L g f 当前历元 − L g f 之前历元 ∣ 是否大于一定阈值来判断发生周跳 |{L}_{gf当前历元}-{L}_{gf之前历元}|是否大于一定阈值来判断发生周跳 ∣Lgf当前历元−Lgf之前历元∣是否大于一定阈值来判断发生周跳
参考：108-周跳探测之GF_周跳检测gf法-CSDN博客
在rtklib的PPP模式中通过后两种方法判断是否发生周跳
二、扩展卡尔曼滤波原理
推荐文章：
卡尔曼滤波系列——（二）扩展卡尔曼滤波-CSDN博客
【精选】扩展卡尔曼滤波_菜鸟知识搬运工的博客-CSDN博客
卡尔曼滤波（Kalman Filter）原理浅析-数学理论推导-2_爱听歌的周童鞋的博客-CSDN博客
扩展卡尔曼滤波相比卡尔曼滤波多了泰勒级数线性化的内容，解算步骤还是一样的。rtklib中用到的就是扩展卡尔曼滤波EKF
状态方程：
观测方程：
进行如下步骤：
1、计算状态转移矩阵
，有的也用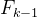
;
状态转移矩阵定义了状态向量随时间变化的规律。
2、计算系统噪声协方差矩阵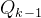
;
该矩阵定义了在卡尔曼滤波模型噪声源的影响下，状态估计的不确定度随时间增长的规律。
3、状态向量先验估计值的传播，从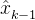
到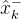
4、误差协方差矩阵的传播(预测)，从
到
;
5、计算观测矩阵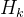
有的也用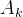
;
6、计算观测噪声协方差矩阵
;
7、计算卡尔曼增益矩阵
;
8、构建观测向量
9、状态向量后验估计值的更新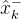到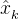
10、误差协方差矩阵的更新（估计），从到
严恭敏老师的《捷联惯导算法与组合导航原理》中也有很详细的公式推导
三、模糊度固定
1、最小二乘模糊度降相关平差法（LAMBDA）
在模糊度固定过程中，对于一个模糊度参数，假设落入其置信区间内的整数个数为n
个，则称这 n 个整数为此模糊度参数的备选解。所有模糊度参数的备选解构成了整个模糊
度向量 N 的备选组，而正确的模糊度组合仅仅是其中的一组。理论上而言，使观测值的
残差平方和最小的一组模糊度即为正确的模糊度组合，即使一个模糊度参数固定错误也会导致较大残差，在解算过程中，每个备选组的残差平方和需耗费巨大工作量。
LAMBDA通过整数变换以减小搜索范围，通过从备选组中挑选模糊度组合使观测值的残差平方和最小等价于：
( N ^ − N ) T Q N ^ − 1 ( N ^ − N ) = m i n 式中， N ^ 为实数模糊度解， N 为所求的模糊度整数解， Q N ^ 为实数模糊度解的协因数阵。 L A M B D A 方法不直接对模糊度参数进行搜索，而是对模糊度实数解 N ^ 及其协因数阵 Q N ^ 进行整数变换： z ^ = Z ^ T ⋅ N ^ Q z ^ = Z T ⋅ Q N ^ ⋅ Z 式中， Z 为整数变换矩阵。整数变换具有以下性质 : 当 N 为整数时，变换后所得 z 也为整数，反之亦然。经过变换之后， z ^ 之间的相关性大幅降低，而且方差也减小，此时式等价于 : ( z ^ − z ) T Q z ^ − 1 ( z ^ − z ) = m i n (\widehat{N}-N)^{T} {Q}^{-1}_{\widehat{N}} (\widehat{N}-N)=min \\ \\ 式中，\widehat{N}为实数模糊度解，N为所求的模糊度整数解，{Q}_{\widehat{N}}为实数模糊度解的协因数阵。\\ LAMBDA方法不直接对模糊度参数进行搜索，而是对模糊度实数解{\widehat{N}}及其协因数阵{Q}_{\widehat{N}}进行整数变换：\\ \\ \widehat{z}={\widehat{Z}}^{T}·\widehat{N} \\ {Q}_{\widehat{z}}=Z^{T}·{Q}_{\widehat{N}}·Z \\ \\ 式中，Z 为整数变换矩阵。整数变换具有以下性质:当 N 为整数时，变换后所得z也为整数，反之亦然。经过变换之后，\\ \widehat{z}之间的相关性大幅降低，而且方差也减小，此时式等价于:\\ \\ (\widehat{z}-z)^{T} {Q}^{-1}_{\widehat{z}} (\widehat{z}-z)=min (N −N)TQN −1(N −N)=min式中，N 为实数模糊度解，N为所求的模糊度整数解，QN 为实数模糊度解的协因数阵。LAMBDA方法不直接对模糊度参数进行搜索，而是对模糊度实数解N 及其协因数阵QN 进行整数变换：z =Z T⋅N Qz =ZT⋅QN ⋅Z式中，Z为整数变换矩阵。整数变换具有以下性质:当N为整数时，变换后所得z也为整数，反之亦然。经过变换之后，z 之间的相关性大幅降低，而且方差也减小，此时式等价于:(z −z)TQz −1(z −z)=min
再利用前面所述算法求得的置信空间，构成值的备选组合，然后逐一搜索挑选出满足上式的整数，值组合。通过前述的整数变换使，值之间的相关性大幅降低，故此时的搜索将相当迅速,求得满足上式的值组合后再实施逆变换:
N = ( Z T ) − 1 ⋅ z N=(Z^{T})^{-1}·z N=(ZT)−1⋅z
N即为所求整周模糊度整数解组合
2、Melbourne-Wuebbena（MW）方法
利用双频P码观测值来确定宽巷模糊度，主要用于LC观测值进行解算时的模糊度固定。
同一历元的相位与双频P码伪距观测值有以下关系：
P 1 = ρ + A f 1 2 P 2 = ρ + A f 2 2 φ 1 = ρ λ 1 + A c f 1 − N 1 φ 2 = ρ λ 2 + A c f 2 − N 2 式中， A 表示电离层影响， ρ 表示接收机至卫星的几何距离以及与频率无关的偏差项， c 表示光速， λ 1 ， f 1 , λ 2 , , f 2 分别表示 L 1 ， L 2 的载波的波长以及频率。由双频 P 码观测值可得： A = f 1 2 f 2 2 f 1 2 − f 2 2 ( P 1 − P 2 ) ρ = f 1 2 f 1 2 − f 2 2 P 1 − f 2 2 f 1 2 − f 2 2 P 2 又有 N 2 − N 1 = φ 1 − φ 2 − f 1 − f 2 f 1 + f 2 ( P 1 λ 1 + P 2 λ 2 ) 上式两端同乘以宽巷观测值的波长 λ w = c f 1 − f 2 , 并令 φ w = φ 1 − φ 2 , N w = N 1 − N 2 , 则有： N w λ w = φ w λ w − f 1 P 1 + f 2 P 2 f 1 + f 2 , 利用该式可表达波长达 86 c m 的宽巷观测值的模糊度参数。 L C 观测值的模糊度参数可以表示为： N c = f 1 2 f 1 2 − f 2 2 N 1 − f 1 f 2 f 1 2 − f 2 2 N 2 对上式进行变换可得 L C 观测值的模糊度参数与相应的宽、窄模糊度参数之间的关系为： N c = 1 λ 1 ( f 1 f 1 + f 2 λ w N w + λ n N n ) 宽巷模糊度 N w 可以通过多个历元的平滑确定，窄巷模糊度 N n 可以通过 L A M B D A 方法确定。回代可求出 L C 观测值的模糊度。 P_{1}=\rho+\frac{A}{f^{2}_{1}} \\ P_{2}=\rho+\frac{A}{f^{2}_{2}} \\ \varphi_{1}=\frac{\rho}{\lambda_{1}}+\frac{A}{cf_{1}}-N_{1} \\ \varphi_{2}=\frac{\rho}{\lambda_{2}}+\frac{A}{cf_{2}}-N_{2} \\ 式中，A表示电离层影响，\rho 表示接收机至卫星的几何距离以及与频率无关的偏差项，c表示光速，\\ \lambda_{1}，f_{1},\lambda_{2},,f_{2}分别表示L1，L2的载波的波长以及频率。由双频P码观测值可得： \\ A=\frac{f^{2}_{1} f^{2}_{2}}{f^{2}_{1}-f^{2}_{2}}(P_{1}-P_{2}) \\ \rho=\frac{f^{2}_{1}}{f^{2}_{1}-f^{2}_{2}}P_{1}-\frac{f^{2}_{2}}{f^{2}_{1}-f^{2}_{2}}P_{2} \\ 又有N_{2}-N_{1}=\varphi_{1}-\varphi_{2}-\frac{f_{1}-f_{2}}{f_{1}+f_{2}}(\frac{P_{1}}{\lambda_{1}}+\frac{P_{2}}{\lambda_{2}}) \\ 上式两端同乘以宽巷观测值的波长\lambda_{w}=\frac{c}{f_{1}-f_{2}},并令\varphi_{w}=\varphi_{1}-\varphi_{2},N_{w}=N_{1}-N_{2},则有： \\ N_{w}\lambda_{w}=\varphi_{w} \lambda{w}-\frac{f_{1}P_{1}+f_{2}P_{2}}{f_{1}+f_{2}},利用该式可表达波长达86cm的宽巷观测值的模糊度参数。 \\ LC观测值的模糊度参数可以表示为：N_{c}=\frac{f^{2}_{1}}{f^{2}_{1}-f^{2}_{2}}N_{1}-\frac{f_{1}f_{2}}{f^{2}_{1}-f^{2}_{2}}N_{2} \\ 对上式进行变换可得LC观测值的模糊度参数与相应的宽、窄模糊度参数之间的关系为：\\ N_{c}=\frac{1}{\lambda_{1}}(\frac{f_{1}}{f_{1}+f_{2}}\lambda_{w}N_{w}+\lambda_{n}N_{n}) \\ 宽巷模糊度N_{w}可以通过多个历元的平滑确定，窄巷模糊度N_{n}可以通过LAMBDA方法确定。回代可求出LC观测值的模糊度。 P1=ρ+f12AP2=ρ+f22Aφ1=λ1ρ+cf1A−N1φ2=λ2ρ+cf2A−N2式中，A表示电离层影响，ρ表示接收机至卫星的几何距离以及与频率无关的偏差项，c表示光速，λ1，f1,λ2,,f2分别表示L1，L2的载波的波长以及频率。由双频P码观测值可得：A=f12−f22f12f22(P1−P2)ρ=f12−f22f12P1−f12−f22f22P2又有N2−N1=φ1−φ2−f1+f2f1−f2(λ1P1+λ2P2)上式两端同乘以宽巷观测值的波长λw=f1−f2c,并令φw=φ1−φ2,Nw=N1−N2,则有：Nwλw=φwλw−f1+f2f1P1+f2P2,利用该式可表达波长达86cm的宽巷观测值的模糊度参数。LC观测值的模糊度参数可以表示为：Nc=f12−f22f12N1−f12−f22f1f2N2对上式进行变换可得LC观测值的模糊度参数与相应的宽、窄模糊度参数之间的关系为：Nc=λ11(f1+f2f1λwNw+λnNn)宽巷模糊度Nw可以通过多个历元的平滑确定，窄巷模糊度Nn可以通过LAMBDA方法确定。回代可求出LC观测值的模糊度。
在rtklib中pppamb 中
if (n<=0||rtk->opt.ionoopt!=IONOOPT_IFLC||rtk->opt.nf<2) return 0;
只有消电离层模型可以进行模糊度固定。
参考《GNSS数据处理》
四、各项误差改正
1、与卫星有关的误差
卫星天线相位中心偏差改正
GNSS观测量是相对于卫星天线相位中心的，而卫星定轨所用的轨道力模型参数、IGS精密星历和卫星钟差是相对于卫星质量中心，因此建立观测方程时必须顾及卫星天线质量中心和相位中心之间的偏差（《GNSS数据处理》蒋卫平）。卫星天线相位中心偏差包括两个部分，一个是基于物理参考位置的平均相位中心偏移（ＰＣＯ），另一个是相位中心变化值，与高度角和方位角有关，是一个变化量。RTKLIB中采用的是绝对相位中心修正模型（ＩＧＳ－０８）[1]。表示为：
Δ φ ( a , z ) = Δ φ t ( a , z ) + Δ r × e 式中： Δ r 为天线参考点到平均相位中心的几何矩阵； e 为接收机到卫星端方向上的旋转矩阵； a 为卫星的方位角； z 表示接收机的天顶角； Δ φ t ( a , z ) 表示天线相位中心的变化改正值； Δ φ ( a , z ) 表示方位角与天顶角总的相位中心改正量。 \Delta\varphi(a,z)=\Delta\varphi^{t}(a,z)+\Delta \pmb{r} \times \pmb{e} \\ 式中：\Delta\pmb{r}为天线参考点到平均相位中心的几何矩阵；\pmb{e}为接收机到卫星端方向上的旋转矩阵；a为卫星的方位角；z表示接收机的天顶角；\\ \Delta\varphi^{t}(a,z)表示天线相位中心的变化改正值；\Delta\varphi(a,z)表示方位角与天顶角总的相位中心改正量。 Δφ(a,z)=Δφt(a,z)+Δr×e式中：Δr为天线参考点到平均相位中心的几何矩阵；e为接收机到卫星端方向上的旋转矩阵；a为卫星的方位角；z表示接收机的天顶角；Δφt(a,z)表示天线相位中心的变化改正值；Δφ(a,z)表示方位角与天顶角总的相位中心改正量。
相位缠绕改正
GNSS卫星发射的是右旋极化（RHCP）的电磁波信号，接收机观测到的相位值依赖于卫星与接收机天线间的方位关系。接收机天线或卫星天线绕极化轴方向的旋转会改变相位观测值，最大可达一周(天线旋转一周)，这个效应就称为“相位缠绕”。对于接收机天线而言，如果是静态观测，天线不发生旋转。但是对于卫星天线，卫星为了保持其太阳能翼板指向太阳，卫星天线相应地会发生缓慢的旋转，而且站星间的几何关系也不断变化。此外在卫星进出地影区域时，卫星为了使其太阳能翼板指向太阳会快速旋转。卫星在0.5h 内可旋转一周，在这段时间，载波相位观测数据需要进行相位缠绕改正，或者删除该部分数据（《GNSS数据处理》蒋卫平）。相位缠绕修正公式为[1]
Δ ϕ = s i g n ( ξ ) a r c c o s ( D t ⋅ D ∣ D t ∣ ∣ D ∣ ) 式中： ξ = k ⋅ ( D t × D ) ； k 为卫星到接收机单位向量； D t 和、 D 分别为卫星到接收机天线的有效偶极矢量， D t = x t − k ( k ⋅ x t ⋅ y t ) D = x − k ( k ⋅ x ) + k ⋅ y t \Delta \phi=sign(\xi)arccos(\frac{\pmb{D}^{t}\pmb{·D}}{|\pmb{D}^{t}||\pmb{D}|})\\ 式中：\xi=\pmb{k·}(\pmb{D}^{t}\times \pmb{D})；\pmb{k}为卫星到接收机单位向量；\pmb{D}^{t}和、\pmb{D}分别为卫星到接收机天线的有效偶极矢量，\\ \pmb{D}^{t}=\pmb{x}^{t}-\pmb{k}(\pmb{k·x}^{t}\pmb{·y}^{t})\\ \pmb{D}=\pmb{x}-\pmb{k}(\pmb{k·x})+\pmb{k·y}^{t} Δϕ=sign(ξ)arccos(∣Dt∣∣D∣Dt⋅D)式中：ξ=k⋅(Dt×D)；k为卫星到接收机单位向量；Dt和、D分别为卫星到接收机天线的有效偶极矢量，Dt=xt−k(k⋅xt⋅yt)D=x−k(k⋅x)+k⋅yt
2、与传播路径有关的误差
电离层延迟
Ionosphere-free LC
在消电离层模型中通过双频观测值的组合来消除或减弱电离层影响，详细PPP基础方程。
Single layer model
在RTKLIB的manual找到如下：
对流层延迟
对流层延迟一般泛指非电离大气对电磁波信号的折射。非电离大气包括对流层和平流层，大约是大气层中从地表面向上 50km 的部分。由于折射的 80% 发生在对流层，所以通常将两者对 GPS 信号的影响统称为对流层延迟。研究表明，对于工作频率在15GH 以内的微波而言，对流层使该种信号的传播路径比几何路径长，所导致的传播路径弯曲较小可忽略不计。对流层导致的 GNSS 信号传播路径增长的距离即为对流层延迟量，天顶方向的对流层延迟约为 2.3m;当卫星高度角为 10时，对流层延迟将增加至 13m 左右。（《GNSS数据处理》）
对流层延迟通常包括干延迟量和湿延迟量，90%左右是干分量，10%左右是湿分量；干分量可以通过 Saastamoinen先验 模型精确修正，湿分量是由大气中的水汽引起的，变化较快，难以通过模型完全修正，对流层延迟采用RTKLIB中的水平梯度的对流层改正模型[1]
Δ T = m ( ε ) h ⋅ Z H D + m ( ε ) w ⋅ Z W D + m ( ε ) a z i ⋅ ( G N c o s φ + G E s i n φ ) 式中， Z H D 为天顶干延迟； Z W D 为天顶湿延迟； m ( ⋅ ) 为映射函数； ε 为高度角；下标 h 和 w 各自为干延迟和湿延迟； z a i 为梯度； φ 为方位角， ( G N c o s φ + G E s i n φ ) 为梯度向量 ( G N , G E ) 和方位角 ( c o s φ , s i n φ ) 的点积； m ( ε ) a z i = m ( ε ) w t a n ε \Delta T=m(\varepsilon)_{h}\pmb{·}ZHD+m(\varepsilon)_{w}\pmb{·}ZWD+m(\varepsilon)_{azi}\pmb{·}(G_{N}cos\varphi+G_{E}sin\varphi) \\ 式中，ZHD为天顶干延迟；ZWD为天顶湿延迟；m(·)为映射函数；\varepsilon为高度角；下标h和w各自为干延迟和湿延迟；zai为梯度；\\ \varphi为方位角，(G_{N}cos\varphi+G_{E}sin\varphi)为梯度向量(G_{N},G_{E})和方位角(cos\varphi,sin\varphi)的点积；m(\varepsilon)_{azi}=\frac{m(\varepsilon)_{w}}{tan\varepsilon} ΔT=m(ε)h⋅ZHD+m(ε)w⋅ZWD+m(ε)azi⋅(GNcosφ+GEsinφ)式中，ZHD为天顶干延迟；ZWD为天顶湿延迟；m(⋅)为映射函数；ε为高度角；下标h和w各自为干延迟和湿延迟；zai为梯度；φ为方位角，(GNcosφ+GEsinφ)为梯度向量(GN,GE)和方位角(cosφ,sinφ)的点积；m(ε)azi=tanεm(ε)w
在RTKLIB的manual中基础对流层计算模型（ Saastamoinen）：
p = 1013.25 × ( 1 − 2.2557 × 1 0 − 5 h ) 5.2568 T = 15.0 − 6.5 × 1 0 − 3 h + 273.15 e = 6.108 × e x p { 17.15 T − 4684.0 T − 38.45 } × h r e l 100 p 为总压强 ( h P a ) , T 是空气绝对温度 ( K ) ， h 为海拔高， e 是水蒸气分压， h r e l 是相对湿度 则对流层延迟 T r s = 0.002277 c o s z { p + ( 1255 T + 0.05 ) e − t a n 2 z } 上式中， z 是天顶角 ( 弧度 ) ， z = π / 2 − E l r s p=1013.25\times(1-2.2557 \times 10^{-5}h)^{5.2568} \\ T=15.0-6.5 \times10^{-3}h+273.15 \\ e=6.108 \times exp\{\frac{17.15T-4684.0}{T-38.45}\} \times \frac{h_{rel}}{100} \\ \\ p为总压强(hPa),T是空气绝对温度(K)，h为海拔高，e是水蒸气分压，h_{rel}是相对湿度 \\ \\ 则对流层延迟T^{s}_{r}=\frac{0.002277}{cosz}\{ p+(\frac{1255}{T}+0.05)e-tan^{2}z \} \\ 上式中，z是天顶角(弧度)，z=\pi /2-El^{s}_{r} p=1013.25×(1−2.2557×10−5h)5.2568T=15.0−6.5×10−3h+273.15e=6.108×exp{T−38.4517.15T−4684.0}×100hrelp为总压强(hPa),T是空气绝对温度(K)，h为海拔高，e是水蒸气分压，hrel是相对湿度则对流层延迟Trs=cosz0.002277{p+(T1255+0.05)e−tan2z}上式中，z是天顶角(弧度)，z=π/2−Elrs
精密对流层模型
当"Troposphere Correction"为"Estimate ZTD"或"Estimate ZTD+Grad"，使用如下精密模型
m ( E l r s ) Z H , r + m ( E l r s ) ( Z T , r − Z H , r ) T r s = m H ( E l r s ) Z H , r + m ( E l s r ) ( Z T , r − Z H , r ) 其中： Z T , r : 对流层天顶总延迟 Z H , r : t r o p o s p h e r i c z e n i t h h y d r o − s t a t i c d e l a y 通过 S a a s t a m o i n e n 模型获取，即上式的 T r s 当 z = 0 , h r e l = 0 时 m H ( E l ) : h y d r o − s t a t i c m a p p i n g f u n c t i o n m w ( E l ) : w e t m a p p i n g f u n c t i o n R T K L I B 默认应用 N M F ( N i e l l m a p p i n g f u n c t i o n ) Z T , r 作为未知参数被估计，在 " E s t i m a t e Z T D + G r a d " 模式中， G N , r , G H , r 也被视作未知参数 m(El^{s}_{r})Z_{H,r}+m(El^{s}_{r})(Z_{T,r}-Z_{H,r}) \\ T^{s}_{r}=m_{H}(El^{s}_{r})Z_{H,r}+m(El^{s}{r})(Z_{T,r}-Z_{H,r}) \\ 其中：Z_{T,r}:对流层天顶总延迟 \\ Z_{H,r}:tropospheric zenith hydro-static delay通过Saastamoinen模型获取，即上式的T^{s}_{r}当z=0,h_{rel}=0时 \\ m_{H}(El):hydro-static mapping function \\ m_{w}(El):wet mapping function \\ RTKLIB默认应用NMF(Niell \ mapping \ function) \\ Z_{T,r}作为未知参数被估计，在"Estimate ZTD+Grad"模式中，G_{N,r},G_{H,r}也被视作未知参数 m(Elrs)ZH,r+m(Elrs)(ZT,r−ZH,r)Trs=mH(Elrs)ZH,r+m(Elsr)(ZT,r−ZH,r)其中：ZT,r:对流层天顶总延迟ZH,r:troposphericzenithhydro−staticdelay通过Saastamoinen模型获取，即上式的Trs当z=0,hrel=0时mH(El):hydro−staticmappingfunctionmw(El):wetmappingfunctionRTKLIB默认应用NMF(Niell mapping function)ZT,r作为未知参数被估计，在"EstimateZTD+Grad"模式中，GN,r,GH,r也被视作未知参数
3、与接收机测站有关的误差
固体潮改正
摄动天体 (月亮、太阳) 对弹性地球的引力作用，使地球表面产生周期性的涨落称为地球固体潮现象。它使地球在地心与摄动天体的连线方向拉长，与连线垂线方向上趋于扁平。固体潮对测站的影响包含着与纬度有关的长期偏移和主要由半日周期组成的周期项（《GNSS数据处理》）。
测站固体潮改正的近似公式为[1]
Δ r = ∑ j − 2 3 G M j G M ⋅ r 4 ∣ R J 3 ∣ { 3 l 2 × X P ⋅ X j ∣ X P ∣ ∣ X j ∣ × X j ∣ X j ∣ + [ 3 ( h 2 2 − l 2 ) × [ X P ⋅ X j ∣ X P ∣ ∣ X j ∣ ] 2 z − h 2 2 × X j ∣ X j ∣ ] × X P ∣ X P ∣ } + [ − 0.025 s i n φ c o s φ s i n ( θ + λ ) ] × X P ∣ X P ∣ 式中： G M 为地心引力常数； r 为测站到地心的距离； G M J 为引力常数， j = 2 表示月球引力常数， j = 3 为日心引力常数； X j 为天体在地心参考框架的坐标向量； Ｘ P 为在地心参考框架中测站坐标向量； θ 为格林尼治平恒星时； h 2 为 0.6090 ； l 2 为 0.0852 ； λ 和 φ 分别为测站纬度与经度 \Delta \pmb{r}=\sum\nolimits^{3}_{j-2} \frac{GM_{j}}{GM} \pmb{·} \frac{r^{4}}{|\pmb{R}^{3}_{J}|} \{3l_{2}\times \frac{\pmb{X}_{P}\pmb{·X}_{j}}{|\pmb{X}_{P}||\pmb{X}_{j}|} \times \frac{\pmb{X}_{j}}{|\pmb{X}_{j}|} +[3(\frac{h_{2}}{2}-l_{2}) \times [\frac{\pmb{X}_{P}\pmb{·X}_{j}}{|\pmb{X}_{P}||\pmb{X}_{j}|}]^{2}z-\frac{h_{2}}{2} \times \frac{\pmb{X}_{j}}{|\pmb{X}_{j}|}]\times \frac{\pmb{X}_{P}}{|\pmb{X}_{P}|} \}\\ +[-0.025sin\varphi cos\varphi sin(\theta+\lambda)]\times \frac{\pmb{X}_{P}}{|\pmb{X}_{P}|}\\ \\ 式中：GM为地心引力常数；r为测站到地心的距离；GMJ为引力常数，j=2表示月球引力常数，j=3为日心引力常数；\\ X_{j}为天体在地心参考框架的坐标向量；Ｘ_{P} 为在地心参考框架中测站坐标向量；θ为格林尼治平恒星时；h_{2}为0.6090；\\ l_{2}为0.0852；λ和\varphi分别为测站纬度与经度 Δr=∑j−23GMGMj⋅∣RJ3∣r4{3l2×∣XP∣∣Xj∣XP⋅Xj×∣Xj∣Xj+[3(2h2−l2)×[∣XP∣∣Xj∣XP⋅Xj]2z−2h2×∣Xj∣Xj]×∣XP∣XP}+[−0.025sinφcosφsin(θ+λ)]×∣XP∣XP式中：GM为地心引力常数；r为测站到地心的距离；GMJ为引力常数，j=2表示月球引力常数，j=3为日心引力常数；Xj为天体在地心参考框架的坐标向量；ＸP为在地心参考框架中测站坐标向量；θ为格林尼治平恒星时；h2为0.6090；l2为0.0852；λ和φ分别为测站纬度与经度
大洋潮汐改正
由于日月引力作用，实际的海平面相对于平均海平面会有周期性的潮汐变化，即海潮。地壳对海潮的这种海水质量重新分布所产生的弹性效应通常称为海潮负载。它引起的台站位移要比固体潮的影响小一个量级，约为几厘米，但规律性要差一些（《GNSS数据处理》）。改正模型[1]：
Δ c = ∑ j f j A c j c o s ( ω j t + χ j + u j + φ c j ) 式中： Δ c 为对测站坐标分量影响； f j 为 j 的分量比例因子； A c j 为潮汐 j 分量对坐标的影响幅度； ω j 为 j 分量的相位角偏差； φ c j 为潮汐 j 分量对坐标影响的相位角，其中 j = 1 , 2 , 3 ⋅ ⋅ ⋅ 11 \Delta c=\sum\nolimits_{j}f_{j}A_{cj}cos(\omega_{j}t+\chi{j}+u_{j}+\varphi_{cj}) \\ \\ 式中：\Delta c为对测站坐标分量影响；f_{j}为j的分量比例因子；A_{cj}为潮汐j分量对坐标的影响幅度；\\ \omega_{j}为j分量的相位角偏差；\varphi_{cj}为潮汐j分量对坐标影响的相位角，其中j=1,2,3···11 Δc=∑jfjAcjcos(ωjt+χj+uj+φcj)式中：Δc为对测站坐标分量影响；fj为j的分量比例因子；Acj为潮汐j分量对坐标的影响幅度；ωj为j分量的相位角偏差；φcj为潮汐j分量对坐标影响的相位角，其中j=1,2,3⋅⋅⋅11
地球极潮改正
由于极移现象的存在，地球自转产生的离心力可使得地球发生形变，称为极潮。极移使地球自转轴在北极描出直径约 20cm 的圆，极潮位移取决于观测瞬间自转轴与地壳的交点位置，它随时间而变化。极潮引起的台站漂移为1~2cm（GNSS数据处理）。
RTKLIB中的地球潮汐模型是根据 IERS Conventions 2010 solid earth tides model
4、其他误差
地球自转校正[2]
参考文献：
[1]潘军道,韦照川,杨柯.基于RTKLIB的精密单点定位及结果分析[J].Gnss World OF China,2017,42(1):95-99
[2]杨旭.GNSS多系统融合短基线解算方法研究与软件实现[D].安徽:安徽理工大学，2016：1-101
五、代码分析
在RTKLIB架构下的详细代码分析 可以前往：
RTKLIB学习（二）–2、PPP代码分析-CSDN博客