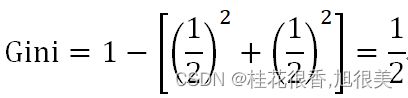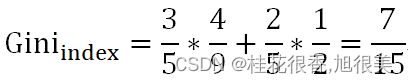GBDT（梯度提升树 Gradient Boosting Decison Tree）学习笔记

介绍

集成学习Boosting一族将多个弱学习器(或称基学习器)提升为强学习器，像AdaBoost, GBDT等都属于“加性模型”(Additive Model)，即基学习器的线性组合。

• AdaBoost： 先从初始训练集训练出一个基学习器，然后基于基学习器的在这一轮的表现，在下一轮训练中给预测错的训练样本更大权重值，以达到逐步减少在训练集的预测错误率。
• GBDT： 先产生一个弱学习器(CART回归树模型)，训练后得到输入样本的残差，然后再产生一个弱学习器，基于上一轮残差进行训练。不断迭代，最后加权结合所有弱学习器得到强学习器。

GBDT的一个应用示意图如下（某样本预测值 = 它在不同弱学习器所在叶子节点输出值的累加值）：

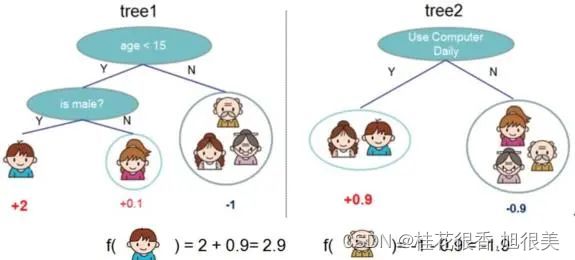
GBDT可用于回归和分类任务。

GBDT弱学习器

决策树是IF-THEN结构，它学习的关键在于如何选择最优划分属性。随着划分过程不断进行，希望决策树的分支结点所包含的样本尽可能属于同一类别，即结点的“纯度”(Purity)越来越高”。衡量纯度的指标有多种，因此对应有不同类型的决策树算法，例如ID3决策树 (以信息增益Information Gain作为属性划分标准)，C4.5决策树 (以增益率Gain Ratio选择最优划分属性)，CART决策树 (使用基尼指数Gini Index)来选择划分属性。

决策树那么多种，为什么GBDT的弱学习器就限定使用CART决策树？

• ID3决策树只支持类别型变量，而C4.5和CART支持连续型和类别型变量。
• C4.5适用于小样本，CART适用于大样本。

CART决策树怎么计算基尼值？

假设当前数据集D中第k类样本所占比例为Pk (k=1,2,…,|y|)，则基尼值为：

Gini( D ) 反映了从数据集D随机抽取两个样本，其类别标记不一致的概念，因此越小，数据集D的纯度越高。基于此，属性a的基尼指数定义为：

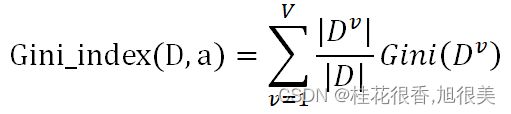
假设属性a有V个可能的取值{}，则Dv是指第v个分支结点包含D中所有在属性a上取值为av的样本。|Dv|/|D|是给分支结点赋予权重，获得样本数更多的结点，影响更大。

计算基尼指数的例子

假如按照“芯片为高通骁龙865和非高通骁龙865进行机型档位划分”：

当芯片为高通骁龙865时，有旗舰机2个，中端机1个：

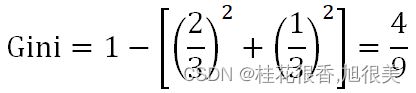
当芯片非高通骁龙865时，有中端机1个，低端机1个：

最后，特征”芯片”下数据集的基尼指数是：

为什么GBDT用回归树，不用分类树？

因为GBDT要计算残差，且预测结果是通过累加所有树结果得到的。因此分类树没法产生连续型结果满足GBDT的需求。
GBDT算法实现流程图及伪代码:

负梯度和残差的关系是什么？

负梯度是函数下降最快的方向，也是GBDT目标函数下降最快的方向，所以，我们用负梯度去拟合模型。而残差只是一个负梯度的特例，当损失函数为均方损失时，负梯度刚好是残差。

GBDT回归

（1）GBDT二分类

GBDT本质上就是一系列弱学习器之和：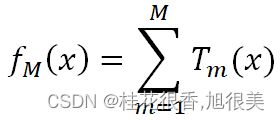
而GBDT分类跟逻辑回归的思路是类似的，将的作为下列函数的输入，便可以得到类别概率值：
假设样本独立且同分布，极大似然估计(即选取合适的参数使被选取的样本在总体中出现的可能性最大)的损失函数为：
为了方便对损失函数求导，会加入对数，求最大对数似然估计：

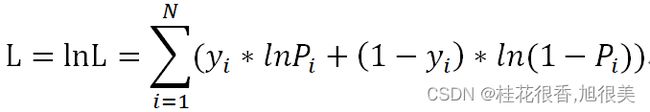
上面的损失函数并非最终的函数，而是最大似然估计函数（数值越大越好），由于损失函数应该使越小越好，所以要对上面的L取相反数，同时为了得到平均到每个样本的损失值，要除以样本数N，这样得到了最终的损失函数：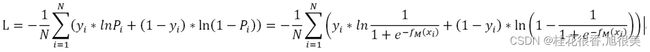
对损失函数计算负梯度：

由此看来，GBDT负梯度即为残差，表示真实概率和预测概率的差值。接下来计算过程跟着GBDT通用框架进行就好了。

（2）GBDT多分类

GBDT多分类原理跟Softmax一样的，假设我们有k个类别，将作为以下函数的输入，便可以类别q对应的概率值：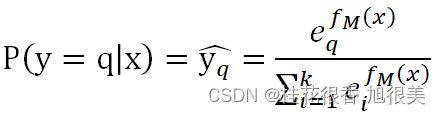
其损失函数为：

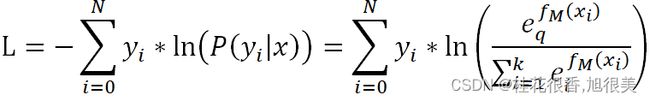
多类别任务下，只有一个类别是1，其余为0，假设这不为0的一类为q，我们对它Softmax的损失函数求负梯度得：

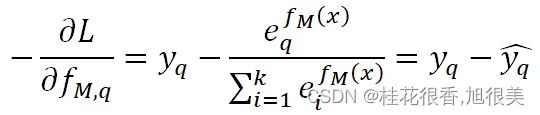
跟二分类一样，本质上负梯度就是真实概率和预测概率的插值。

正则化

（1）学习率v和树数量M的平衡

第m轮下的强学习器 = 第m-1轮下的强学习器 + 第m轮的弱学习器，如下：

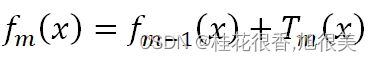
GBDT原论文提到，树数量越多，越容易过拟合，所以限制树数量可以避免过拟合，但历史研究又给出：通过收缩 (即学习率v减少) 实现的正则化比通过限制项 (即树数量M减少) 实现的正则化效果更好。

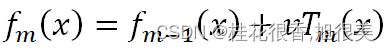
该公式加入了学习率v，这里跟神经网络的学习率相反，如果我们学习率下降，每个树的贡献就会减低，反而还实现了正则化，但如果我们放开训练(即不固定树数量)，只减低学习率的话，GBDT还是会过拟合，因为产生了更多的树。因此，GBDT作者建议，我们要实现v-M之间的权衡，理想的应该是在正则效果合适下，学习率降低的同时，也能尽可能保证树数量少些。这里当然也有出于对计算资源的考虑，增加M会带来计算开销。

（2）子采样比例

子采样是将原数据集中抽样一定的样本去拟合GBDT。与随机森林不同的是，GBDT采样不放回抽样，因为GBDT串行训练要求所有弱学习器使用同一套样本集，不然在不同抽样样本空间计算的残差，缺乏一致性。

（3）决策树常用正则化手段

这块的参数都涉及到弱学习器树本身的正则化，例如：决策树最大深度、划分所需最少样本数、叶子节点最少样本数、叶子节点最小样本权重、最大叶子节点数、节点划分最小不纯度等。

优缺点

优点：

• 采用基于“残差”(严格来说是负梯度)的Boosting集成手段。
• 适用于回归、二分类和多分类任务。
• 预测精度比RF高。
• 对异常值的鲁棒性强（采用了Huber损失和分位数损失）。

缺点：

• 串行方式的模型训练，难并行，造成计算开销。
• 不适合高维稀疏离散特征。这是决策树的痛点，比如动物类别采用one-hot编码后，会产生是否为狗，是否为猫一系列特征，而若这一系列特征中大量样本为狗，其它动物很少，那么树在划分属性时，很容易就划分为“是否为狗”，从而产生过拟合，它不像LR等线性模型f(w,x)的正则化权重是对样本惩罚（可以实现对狗样本给与更大的惩罚项），而树的惩罚项往往是树结构相关的，因此样本层面的惩罚较小，使得在高维稀疏特征时，GBDT表现不好。

与RF的对比

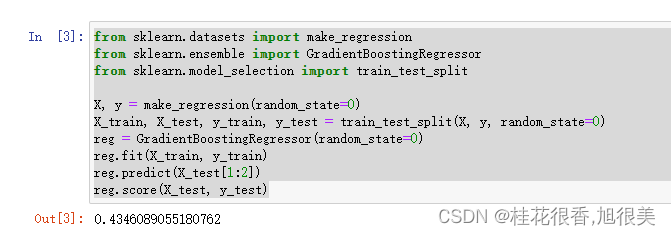
代码参考

from sklearn.datasets import make_regression
from sklearn.ensemble import GradientBoostingRegressor
from sklearn.model_selection import train_test_split

X, y = make_regression(random_state=0)
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=0)
reg = GradientBoostingRegressor(random_state=0)
reg.fit(X_train, y_train)
reg.predict(X_test[1:2])
reg.score(X_test, y_test)

运行结果：