双极性信号、QPSK、4-PAM在AWGN信道下传输的MATLAB仿真
分享三个程序:
1. 双极性信号通过AWGN信道后的误比特率性能
仿真程序
% 基带双极性信号通过AWGN信道
clear all
clc
close
nsamp=10; %每个脉冲信号的抽样点数
s0=ones(1,nsamp); %基带脉冲信号
s1=-s0;
nsymbol=500000; %每种信噪比下的发送符号数
EbN0=0:10; %信噪比,E/N0
msg=randi([0, 1], 1, nsymbol); %消息数据
s00=zeros(nsymbol,1);
s11=zeros(nsymbol,1);
indx=find(msg==0); %比特0在发送消息中的位置
s00(indx)=1;
s00=s00*s0; %比特0影射为发送波形s0
indx1=find(msg==1); %比特1在发送消息中的位置
s11(indx1)=1;
s11=s11*s1; %比特1映射为发送波形s1
s=s00+s11; %总的发送波形
s=s'; %数据转置,方便接收端处理
for indx=1:length(EbN0)
decmsg=zeros(1,nsymbol);
r=awgn(s,EbN0(indx)-7); %通过AWGN信道
r00=s0*r; %与s0相关
indx1=find(r00<0);
decmsg(indx1)=1; %判决
[err,ber(indx)]=biterr(msg,decmsg);
end
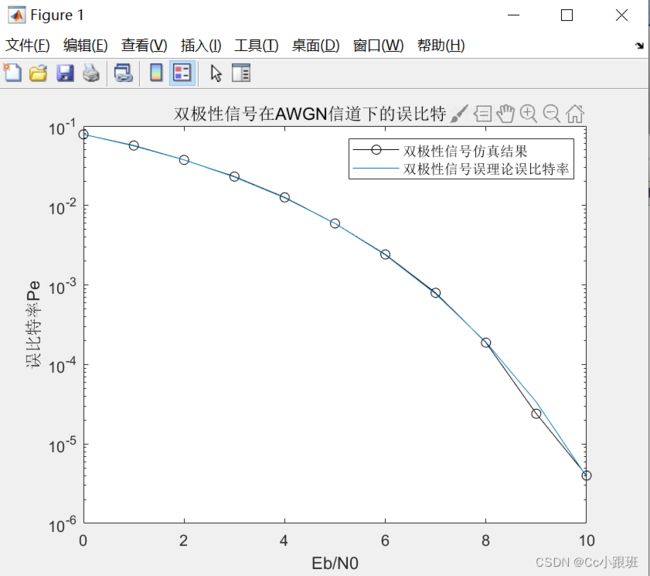
semilogy(EbN0,ber,'-ko',EbN0,qfunc(sqrt(2*10.^(EbN0/10))));
title('双极性信号在AWGN信道下的误比特率性能')
xlabel('Eb/N0');ylabel('误比特率Pe')
legend('双极性信号仿真结果','双极性信号误理论误比特率')
仿真结果
增加符号数会使曲线更平滑,和理论误比特率更吻合。
2. QPSK载波调制在AWGN信道下传输的误符号率性能
仿真程序
clear all;clc;close all;
type=2;
nsymbol=100000; %每种信噪比下的发送符号数
T=1; %符号周期
fs=100; %每个符号的采样点数
ts=1/fs; %采样时间间隔
t=0:ts:T-ts; %时间向量
fc=10; %载波频率
c=exp(j*2*pi*fc*t); %载波信号
c1=cos(2*pi*fc*t); %同相载波
c2=-sin(2*pi*fc*t); %正交载波
M=4; %QPSK
EsN0=0:15; %信噪比,Es/N0
snr1=10.^(EsN0/10); %信噪比转换为线性值
%% pskmod
if type == 1
msg1=randi([0, 1], 1, nsymbol); %消息数据
msg = 1 - 2 * msg1; % 进行符号映射,得到双极性信号
% 串并转换
% 生成I路信号
x_i = msg(1 : 2: end);
% 生成Q路信号
x_q = msg(2 : 2: end);
msgmod = (x_i+1i*x_q).';
end
if type == 2
msg1=randi([0, 3], 1, nsymbol); %消息数据
msgmod=pskmod(msg1,M,pi/4).';
end
%%
size(msgmod);
size(c);
tx=real(msgmod*c); %载波调制
tx1=reshape(tx.',1,length(msgmod)*length(c));
spow=norm(tx1).^2/nsymbol; %求每个符号的平均功率
for indx=1:length(EsN0)
sigma=sqrt(spow/(2*snr1(indx))); %根据符号功率求噪声功率
rx=tx1+sigma*randn(1,length(tx1)); %加入高斯白噪声
rx1=reshape(rx,length(c),length(msgmod));
r1=(c1*rx1)/length(c1); %相关运算
r2=(c2*rx1)/length(c2);
%% 判决
if type == 1
% 对I路信号进行判决
for m = 1 : length(r1)
if r1(m) >= 0
r1(m) = 1;
else
r1(m) = -1;
end
end
% 对Q路信号进行判决
for n = 1 : length(r2)
if r2(n) >= 0
r2(n) = 1;
else
r2(n) = -1;
end
end
% 并串转换
rx_data = zeros(1, 2 * length(r1));
rx_data(1, 1: 2: end) = r1;
rx_data(1, 2 : 2: end) = r2;
y = (1-rx_data)/2; % 符号逆映射 1--0 -1--1
end
if type == 2
r=r1+j*r2;
y=pskdemod(r,M,pi/4); %PSK解调
end
[err,ser(indx)]=symerr(msg1,y); %误符号率
end
ser1=2*qfunc(sqrt(2*snr1)*sin(pi/M)); %理论误符号率
semilogy(EsN0,ser,'-k*',EsN0,ser1);
title('QPSK载波调制信号在AWGN信道下的性能')
xlabel('Es/N0');ylabel('误符号率')
legend('误符号率','理论误符号率')
仿真结果
3. 4-PAM调制信号通过带限信道传输
调制信号在发送端和接收端分别采用滚降系数为0.25,时延为5的根升余弦滤波器进行谱成形,
仿真程序
clear all
nsymbol=100000; %每种信噪比下的发送符号数
Fd=1; %符号采样频率
Fs=10; %滤波器采样频率
rolloff=0.25; %滤波器滚降系数
delay=5; %滤波器时延
M=4; %4-PAM
graycode=[0 1 3 2]; %Gray编码规则
EsN0=0:15; %信噪比,E/N0
msg=randi([0, 3], 1, nsymbol); %消息数据
% msg=randint(1,nsymbol,4); %消息数据
msg1=graycode(msg+1); %Gray映射
msgmod=pammod(msg1,M); %4-PAM调制
rrcfilter = rcosine(Fd,Fs,'fir/sqrt',rolloff,delay); %设计根升余弦滤波器
s=rcosflt(msgmod,Fd,Fs,'filter',rrcfilter);
for indx=1:length(EsN0)
decmsg=zeros(1,nsymbol);
r=awgn(real(s),EsN0(indx)-7,'measured');
rx=rcosflt(r,Fd,Fs,'Fs/filter',rrcfilter);
rx1=downsample(rx,Fs);
rx2=rx1(2*delay+1:end-2*delay);
msg_demod=pamdemod(rx2,M); %%判决
decmsg=graycode(msg_demod+1); %Gray逆映射
[err,ber(indx)]=biterr(msg,decmsg,log2(M)); %求误比特率
[err,ser(indx)]=symerr(msg,decmsg);
end
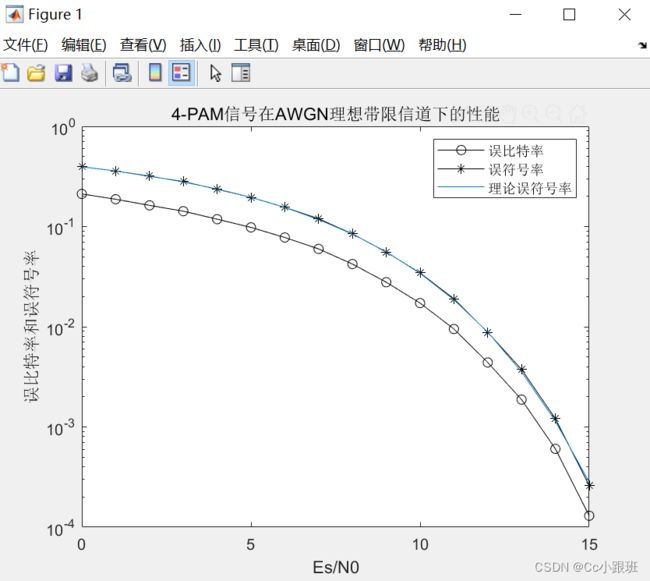
semilogy(EsN0,ber,'-ko',EsN0,ser,'-k*',EsN0,1.5*qfunc(sqrt(0.4*10.^(EsN0/10))));
title('4-PAM信号在AWGN理想带限信道下的性能')
xlabel('Es/N0');ylabel('误比特率和误符号率')
legend('误比特率','误符号率','理论误符号率')
仿真结果
程序参考自书本:详解MATLAB/SIMULINK 通信系统建模与仿真 (百度网盘分享链接,提取码:3333)