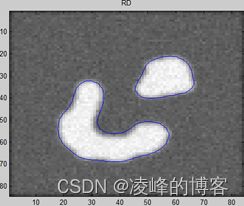
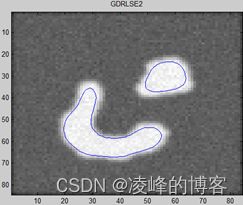
基于 Level set 方法的医学图像分割
摘 要
医学图像分割是计算机辅助诊断系统设计中的关键技术。对于医学图像分割问题,它一般可分为两部分:(l)图像中特定目标区域(器官或组织)的识别;(2)目标区域完整性的描述与提取。相比于其他图像,医学图像的复杂性和多样性,使得传统的基于底层图像信息的分割方法很难取得好的分割结果,而结合了高层视觉先验知识和图像底层信息的主动轮廓模型,符合人类视觉认知事物的一般规律,在计算机辅助诊断中得到了广泛的应用。水平集方法的出现,极大推动了主动轮廓模型的发展。水平集方法和曲线演化模型相结合,克服了传统Snakes模型的很多固有缺陷,大大拓展了主动轮廓模型的应用领域。本文系统的介绍了水平集方法在医学图像分割的应用与发展。
关键词: 医学图像分割 水平集方法 主动轮廓模型
一、概述
水平集方法在图像分割中的应用源于活动轮廓模型。活动轮廓模型方法,是基于局部梯度的一种边界方法。通过对能量函数进行最小化,获得需要的边界,它更多的被用来跟踪变形的运动物体。但是,主动轮廓模型对噪声敏感,更主要的是它得到的结果常依赖于初始化,并且不具有足够拓扑适应性。所以人们又引进了 Balloon 模型,这里对施加到曲线上的外力进行了修改,以减少主动轮廓对弱边缘的敏感性。在基于区域的方法中,有种子区域生长和分裂合并法。利用马尔可夫随机场模型形成的全局标注问题,并对能量函数进行最小化来求解。人们还尝试把轮廓和基于区域的方法结合起来获得新的方法。Zhu S 和 Yuille A[1]介绍了一种区域竞争的方法,把 Snakes/Balloon 的几何特点和区域生长的理论结合起来,取得了一定的效果。自从 Malladi, Sethian 等人[2]把 Level set 法[3]引进到曲线进化中来以后,事实证明 Level set 法在解决曲线进化方程问题时是一个相当有力的工具。Level set 法的优点是:可以处理尖锐的角落,并具有很强的改变拓扑的能力。它可以把具有相当复杂的物体边界分割出来,这是活动轮廓等方法所难以达到的,特别是在处理具有复杂外形的医学图像时,优点更明显。随着近几年医学与信息技术的发展,国内外学者们对水平集方法有了许多的改进,取得了很多令人满意的结果,且在某些器官或组织的分割上,已经达到了临床的要求,甚至比专业医生手工分割的结果还要准确。Q.J.xie[4]等提出一种改进的水平集方法对腹部MRI的肝脏进行分割.孟令旗[5]等提出高斯分布和瑞利分布相结合的方法进行概率密度函数的确定与分析,通过随机极大似然算法SEM把瑞利分布引入到水平集三维分割演化模型中,成功的分割了三维肺CT图像。
二、曲线演化
水平集方法(Level set Method)是在研究曲线演化时提出来的,用于描述曲线的演化过程,它以隐含的方式表达平面闭合曲线,将曲线演化转化为求解偏微分方程的数值问题。
曲线演化理论是研究曲线变化的数学理论。曲线演化理论的目的是仅使用几何度量研究曲线变形,这些几何度量包括单位法向量,曲率。而在参数变形模型中,轮廓运动(变形)依赖的是任意参数化曲线的导数。
曲线演化问题在数学上可以描述为:二维欧式空间R2中的一条光滑闭合的简单曲线沿着其法线方向以一定速度运动,形成以时间为变量的一簇曲线的过程。考虑运动曲线C(s,t)=(X(s,t),Y(s,t)),s为任意参数化变量,t为时间,用N表示描述曲线方向的单位法向矢量,k为描述曲线弯曲程度的曲率,曲线沿法向的演化可由下述偏微分方程表达:

其中,以v(k)被称为速度函数,它决定了曲线上每点的演化速度.曲线C上各点都沿其单位法向方向演化.要指出的是,沿任意方向运动的曲线总可以重参数化为方程(1)的形式,这是因为切向变形仅影响曲线的参数化,不影响其形状和几何属性。
几何活动轮廓模型的基本思想是将图像数据与变形速度相结合,以使演化曲线停止在对象边界上,这种演化采用水平集方法实现,因而,过去对几何模型的大多数研究集中在速度函数的设计上。
三、水平集方法
理论
水平集方法是一种新颖的求解几何曲线演化的方法,它以一种隐含的方式来表达平面闭合曲线或者立体闭合曲线,从而避免了对闭合曲线演化过程中的跟踪,将曲线演化转化成一个纯粹的求偏微分方程数值解问题。另外,水平集方法应用于几何曲线演化时,避免了演化曲线的参数化过程,这样曲线的拓扑结构的变化,即分裂或合并,就变得非常自然。因此,近年来水平集方法逐渐成为研究的热点,并被应用于图像分割,图像平滑,运动分割以及运动目标跟踪,甚至立体视觉和图像的恢复。Osher 和 Sethian[3][7]首次提出用 level set 法来模拟动态曲线和曲面,并以依赖于曲率的速度进化。令γ(t)为一个封闭的参数化曲线,γ(0)是沿着矢量场的法线方向进行传播的初始化曲线,速度依赖于曲率 k ,并给出了传播前沿的偏微分方程的解。假设φ(x,t),x∈R2,是一个矢量函数,在时间t 它的零level set是曲线γt 。进一步假设φ(x,0)=±d(x),其中 d(x)是从 t 到曲线γ0 的距离。如果 x在γ0 里面,就用正号表示,否则,就用负号。令Co§为欧氏平面的初始封闭曲线, C(p,t)是由Co§沿着欧氏法向量向内运动而产生的一系列曲线族。运动的速度认为是曲线曲率k 的矢量函数:

为了根据方程(3)实现曲线的进化,需要考虑利用 Lagrange 方法来产生位置矢量( x, y)= C§的相关运动方程。令φ(x, y,t):R2× [0,T)→R表示曲线C( p,t),那么,根据 level set方法,C( p,t)在时间 t由φ 的零 level set 点所组成:

令φt 为φ对时间的偏微分,由求导的链式法则有:
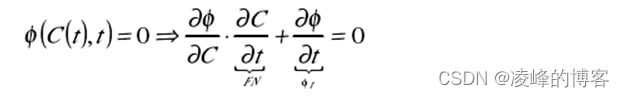
法矢量N =−(∇φ)/|∇φ|,把它代入方程(5),得到φ 的运动方程:
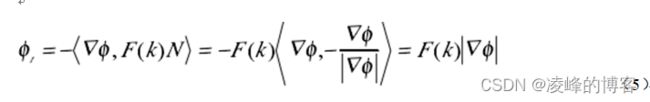
曲线的曲率值可以直接从 level set 函数中估计出来。容易看出 level set 函数沿着C ( p,t)都是同样的值,所以所有的微分都为零(与阶数无关)。对弧长求二阶偏导,得到下面的方程:
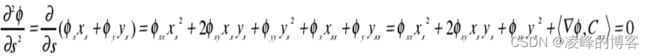
由 Cxy=(xss,yss)=kN,而法向量N=(-ys,xs)= −(∇φ)/|∇φ|,那么:
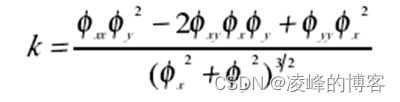
数值解格式
为了实现曲线传播的 level set 方法,必须利用数值近似来求解,一般用有限差分法,使定义在连续空间的偏微分方程能有效地在离散空间解决问题,并具有较强的鲁棒性。
在估计运动方程中出现的法向量、梯度向量和曲率值时,需要用到 level set 函数的一阶和二阶微分,所以要对其利用数值格式进行近似求解。level set 方程 φt = F|∇φ|可以表达成更一般的形式:φt+ H (φx,φy)=0,其中的函数 H (⋅)是哈密尔顿函数。接下去定义六个算子:

一种最简单的数值格式是:
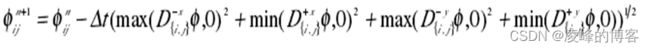
四、水平集方法的关键问题
(l)水平集函数的初始化
通常初始化水平集函数φ(x,y,t)符号离函数d(x,y),其计算量一般较大。因此,如
何快速稳定地计算任意闭合曲面的d(x,y),对于提高水平集方法的效率和稳定性至关重要。
(2)水平集函数的重新初始化
水平集函数通常取为由初始曲线生成的符号距离函数,并且水平集函数在迭代过程中可能发生退化,使它不再保持为符号距离函数,而水平集函数一旦发生退化,则无法得到正确的分割结果。因此为了防止其退化,必须重新初始化水平集函数。保证水平集函数接近符号距离函数,从而保证数值解法的稳定性。符号距离函数必对所有的x,y满足|∇φ|=l,除了保持零水平集和初始化前一样外,重新初始化过程将在所有点上改变水平集函数。因此重新初始化并不改变区域ω和Q\ω重新初始化过程将通过解决一个关于φ(x,y,t)的偏微分方程:
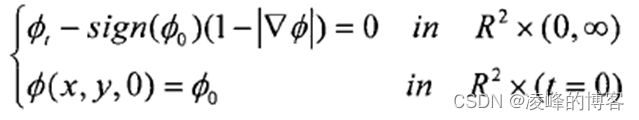
其中φ0为需要重新初始化的函数,这个方程将把函数转化为符号距离函数,并保证零水平集不变。但频繁的执行重新初始过程,不仅会影响水平集函数的演化速度,而且数值误差使零水平集定位不准。因此,如何在演化的过程中保持水平集为符号距离函数这一性质,而无需重新初始化成为当今研究热点。
(3)速度的延拓
水平集的速度函数F,而不仅仅是零水平集上的速度函数,但一般情况下,F只在零水平集上有定义,因此,需要将其延拓到整个解域。尽管已有许多方法对其进行拓展研究,但应用这些拓展速度函数的水平集函数演化方法会失去作为符号函数的特性,从而引起曲率和法向量计算的误差。因此,这些方案往往要求将水平集函数重新初始化为符号距离函数。Adalsteinsson和sethian[83J提出了一种新方法克服了上述不足,该方法是将速度函数拓展问题转化为一个边界值问题,并可通过快速行进法有效解决。Adalsteinsson和sethian指出无需重新初始化的速度函数应满足如下条件:


五、总结
水平集方法将二维闭合曲线或三维闭合曲面的演化问题转化为高维空间中水平集函数曲面演化的隐含方式来求解,适应于对拓扑结构变化的处理,其计算精度高,算法稳定,因而得到广泛应用。近几年来提出的算法大多数是多种算法相结合,但是采取什么样的结合方式才能充分利用各种算法的优点,取得准确的分割效果是人们关注和研究的问题,有待于今后继续研究,以得到更加成熟和适用临床的分割方法"
参考文献
[1] Zhu S, Yuille A. Region competition: Unifying Snakes, region growing, and Bayes/MDL for multi-band image segmentation [A]. International
Conference on Computer Vision (ICCV95) [C]. 1995, 416-423.
[2] Ravikanth Malladi, James A Sethian, Baba C Vemuri. Shape modeling with Front Propagation: A Level Set Approach [J]. IEEE Trans. on
pattern analysis and machine intellegence, 1995-02.
[3] Sethian. J A Level Set Methods [M]. UK: Cambridge University Press, 1996.
[4]QiangjunXie,XufengChen,LiMa,ZekuiZhou.Segmentation for CT image based on improvedlevelsetapproaeh[C],ImageandSignalProeessing,2008.CISP.08.Congress,2008,3:725一728.
[5]孟令旗,林财兴,崔芳芳,骆建珍.基于混合瑞利分布的三维医学图像分割算法[J], 计算机应用与软件,2009,26(l):236一239.
[7] Osher S, Sethian J A. Front propagating with curvature-Dependent Speed: Algorithm Based on Hamilton-Jacobi Formulation [J]. J. ofComputational physics, 1988, 79: 12-49 .
[8].罗嘉,张建伟,陈允杰.结合均值聚类的窄带水平集曲线演化[J],计算机应用与软件,2007,24(7):91一93.
[9] M. Kass, A. Witkin, and D. Terzopoulos, “Snakes: Active contourmodels,”Int. J. Comput. Vis., vol. 1, no. 4, pp. 321–331, Jan. 1987
[10] C. Xu, A. Yezzi, and J. Prince, “On the relationship between parametric and geometric active contours,” inProc. 34th Asilomar Conf. Signals, Syst., Comput., Pacific Grove, CA, Oct. 2000, pp. 483–489