强化学习AI构建实战 - 基于“黄金点”游戏(一)
简介
强化学习(Reinforcement Learning)是机器学习的一种重要技术。本文首先简要介绍了强化学习的概念及思路,然后以Q-Learning算法为例介绍了如何进行训练。随后又介绍了黄金点游戏,并介绍了如何设计实现基于规则的、基于识别的、基于学习的策略BOT来进行比赛。
强化学习
人类如何学习?
在讲解强化学习之前,我们先来了解下人类是如何进行学习的。
我们在Azure Notebook上提供了一个可以线运行的示例环境:HumanLearningDemo.ipynb,使用微软账号登录后就可以克隆并在线运行代码来体验这个环境,也可以将代码复制到本地来运行。
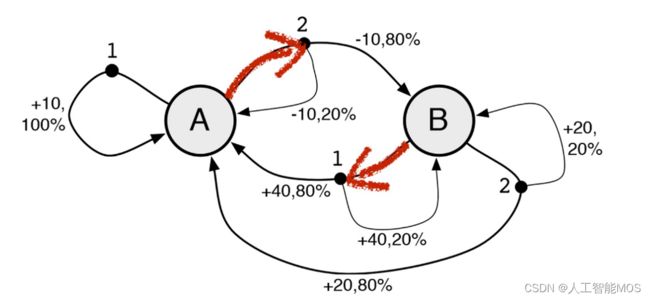
不看代码的话,人对这个示例环境是陌生的,只能输入1或者2,然后可以观察到状态A和状态B,并且在每次输入除了可以看到状态的变化,还可以看到得到了多少分,比如+10分、+40分、-10分等。目标是人需要适应这个新环境,尽可能让自己在环境中得到更多的好处,过得更好。对应于这个示例环境来说,就是要尽可能得到更多的得分。
如何才能得到更多的得分呢,作为一个人类,我们可以考虑下自已会怎么做。
对于刚开始的前几步,由于我们对这个环境一无所知,可能是随意的选择输入1或者输入2。
但是在进行了几步后,我们就可以观察到一些规律,比如有人会观察到状态A的时候输入1总是可以得10分,那我一直输入1就可以一直得分。
也有人愿意进行更大胆的试验,比如状态A时输入2,这时状态会变成B并扣10分,但是再次输入1时可以得到40分,相当于两个动作可以得到30分,比一直输入1更合适,然后再重复试验几次先2后1的组合会发现,这个得30的规律并不总是有效的,所以还要按这个规律出现的概率重新评估是否一直采用先2后1的组合。
| 状态 (A/B) |
动作 (1/2) |
得分 |
|---|---|---|
| A | 1 | +10 |
| A | 2 | -10 |
| B | 1 | +40 |
| A | 1 | +10 |
| A | ... |
总结一下,人类在与这个环境交互的时候会观察并分析:
- 状态会如何随着动作输入进行变化?
- 在某个确定的状态下执行某个确定的动作会得到多少分?
- 怎样才能找到一个策略,可以让我的得分最高?
所以,我们可以理解为人类的学习过程就是不停的在环境中探索,并根据环境变化及自己的收益情况,来不断调整更新自己的经验,最终学到在什么样的情况下怎么做才是最合适的这么一个过程。
在这个环境下最优的策略如下:
| 状态 | 动作 |
|---|---|
| A | 2 |
| B | 1 |
大家可以把真实的环境和自己在环境中摸索的策略进行下比较。
强化学习
接下来我们看一下什么是强化学习。强化学习就是指Agent在一个环境中,为了达到一定的目的(比如延迟的反馈或奖励),不断地采取一系列的动作去尝试与环境进行交互,并在交互中根据反馈或奖励不断的调整策略,最终学到状态和动作的映射关系。
可以看出来,相对于其它机器学习算法,强化学习算法更加现实,更加接近人类的学习过程。
常见的强化学习算法有Q-Learning、策略梯度等,另外还有一些将强化学习和深度学习结合的算法,比如DQN(Deep Q Network)等,另外,前一段时间很火的AlphaGo,以及后来的Alpha Zero,也属于深度强化学习。
Q-Learning
下面我们以Q-Learning为例,来简单介绍下算法的步骤。
Q-Learnig中会用到一个表格,我们叫它为Q Table,也叫Q表。Q表中存放着状态和动作的关系,每个状态是一行,每个动作是一列,表格中的数值代表在这个状态下采用这个动作后可以得到的回报,当然这是个估计值。
算法的迭代过程就是要一步步的调整Q表中的估计值,使得它离现实值越来越近。下图就描述了算法的迭代过程。
我们能不能用Q-Learning来解决刚才上面的问题呢,答案是肯定的。
针对上面的问题,状态可能的取值是A和B,是Q表中的行,动作可能的取值是1和2,是Q表中的列。先初始化Q表,初始值均为0.0
| 1 | 2 | |
|---|---|---|
| A | 0.0 | 0.0 |
| B | 0.0 | 0.0 |
初始状态是A,此时如果输入动作1,新状态还是A,得分是10。套用前面算法中的公式计算Q表中Q(A,1)的值(这里计算时使用的学习率是0.1,未来回报的衰减率是0.9)
Q(A,1) = Q(A,1) + 0.1 * (10 + 0.9 * 0.0 - Q(A,1)) = 0.0 + 0.1 * (10 + 0.9 * 0.0 - 0.0)=1.0
所以此时Q表会变成
| 1 | 2 | |
|---|---|---|
| A | 1.0 | 0.0 |
| B | 0.0 | 0.0 |
接着执行动作2,当前状态是A,执行动作2后状态变成B,得分是-10,再套用公式计算下Q(A,2)
Q(A,2) = Q(A,2) + 0.1 * ( -10 + 0.9 * 0.0 - Q(A,2))=0.0 + 0.1 * ( -10 + 0.9 * 0.0 - 0.0) = -1.0
所以此时Q表会变成
| 1 | 2 | |
|---|---|---|
| A | 1.0 | -1.0 |
| B | 0.0 | 0.0 |
然后再执行动作1,当前状态是B,执行动作1后状态变成A,得分是40,再套用公式计算下Q(B,1)
Q(B,1) = Q(B,1) + 0.1 * ( 40 + 0.9 * 1.0 - Q(B,1))=0.0 + 0.1 * ( 40 + 0.9 * 1.0- 0.0) = 4.09
所以此时Q表会变成
| 1 | 2 | |
|---|---|---|
| A | 1.0 | -1.0 |
| B | 4.09 | 0.0 |
...
在实际的训练过程中,Q-Learning往往会大概率选择当前状态下有最大Q值的动作(和选择动作的策略有关),这会导致算法难以发现有延迟回报的最优动作,往往需要训练很多回合才能达到最好的结果。
我们在Azure Notebooks上提供了用Q-Learning来解决这个问题的示例:Q-LearningDemo.ipynb,大家可以在线运行一下。这个Notebook先分步讲解了Q表是如何更新的,然后又演示了在多回合学习后的Q表是什么样的,最后使用学习到的Q表在未知环境中取得了很高的得分。
“黄金点”游戏介绍
笔者最早接触“黄金点”游戏是通过邹欣老师的软件工程教材《构建之法》及他的博客“创新的时机 – 黄金点游戏”,里面对游戏是这样介绍的:
N个同学(N通常大于10),每人写一个0~100之间的有理数 (不包括0或100),交给裁判,裁判算出所有数字的平均值,然后乘以0.618(所谓黄金分割常数),得到G值。提交的数字最靠近G(取绝对值)的同学得到N分,离G最远的同学得到-2分,其他同学得0分。
同时,邹老师的著作中还提到了这个游戏的来源:
这个游戏是经济学家Richar Thaler构思的,1997年伦敦金融时报进行了一次公开竞猜活动,他们用的系数是2/3,所有人的平均值是18.91。2006年,我是在清华软件学院的一个培训班上第一次玩这个游戏。后来这个游戏成了我演讲和讲课的固定节目,在不少大学的计算机系都玩过。
如果让你参与这个游戏,你会写下哪个数字呢?
通常大家会想,如果所有人随机出数,那么所有人的平均值将是50,50*0.618=31,那是不是出31比较合适呢。但是很多人也会考虑到这一点,如果大家都出了31,那是不是出31*0.618=19更合适呢。
如此循环下去你就会发现,这个数越来越小,那是不是出个很小的数胜率更大呢?也不尽然,很有可能其它参与者并没有想到那么深,你如果出的数过于超前也得不到分。
经过邹老师多次的观察,第一轮获胜的数字离17不远,另外,如果继续玩下去,10轮、20轮,从总体趋势来看,数值会逼近0,但是偶尔也会有小的反弹,然后又继续逼近0。
上图是邹老师在清华大学2008秋季学期连续12次黄金点游戏的记录。
在只有第一名得分、最后一名扣分的规则下,大家更愿意出小一些的数而不是去向上扰动黄金点的值。于是100轮甚至更多轮比赛时,往往变成了大家出了带一堆0的小数,然后比较哪个小数更接近黄金点。
基于此,我们对游戏规则进行了调整,允许每个玩家出两个数,鼓励玩家对黄金点进行扰动。可以一个数出的很大,来保证自己的另一个数比较接近黄金点,这样在失分的情况下也有机会同时得分;也可以两个数都去尝试猜中黄金点,双保险。
整理后新的规则如下:
-
有N个玩家参与游戏
-
每个玩家可以自由选择两个0-100之间的两个有理数(不包括0和100)进行提交
-
所有2*N个数提交后,计算所有数的平均值,然后将平均值乘以0.618得到这一轮的黄金点
-
分别计算所有玩家提交的两个数字与黄金点的算术差的绝对值,值最小者得分,值最大者扣分,其它玩家不得分
具体计分规则如下:
-
N个玩家参与游戏时,离黄金点最近的玩家得N分,最远的扣2分,其它玩家不得分
-
如果多个玩家在一轮内同时离黄金点最近,每个玩家得N分
-
如果多个玩家在一轮内同时离黄金点最远,每个玩家扣2分
-
如果一个玩家在一轮提交的两个数相同并得分或扣分时,只计一次分
-
如果N=1,即只有一个玩家参与游戏时,不记分
-
固定轮数(100轮或更多)比赛后,累加玩家每轮的得分得到总成绩,得分最高者为最终胜出玩家
按照新规则,我们组织一批学生写AI进行了两场比赛,第一场比赛200轮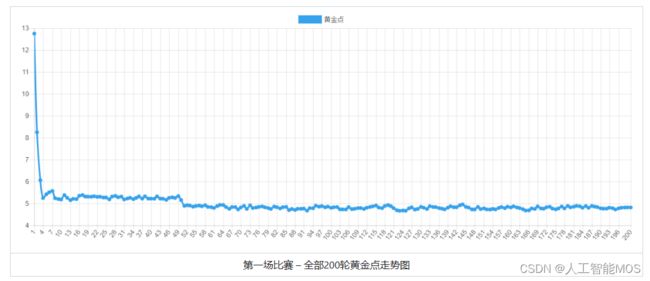
第一场比赛 – 全部200轮黄金点走势图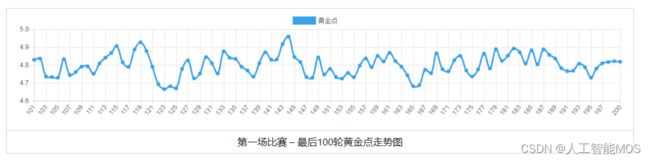 |
| 第一场比赛 – 最后100轮黄金点走势图 |
从第一场比赛可以看出黄金点在刚开始的几轮急速下降,但下降到4~5之间时,一直在细微的波动,说明大家都比较谨慎,没有明显的扰局现象。另外从玩家得分上看,由于大家都比较保守的去预测黄金点,所以得分相对均匀。
随后我们公布了结果,并让大家改进AI,又组织进行了400轮的比赛
第二场比赛 – 全部400轮黄金点走势图 |
| 第二场比赛 – 最后100轮黄金点走势图 |
从第二场比赛可以看出明显第二场要比第一场激烈的多。一个有意思的现象是,在刚开始几轮急速下降后,走势并没有趋向于平稳,而是在有规律的跳动,明显是有玩家在有策略的扰动黄金点。
在事后我们对最终胜出的玩家进行了采访,他们提到在分析第一场的数据时,发现了一个有趣的现象:故意提交大数字的 玩家并没能扰乱黄金点的收敛趋势,反而被扣了很多分。但是他们转念一想,如果大家的结果都在上一轮的黄金点附近波动,那么可以用一个大数来制造扰动,然后根据自己的大数做出相应的调整,给出另一个输出(在比赛中,如果选择 99 作为大数,通常下一轮的 G 会增加 1.1)。
他们迅速实现了想法,并根据第一场的历史数据调整了预测参数。第二场比赛时,黄金点并没有平稳收敛,而是随着他们的扰动策略不断波动,而他们也顺理成章的取得了大把的得分。第二场同样有玩家选择了扰动策略,但却因为对扰动时机、扰动后的预测范围等细节把控不到位,而与胜利失之交臂,可见对细节的掌控也是稳定发挥的基础。