【Multiset类库 旋转Treap(树堆)实现】(仿STL set |名次树 | 随机优先级扩展域)
目录
Treap简介
Treap类的框架
Node结构体的实现
treap构造、析构
默认构造
移动构造
拷贝构造
public主调函数实现(调用private中的辅助函数)
private辅助函数
获取子树大小:getSiz(Node *o)->int
旋转:rotate(Node *&o,int d)->void(核心函数)
插入:insert(Node *&o,int x)->void
删除:erase(Node *&o,int x)->int
销毁:del(Node *o)->void
第k小元素:kth_element(Node *o,int k)->Node *
查询x排名:rank(Node *o,int x,int cur)->int
查找:find(Node *o,int x)->Node *
上紧界:lower_bound(Node *o,Node *f,int x)->Node *
上宽界: upper_bound(Node *o,Node *f,int x)->Node *
遍历:iterate(Node *o,void(*visit)(int val) )->void
树高:height(Node *o)->int
树宽:width(Node *o)->int
Treap简介
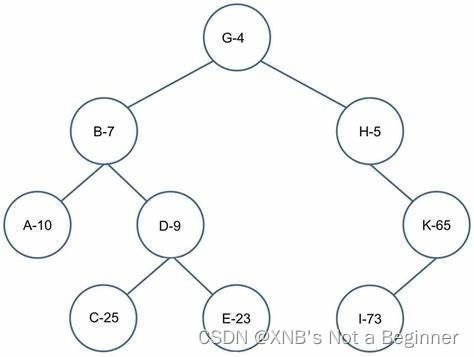
树堆(treap = tree + heap),既是一棵二叉查找树,也是一个二叉堆。
每个节点有一个可比较的关键字对:priority、val。这两个关键字分别维护这个数据结构的(极大)堆性质和BST性质。
二叉堆
二叉堆是基于完全二叉树的基础上,加以一定的条件约束的一种特殊的二叉树
堆总是满足下列性质:
堆中某个节点的值总是不大于或不小于其父节点的值;
堆总是一棵完全二叉树。
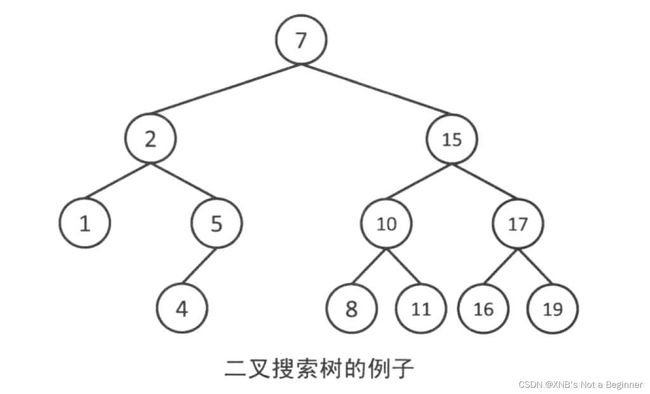
BST
二叉查找树(Binary Search Tree),简写BST,是满足某些条件的特殊二叉树。任何一个节点的左子树上的点,都必须小于当前节点。任何一个节点的右子树上的点,都必须大于当前节点。
treap
普通的BST有很强的不稳定性,在不降或不升序列按序插入中,整棵树会退化成单链表 操作复杂度也从logN提高为N的线性复杂度。而treap通过子树单旋来动态维护这个树形态(像heap一样 在pop实现中,元素下沉和上浮的调整),使树高平衡(基于随机的近似平衡,不是AVL的严格条件:平衡因子绝对值小于等于1)保证删除 查询 插入三大操作的平均期望复杂度保持在logN级别。
同时Treap 通过随机附加域来维护堆的性质,只用到了左旋和右旋,编程复杂度比Splay小, 并且在两者可完成的操作速度有明显优势(名次树实现、SCC连通分量维护与合并等)
Treap类的框架
基本操作
- 构造函数
- 析构函数
- 插入
- 删除
- 查找
- 查询第k小元素
- 查询元素x排名
- 查询最大值
- 查询最小值
- 查询第一个大于等于x的元素
- 查询第一个严格大于x的元素
- 中序遍历
- 查询树的大小
- 查询树是否为空
namespace TREAP{
/*命名空间 防止和STL库命名冲突*/
class Treap{
struct Node{...}
/*内嵌节点结构体*/
public:
Treap(void){...}/*默认构造*/
Treap(const Treap& other){...}/*拷贝构造*/
Treap(Treap&& other){...}/*移动构造*/
~Treap(void){...}/*析构*/
void insert(int x){...}/*插入*/
bool erase(int x){...}/*删除*/
const Node *rank(int x){...}/*排名*/
const Node * kth_element(void){...}/*第k小元素*/
const Node *max_element(void){...}/*最大元素*/
const Node *min_element(void){...}/*最小元素*/
size_t size(void){...}/*树的规模*/
const Node *find(int x){...}/*查询*/
bool empty(void){...}/*是否为空*/
const Node *lower_bound(int x){...}/*上紧边界*/
const Node *upper_bound(int x){...}/*上宽边界*/
void iterate(void(*visit)(int val) ){...}/*(中序)遍历*/
private:
Node *root;/*树根*/
/*...辅助函数*/
};
};
Node结构体的实现
- 构造函数
- 析构函数
- 优先级比较
- 元素大小比较
- 更新子树大小
Node *childs[2];/*二叉链表 数组存储 多路链表方便下标索引*/
int val;/*元素值*/
int prior;/*heap优先级*/
int siz;/*以该节点为根的树的大小*/
int cnt;/*元素重合数(权值)*/
Node(int val,int prior = rand(),/*随机生成优先级修正值*/
int siz = 1,int cnt = 1,
Node *lch = nullptr,Node *rch = nullptr)
:val(val),prior(prior)
,siz(siz),cnt(cnt)
{
childs[0] = lch;
childs[1] = rch;
}
Node(Node&& other) /*移动构造*/
:val(other.val),prior(other.prior)
,siz(other.siz),cnt(other.cnt)
{
childs[0] = other.childs[0];
childs[1] = other.childs[1];/*转让堆内存所有权*/
other.childs[0] = other.childs[1] = nullptr;/*置空防止野指针*/
}
Node(const Node& other) /*拷贝构造*/
:val(other.val),prior(other.prior)
,siz(other.siz),cnt(other.cnt)
{
int i;
for(i = 0;i < 2;++i)/*类似树的遍历 当子树非空 new关键字触发拷贝构造的递归调用*/
childs[i] = other.childs[i]?new Node(*(other.childs[i]))
:nullptr;
}
inline bool operator<(const Node &rhs)const{return prior < rhs.prior;}
/*重载比较运算符 基于优先级比较大小 便于动态调整节点的层级 维护heap的性质*/
inline int cmp(int x)const{return x == val?-1:(x < val?0:1);}
/*基于元素值比较大小 便于元素查询 维护BST的性质*/
inline void maintain(){siz = Treap::getSiz(childs[0])+
Treap::getSiz(childs[1])+1;}
/*用于旋转函数rotate的次调函数,旋转后形态发生变化 更新子树规模*/treap构造、析构
默认构造
Treap(void)
:root(nullptr)
{}移动构造
转移堆内存所有权 绕过析构和拷贝将亡的临时右值对象对系统资源的消耗
Treap(Treap &&other)
:root(*(other.root))
{other.root = nullptr;}拷贝构造
Treap类的拷贝构造通过内嵌结构Node的拷贝构造函数间接实现(由new触发的拷贝构造函数递归调用) 实现逻辑如下
Node(const Node& other)
:val(other.val),prior(other.prior)
,siz(other.siz),cnt(other.cnt)
{
int i;
for(i = 0;i < 2;++i)
childs[i] = other.childs[i]?new Node(*(other.childs[i])):nullptr;
/*类似树的遍历 当子树非空 new关键字触发拷贝构造的递归调用*/
/*子树判空 子树空为递归出口条件*/
} Treap(const Treap &other){
if(root)del(root);/*先销毁原树*/
root = new Node(*(other.root)); /*拷贝root*/
}public主调函数实现(调用private中的辅助函数)
void insert(int x){insert(root,x);}
bool erase(int x){return erase(root,x);}
const Node *kth_element(int x){return kth_element(root,x);}
int rank(int x){return rank(root,x,-1);}
const Node *max_element(void){
Node * o = root,*p;
while((p = o->childs[1]))o = p;
return o;
}
const Node *min_element(void){
Node * o = root,*p;
while(o && (p = o->childs[0]))o = p;
return o;
}
size_t size(void){return getSiz(root);}
const Node *find(int x){return find(root,x);}
bool empty(void){return root == nullptr;}
const Node *lower_bound(int x){return lower_bound(root,nullptr,x);}
const Node *upper_bound(int x){return upper_bound(root,nullptr,x);}
void iterate(void (*visit)(int val)){iterate(root,visit);}private辅助函数
获取子树大小:getSiz(Node *o)->int
获取以传入节点为根的子树大小
空树返回0
static inline int getSiz(Node *o){return o?o->siz:0;}旋转:rotate(Node *&o,int d)->void(核心函数)
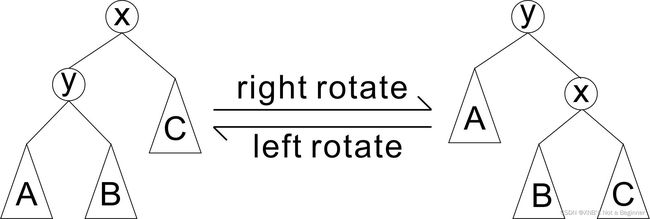
单旋转函数 在删除 插入函数的递归回溯中自底向上的调整树的形态 使一直满足堆的性质
int d为需要提拔的是左子树还是右子树 | 左:d == 0 -> zig 、 右:d == 1 -> zag
传入引用指针 因为树根会在旋转过程中发生变化
void rotate(Node *&o,int d){
Node *k = o->childs[d^1];
o->childs[d^1] = k->childs[d];
k->childs[d] = o;
o->maintain();k->maintain();
o = k;
}插入:insert(Node *&o,int x)->void
插入函数:传入引用指针 也可以用接受回传指针的方式 防止局部指针变量的销毁和堆内存地址丢失
在递归过程中 维护子树大小和元素数目
void insert(Node *&o,int x){
if(nullptr == o){o = new Node(x);return;}
++(o->siz);int d = o->cmp(x);
if(~d){++(o->cnt);return;}
insert(o->childs[d],x);
if(*(o->childs[d]) > *o)rotate(o,d^1);
}删除:erase(Node *&o,int x)->int
删除函数 返回值为删除失败与否 | 成功:1 失败:0
int erase(Node *&o,int x){
if(!o)return 0;
int d = o->cmp(x);
if(!(~d))if(erase(o->childs[d],x))--(o->siz);
else{
if(!o->childs[0]){Node *t = o;o = o->childs[0];delete t;return 1;}
else if(!o->childs[1]){Node *t = o;o = o->childs[1];delete t;return 1;}
int dd = ~(int)(*(o->childs[0]) < *(o->childs[1]));
rotate(o,dd);erase(o->childs[dd],x);
}
}销毁:del(Node *o)->void
销毁函数 后序遍历实现
void del(Node *o){
if(o){
del(o->childs[0]);del(o->childs[1]);
delete o;o = nullptr;
}
}第k小元素:kth_element(Node *o,int k)->Node *
top/bot-k函数 通过维护的每个子树的大小进行递归 得到答案
Node *kth_element(Node *o,int k){
if(k < o->siz+1)return kth_element(o->childs[0],k);
else if(k > o->siz + o->cnt)
return kth_element(o->childs[1],k-(o->siz + o->cnt));
else return o;
}查询x排名:rank(Node *o,int x,int cur)->int
排名函数 查询给定元素x所处的排名
cur为当前递归层级内位于x前面的元素个数
int rank(Node *o,int x,int cur){
if(!o)return -1;
if(x == o->val)return getSiz(o->childs[0])+cur+1;
if(x < o->val)return rank(o->childs[0],x,cur);
else return rank(o->childs[1],x,cur+o->siz+o->cnt);
}查找:find(Node *o,int x)->Node *
查询给定元素x 递归实现
Node *find(Node *o,int x){
if(!o)return nullptr;
if(o->val == x)return o;
if(o->val < x)return find(o->childs[0],x);
else return find(o->childs[1],x);
}上紧界:lower_bound(Node *o,Node *f,int x)->Node *
上紧界查询 第一个大于等于给定元素x的元素
Node *f 为x的父节点
Node *lower_bound(Node *o,Node *f,int x){
if(!o)return f;
if(o->val == x)return o;
if(o->val < x)return lower_bound(o->childs[0],o,x);
return lower_bound(o->childs[1],o,x);
}上宽界: upper_bound(Node *o,Node *f,int x)->Node *
上宽界查询 第一个严格大于给定元素x的元素
Node *upper_bound(Node *o,Node *f,int x){
if(!o)return f;
if(o->val <= x)return lower_bound(o->childs[0],o,x);
return lower_bound(o->childs[1],o,x);
}遍历:iterate(Node *o,void(*visit)(int val) )->void
遍历函数 采用中序遍历 可以打印有序序列
visit 是void(*)(int)型的函数指针 对节点的数据域val操作
void iterate(Node *o,void(*visit)(int val)){
if(o){
iterate(o->childs[0],visit);
visit(o->val);
iterate(o->childs[1],visit);
}
}树高:height(Node *o)->int
求树的最大深度 也为树根到叶子节点的最大外部路径长度 体现了DC递归思想
int height(Node *o){
if(!o)return 0;
if(!o->childs[0] && !o->childs[1])return 1;
return 1 + std::max(height(o->childs[0]),height(o->childs[1]));
}树宽:width(Node *o)->int
求树的纵向宽度 BFS在线记录实现
int width(Node *o){
if(!o)return 0;
int m = 0;
std::queue Q;Q.push(o);
while(!Q.empty()){
int s = Q.size();
m = std::max(m,s);
while(s--){
Node *o = Q.front();Q.pop();
int i;
for(i = 0;i < 2;++i)
if(o->childs[i])
Q.push(o->childs[i]);
}
}
return m;
}