蓝桥杯AcWing学习笔记 9-1复杂DP的学习（上）

蓝桥杯

我的AcWing

题目及图片来自蓝桥杯C++ AB组辅导课

复杂DP（上）

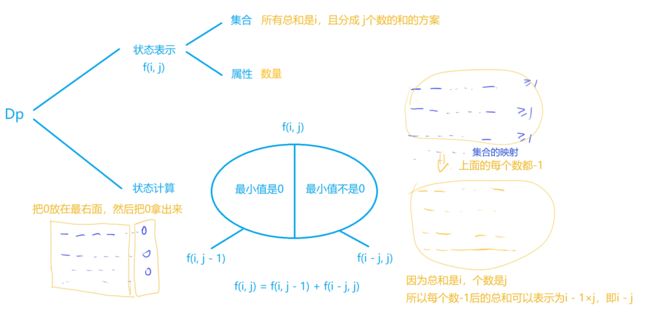
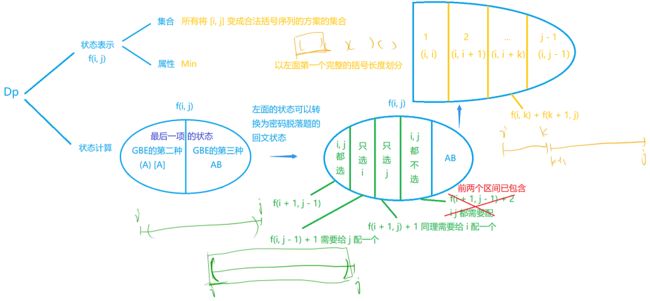
非传统DP问题思考方式，全新的DP思考方式：从集合角度来分析DP问题——闫式DP分析法

例题

AcWing 1050. 鸣人的影分身

整数划分的变形题。

$M$个查克拉，$N$个影分身，当7个查克拉分配在3个影分身的时候，可以有8种方案。

暴搜dfs（AC）

相当于是m个球，放n个盒子，每个盒子最少放0个球的问题

暴力枚举每个盒子放多少个球，为了方便从左到右的球的数量从小到大递增，dfs过程中需要添加多start作为开始枚举的位置

import java.util.Scanner;
/*
	参考AcWing小呆呆大佬
*/
public class Main {
    
    static int n;
    static int m;
    static int ans;
    
    public static void main(String[] args) {
        Scanner sc = new Scanner(System.in);
        int T = sc.nextInt();
        while(T -- > 0) {
             ans = 0;
             m = sc.nextInt(); // 能量
             n = sc.nextInt(); // 分身个数
             dfs(1, m, 0);
             System.out.println(ans);
        }
    }
    
    // 枚举第u个盒子 nums表示当前剩下多少个能量 从start数开始枚举
    private static void dfs(int u, int nums, int start) {
        if (u == n + 1) {
            if (nums == 0) {
                ans ++;
            }
            return;
        }
        if (start > nums) return; // 剪枝
        for (int i = start; i <= nums; i ++) {
            dfs(u + 1, nums - i, i);
        }
    }
}

闫式DP分析法（AC）

时间复杂度 $O(N^2)$

import java.util.Scanner;
import java.util.Arrays;

public class Main {
    
    static final int N = 11;
    static int[][] f = new int[N][N];
    
    public static void main(String[] args) {
        Scanner sc = new Scanner(System.in);
        int T = sc.nextInt();
        while (T-- > 0) {
            int m = sc.nextInt();
            int n = sc.nextInt();
            
            for(int i = 0; i <= m; i ++) Arrays.fill(f[i], 0);
            f[0][0] = 1; // 和为0 0个数  也是一种方案
            
            for (int i = 0; i <= m; i++) { // 和为0 1个数 和为0 2个数 都是有意义的 所以i从0开始枚举
                for (int j = 1; j <= n; j++) { // f[0][0]已经被初始化过 j可从1开始枚举
                    f[i][j] = f[i][j - 1]; // 最小值为0，任意条件可取
                    if (i >= j) f[i][j] += f[i - j][j]; // 最小值不为0 须在i >= j才能取到
                }
            }
            
            System.out.println(f[m][n]);
        }
    }
}

---

AcWing 1047. 糖果

本题是一个选择模型的题，也就是背包问题。

选择的n件产品中每件尽量包含更多的糖果，且糖果总数是k的倍数。

换句话来说就是，给我们n个数，然后在n个数中能凑成k的倍数，且和最大的值就是我们要选的。

背包问题是总和不能超过总体积，本题是总和一定要是k的倍数。

闫式DP分析法：

import java.util.Scanner;
import java.util.Arrays;

public class Main {
    
    static final int N = 110;
    static int[][] f = new int[N][N];
    
    public static void main(String[] args) {
        Scanner sc = new Scanner(System.in);
        int n = sc.nextInt(), k = sc.nextInt();
        
        for (int i = 0; i <= n; i++) Arrays.fill(f[i], Integer.MIN_VALUE); // 初始化为负无穷
        f[0][0] = 0; // 只有0个数 总数为0才有意义
        for (int i = 1; i <= n; i++) {
            int wi = sc.nextInt();
            for (int j = 0; j < k; j++) {
                f[i][j] = Math.max(f[i - 1][j], 
                f[i - 1][(j + k - wi % k) % k] + wi); // 这里要对第二个公式进行处理 否则可能会出现负余数
            }
        }
        System.out.println(f[n][0]); // 我们求的数要%k为0
    }
}

第七届2016年蓝桥杯真题

AcWing 1222. 密码脱落

C++A/C组第9/10题

区间dp

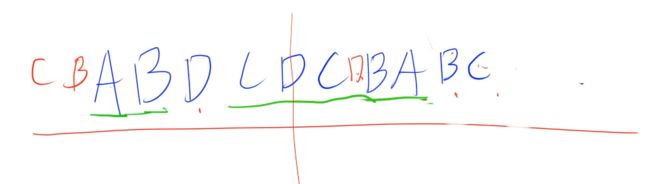
就是现在给我们一个不是回文串的字符串ABCA，问我们至少需要几个字母可以将它变为回文串。

想要一个字符串变成回文串，我们要取一个中轴，从两边以一一对比进行配对，如果一边有一个字母落单，那么另一边就需要一个字母来配对，最终配对的数量就是我们要求的值，其实这个问题等价于：这个字符串删掉几个字母可以变为回文串，这两个答案是一样的；所以答案为：ans = 总长度 - 最长回文子序列长度

我们可以选择补全，或者直接将落单的字母删掉。

那么我们怎么找到一个字符串的最长回文子序列呢？

注意，是求回文子序列，不是回文串！因此是有可能不连续的。

闫式DP分析法

import java.util.Scanner;

public class Main {
    
    static final int N = 1010;
    static int[][] f = new int[N][N];
    
    public static void main(String[] args) {
        Scanner sc = new Scanner(System.in);
        String str = sc.next();
        int n = str.length();
        
        char[] s = str.toCharArray();
        for (int len = 1; len <= n; len++) { // 先循环长度
            for (int l = 0; l + len - 1 < n; l++) {
                int r = l + len - 1;
                if (len == 1) f[l][r] = 1;
                else {
                    if (s[l] == s[r]) f[l][r] = f[l + 1][r - 1] + 2;  // 第一种状态
                    if (f[l][r - 1] > f[l][r]) f[l][r] = f[l][r - 1]; // 第二种状态
                    if (f[l + 1][r] > f[l][r]) f[l][r] = f[l + 1][r]; // 第三种状态
                }
            }
        }
        
        System.out.print(n - f[0][n - 1]); // 总长度 - 最长回文子序列长度
    }
}

第六届2015年蓝桥杯真题

AcWing 1220. 生命之树

JavaB组第10题

树形dp

本题就是在一棵树中找到最大权值和的连通块。

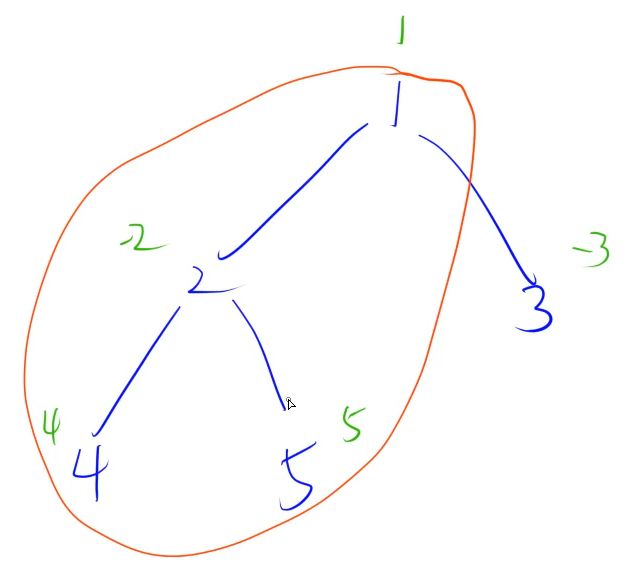
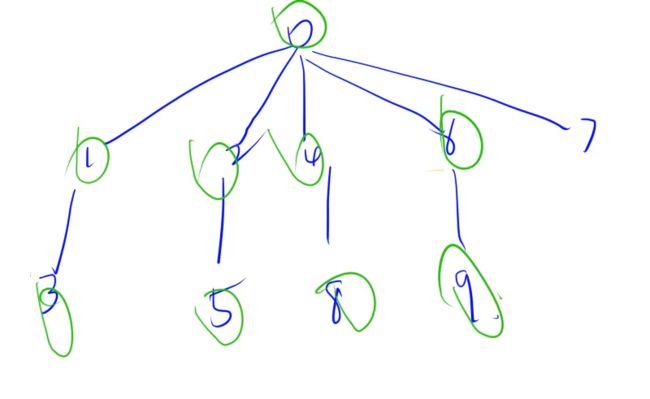
看第一个样例：

连通块最大值为9。

树形dp我们一般用递归来做，每次以子树为单位来计算，先递归把所有子节点的值算出来，然后用子节点的值算出根节点的值。

不管是哪个连通块，一定会有一个最高点，也就是离根节点最近的点/就是根节点，

f(u)：在以u为根的子树中包含u的所有连通块的权值的最大值。

假设k是最高点，那么f(k)一定就是最优解。

所以只要求完所有f(u)，那么最优解就是在f(u)中取Max。

如何求f(u)呢？如下图：

假设u的权值是$W_u$，我们只需要取每一个子节点$f(S_i)$的$Max$即可，如果此子节点是负数那我们直接舍弃掉。

时间复杂度 $O(N)$

import java.util.Scanner;
import java.util.Arrays;

public class Main {

    static final int N = 100010, M = N * 2; // 因为是一颗无向树，所以边数要双向建
    static int[] w = new int[N];   // 权值
    static int[] h = new int[N];   // 邻接表
    static int[] e = new int[M];   // 此节点的值
    static int[] ne = new int[M];  // 此节点下一个节点的下标
    static long[] f = new long[N]; // 状态数组
    static int idx; // 存储当前已经用到了哪个点

    public static void main(String[] args) {
        Scanner sc = new Scanner(System.in);
        int n = sc.nextInt();
        Arrays.fill(h, -1);

        for (int i = 1; i <= n; i++) w[i] = sc.nextInt(); // 读入权值
        for (int i = 0; i < n - 1; i++) { // 加n-1条边
            int a = sc.nextInt(), b = sc.nextInt();
            add(a, b);
            add(b, a);
        }

        dfs(1, -1);

        long res = f[1];
        for (int i = 2; i <= n; i++) res = Math.max(res, f[i]);
        if (res < 0) System.out.println(0);
        else System.out.println(res);
    }

    private static void add(int a, int b) {
        e[idx] = b;
        ne[idx] = h[a];
        h[a] = idx++;
    }

    private static void dfs(int u, int father) {
        f[u] = w[u];
        for (int i = h[u]; i != -1; i = ne[i]) {
            int j = e[i];
            if (j != father) { // 利用存的父节点 防止往回遍历
                dfs(j, u);
                f[u] += Math.max(0, f[j]);
            }
        }
    }
}

AcWingAC，蓝桥杯最多能拿50分。

这题蓝桥卡数据，如果值是负值则输出0，题中也没说，y总的C++代码可以满分，但是java的后一半数据运行错误，不知道哪里有问题。

区间dp拓展题

AcWing 1070. 括号配对

区间dp

闫式DP分析法

我们在区间dp中，分情况是不重不漏的，但是由于某一种情况并不一定存在某种状态恰好表示它，所以在这种情况下，我们要找到一个能覆盖当前这一类情况的状态就可以了，这是一个难点。

import java.util.Scanner;

public class Main {
    
    static final int N = 110, INF = 100000000;
    static int[][] f = new int[N][N];

    public static void main(String[] args) {
        Scanner sc = new Scanner(System.in);
        String s = sc.next();
        int n = s.length();

        for (int len = 1; len <= n; len ++ )
            for (int i = 0; i + len - 1 < n; i ++ )
            {
                int j = i + len - 1;
                f[i][j] = INF;
                // 左边情况
                if (is_match(s.charAt(i), s.charAt(j))) f[i][j] = f[i + 1][j - 1];
                if (j >= 1) f[i][j] = Math.min(f[i][j], Math.min(f[i][j - 1], f[i + 1][j]) + 1);

                for (int k = i; k < j; k ++ ) // 右边情况
                    f[i][j] = Math.min(f[i][j], f[i][k] + f[k + 1][j]); // 左边右边再取最小
            }
        
        System.out.print(f[0][n - 1]);
    }
    
    // 判断是否属于左边情况
    private static boolean is_match(char l, char r) {
        if (l == '(' && r == ')') return true;
        if (l == '[' && r == ']') return true;
        return false;
    }
}

树形dp拓展题

AcWing 1078. 旅游规划

树形dp

有多少个点的边权在树的直径上。

边的数量最多的路径就是树的直径。

分析第一个样例，总共有三个直径：

圈绿的数都在直径上，所以将它们从大到小输出。

在之前的图论中，我们证明了求树的直径的方法，在树形dp中，我们用一种更一般的方法。

我们从直径的定义出发去找直径，任何一条路径都存在唯一的一个最高点，我们以路径的最高点来分类，第1个表示所有路径的最高点在第1个点的路径，第2个表示所有路径的最高点在第2个点的路径，以此类推，一共可以分成$N$个集合：

$d_i$ 表示从 $i$ 这个点往下走的最大值，我们只需要对每个点求一个最大值，再求一个次大值，最大值和次大值有可能相同，此时两个值相加，对于每个点都取一个$Max$，最终的最大值就是我们树的直径，全部遍历一遍时间复杂度是 $O(N)$ 。

本题要求的是哪些点在这个最大路径上，也就是树的直径。

判断这个点是否在树的直径上，我们只需要看一下这个点出发的所有路径的最大值和次大值并相加，判断是否等于直径长度即可。

我们还要再求一下从这个点出发往上走的最大长度是多少，我们需要两遍dfs。

这题有点难理解。