算法总结——前缀和、二维前缀和

一维前缀和

前缀和总览：

一维前缀和的作用：用于快速求出某个区间所有元素的和。
首先我们先看一个题了解前缀和的应用场景：

如果我们不使用前缀和我们可能首先会想到暴力的做法，直接遍历区间l到r，求和输出。

#include
const int Max = 1e5 + 10;
int arr[Max];
int n,m;
int main()
{
	scanf("%d%d", &n, &m);
	for(int i = 1; i <= n; i++)
	{
		scanf("%d", &arr[i]);
	}
	while(m--)
	{
		int l, r;
        int sum = 0;
        scanf("%d%d", &l, &r);
        for(int i = l; i <= r; i++)
        { 
          //最坏的情况，循环n次,就是求整个区间的和，其时间复杂度为O(n)
          sum += arr[i];
        }
        printf("%d\n",sum);
	}
	return 0;
}

暴力法遍历求区间和的时间复杂度是O(n)，又因为查询m次，所以整个算法时间复杂度为O(m*n)，如果n和m的数据量稍微大一点就有可能超时，而我们如果使用前缀和的方法来做的话，可以将求区间和的操作的时间复杂度降为O(1)，大大提高了运算效率。
前缀和的做法：

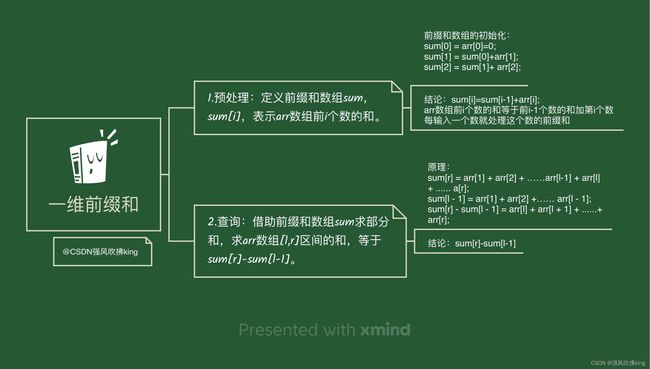
原理：

注意：
arr数组和sum数组都从下标为1开始处理。(后面的二维前缀和差分也是这个原理，不在重复)
①这样对于arr数组可以避免频繁的进行下标转换（因为我们人想的第一个数在计算机中的下标为0）。下标为0的元素直接初始化为0，不影响最后结果。
②对于前缀和数组sum便于使用公式sum[i]=sum[i-1]+arr[i]，避免处理边界，如果不从下标1处开始使用，上述公式是用不了的。例如：sum[0]=sum[-1]+arr[0]。
用前缀和来处理先前题目，代码展示：

#include
using namespace std;
const int Max=1e5+10;
int n,m;
int arr[Max],sum[Max];//全局变量，暗含sum[0]=0,arr[0]=0;
int main()
{
    scanf("%d%d",&n,&m);
    for(int i=1;i<=n;i++)
    {
        scanf("%d",&arr[i]);//arr数组的初始化
        sum[i]=sum[i-1]+arr[i];//前缀和数组sum的预处理
    }
    while(m--)
    {
        int l,r; 
        scanf("%d%d",&l,&r);
        //查询的时间复杂度为O(1)
        printf("%d\n",sum[r]-sum[l-1]);
    }
    return 0;
}

查询的时间复杂度为O(1)，整个算法的时间复杂度为O(n+m)，n是数组长度，m是查询次数。前缀和数组sum可以不创建，直接让arr数组变成自己的前缀和数组（看个人需要,差分要用到）。

for(int i=1;i<=n;i++)
{
	scanf("%d",&arr[i]);//arr数组的初始化
	arr[i]+=arr[i-1];//自己变成前缀和数组
}

二维前缀和

二维前缀和的作用：快速求出某个子矩阵的和。
二维前缀和步骤：

①预处理详细步骤（图解）
从之前的一维前缀和可以很容易推导二维前缀和，就是多了一个方向。
我们首先来看一张坐标图：

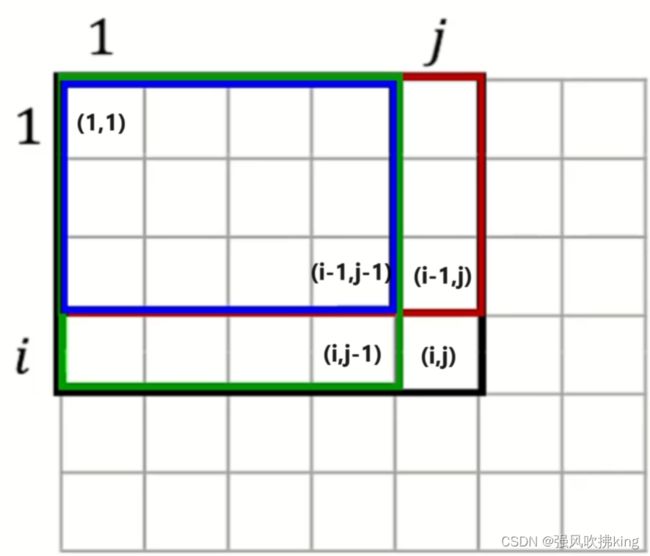
sum[i][j]表示第1行1列到第i行j列所围成矩形的元素和。
从图中我们很容易看出，整个外围黑色矩形面积sum[i][j] = 红色面积sum[i - 1][j] + 绿色面积sum[i][j - 1] - 重复加的蓝色的面积sum[i - 1][j - 1] + 小方块的面积arr[i][j]
所以我们可以得出预处理的公式为：
sum[i][j]=sum[i-1][j]+sum[i][j-1]-sum[i-1][j-1]+arr[i][j]

黑色矩形的面积（子矩阵） = 整个外围红色面积sum[x2, y2] - 蓝色面积sum[x2, y1 - 1] - 绿色面积sum[x1 - 1, y2] + 重复减去的面积 sum[x1 - 1, y1 - 1]
②查询：
sum[x2][y2]-sum[x1-1][y2]-sum[x2][y1-1]+sum[x1-1][y1-1];

例题：
输入一个n行m列的整数矩阵，再输入q个询问，每个询问包含四个整数x1, y1, x2, y2，表示一个子矩阵的左上角坐标和右下角坐标。
对于每个询问输出子矩阵中所有数的和。
输入格式：
第一行包含三个整数n，m，q。
接下来n行，每行包含m个整数，表示整数矩阵。
接下来q行，每行包含四个整数x1, y1, x2, y2，表示一组询问。
输出格式：
共q行，每行输出一个询问的结果。
数据范围：

1≤n,m≤1000,
1≤q≤200000,
1≤x1≤x2≤n,
1≤y1≤y2≤m,
−1000≤矩阵内元素的值≤1000

输入样例：

3 4 3
1 7 2 4
3 6 2 8
2 1 2 3
1 1 2 2
2 1 3 4
1 3 3 4

输出样例：

17
27
21

代码：

#include
using namespace std;
const int Max=1010;
int n,m,q,arr[Max][Max],sum[Max][Max];
int main()
{
    cin>>n>>m>>q;
    for(int i=1;i<=n;i++)
      for(int j=1;j<=m;j++)
    	{
        	cin>>arr[i][j];//初始化arr数组，同时完成前缀和数组sum
        	sum[i][j]=sum[i-1][j]+sum[i][j-1]-sum[i-1][j-1]+arr[i][j];
    	}
    while(q--)//查询
    {
        int x1,y1,x2,y2;
        cin>>x1>>y1>>x2>>y2;
        cout<<sum[x2][y2]-sum[x2][y1-1]-sum[x1-1][y2]+sum[x1-1][y1-1]<<endl;
    }
    return 0;
}

前缀和数组sum可以不创建，直接让arr数组变成自己的前缀和数组（看个人需要，差分要用到）。

for(int j=1;j<=m;j++)
{
	cin>>arr[i][j];
	arr[i][j]+=sum[i-1][j]+sum[i][j-1]-sum[i-1][j-1];
}