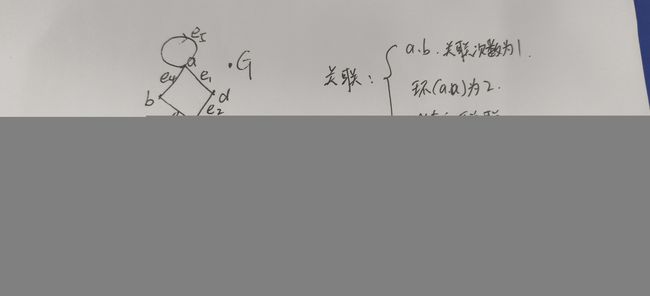离散数学(屈婉玲)图论<一>
嗯~,原本想从第一章开始分享的,但一想马上要期末考试了,后面的占比可能会更大些,所以,从比较难得图论开始吧。
刚开始用这个app,不咋地会用(尬笑),可能没法像其他大佬们那样看着好看,不过放心,我会努力学学的,努力像他们看齐!
<一>图
图在离散数学中通常用个有序的二元数组
(V代表顶点的集合,他的元素为顶点
E为边集,他的元素为边)
图包括两种
- 无向图(没有方向,没有箭头)
- 有向图(有方向,右箭头)
对于无向图的相关知识点
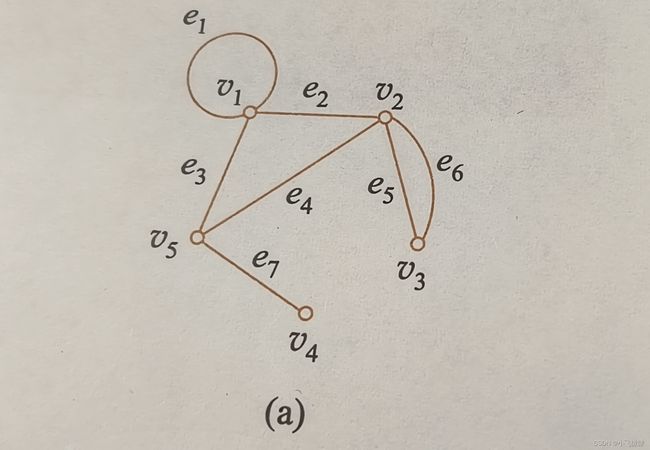
他的V={V1,V2,V3,V4,V5}
E={e1,e2,e3,e4,e5,e6,e7}
其中V顶点的个数又称为“阶”,顶点为几阶的图就称为几阶图。(所以该图就是5阶图)。
标定图:如果对每个边和每个顶点都命名的话(通常用字母或数字,当然字母可以带下标),则该图为标定图。本图就是标定图。
零图:一条边也没有的图。n阶零图记作Nn.
(一阶零图成为平凡图吼)(就是只含有一个点哈)
空图:顶点集为空集的图(画不出来,但通常在以后图运算过程中可能会产生。
为了更加直观理解有点难理解知识点,我画了下图。
课本上是那么定义的。
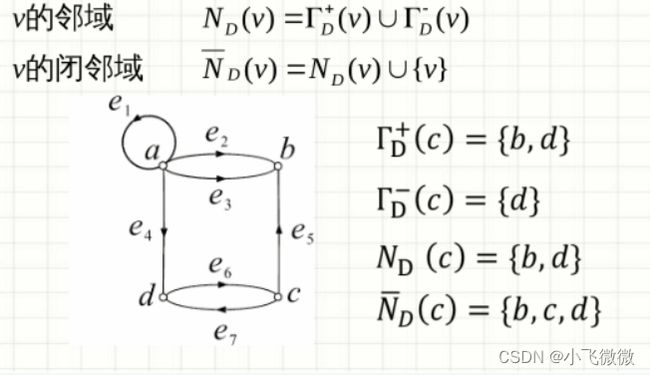
邻域闭邻域
对于V1邻域就是V5和V2,(与V1通过边相连的点就是)
闭邻域就是加上他自己这个点,即v1闭邻域为v1,V5,v2。
关联集
还从上面那个图来看,V1关联集就是e1,e2,e3。(就是与该点所就接的所有边构成的集合。
后继元素,先驱元素,邻域,闭邻域
后继元素:TD十()表示,就是从该点出发到另外一个顶点,那个另外一个顶点构成的集合。
先驱元素:就是从外面顶点指向该顶点所构成的外面顶点集合。(通常用TD一()表示)。
提醒一下哈,字母我有的尊嘟打不出来(呜呜呜),以记的以图上的为准吼,记得看图哦!
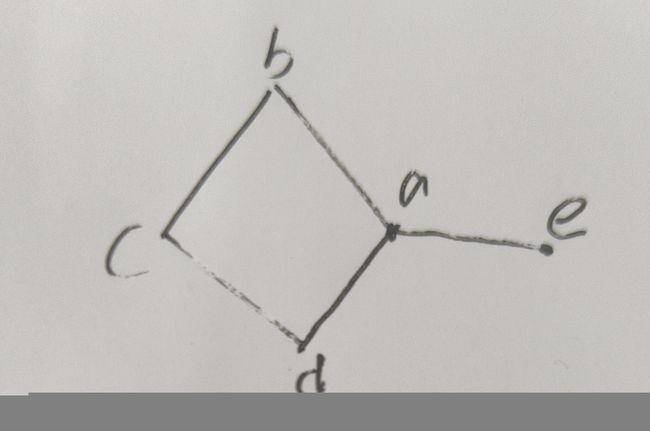
度数(度常用d()表示):就是通过该点有多少条边(还从上图来看,点a度数就是5吼,离散数学中,环通常规定为两条边哒。)
出度和入度:
出度:从该点出发向外的边数。例上图中的c出度为2
入度:该点接收外来边的边数。例上图中的c入度为1。
平行边:
其中含平行边的图称为多重图
平行边的条数称作他的"重数"吼。
最大度最小度悬挂点,边问题
最大度就是在整个图中,所有顶点中度数最大的那个顶点的度数。
同理最小度就是所有顶点中度数最小的那个顶点的度数。
其中,e为悬挂点,ae这条边称作悬挂边。(定义上面图中有,不难理解的).
握手定理(重要☆)
握手定理:
- 任何无向图中,所有顶点度数之和等于边数的2倍
- 任何有向图中,所有的度数和等于边数2倍,且入度和等于出度和,等于边数。
- (推论)任何图中(无向或有向),奇度顶点个数为偶数。
可图化和可简单图画
对于一组数而言,如果按照特定的规则可以构建出一个无向图,那么我们就说这组数是可图化的。
简单图是一种特殊的图。如果一个图中既没有环,也没有多重边,则这样的图被称为简单图。
(这个知识点貌似不是特别重要)
图的同构:点相同,边相同。
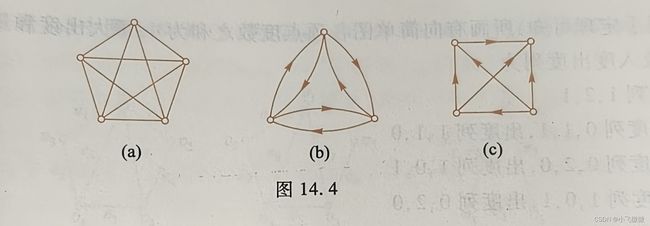
完全图和竞赛图
完全图:每个顶点与其他顶点均相连。
a为无向完全图
b为有向完全图
C为n阶竞赛图。
K一正则图:任意顶点度数均为K的无向简单图。
母图与导出子图
首先给出定义:
无向母图 G=(V,E) , V 为所有顶点, E 为所有边。
子图 G′=(V′,E′) , V′∈V,E′∈E 。
生成子图 G″=(V″,E″) , V″=V,E″∈E 。
导出子图 G‴=(V‴,E‴) , V‴∈V ,并且和 V‴ 相关联的边都得出现。如果选了 v1,v2 ,那么就得选 v1,v2 之间的边。
补图,自补图,删除边,点,加新边
自补图是相对于完全图来说,把一个图添加边是的其成为完全图所构成的图叫补图。 当一个图和它的补图同构时,为自补图。
例如
1+2 =3 ,
1的相对于3的补是2.
1+1=2
这时候1 相对于2的补是1,这首1和1的补相同,1就是自补的。第二个图有多余节点不能算
删除边,点就是表面意思。
收缩:像图中我画的那样,收缩e1就是把e1边删去,c点直接与a重合,只剩e2
通路与回路
1、通路:
顶点与边的交替序列
2、起点, 终点, 通路长度
第一个点是起点,最后一个点是终点
通路长度 |Γ| = l
3、回路
首尾相连的通路,起点与终点是同一个点
4、简单(复杂、初级)通(回)路
简单通路: 没有重复边的通路
简单回路: 没有重复边的回路
复杂通路: 有重复边的通路
复杂回路: 有重复边的回路
初级通路(路径)是每个结点只经过一次
简单通路是边只经过一次
只满足边各异,为简单通路
既满足边各异又满足顶点各异,为初级通路
初级回路(圈):(所有顶点,边均各异,最后可以回到原来那个点)(回不到则称为初级通路)
将长度为奇数的圈称作奇圈,长度为偶数的圈为偶圈。
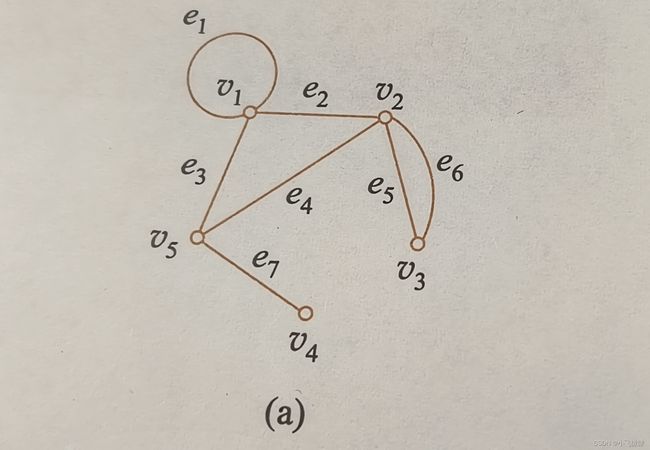
像e3,e6,e7构成了初级回路
e3,e6,e5,e4 也是初级回路
e3,e6,e5构成初级通路
回路是通路的特殊情况,初级通路(回路)必然是简单通路(回路),反之则不真。
有重复边出现的,则称之为复杂通路
对于初级通路,长为1的圈只能用环生成,长为二的圈只能由平行边生成,因此,在简单无向图中,圈的长度至少为三。
不知不觉中,已经爆肝了一个晚自习。总结一下,打字尊都很累(呜呜呜)。虽然很累,但感觉这些知识点一辈子都不会忘了(嘻嘻)。希望对大家有帮助!!!如果哪个写错的话,或者有更容易理解的思路,希望大家可以在评论区里分享出来嘛!明天会更其他更多内容吼,可能还有今天这些知识点的其他补充哒!