论文笔记（十四）：PoseRBPF: A Rao–Blackwellized Particle Filter for 6-D Object Pose Tracking

文章概括

作者：Xinke Deng, Arsalan Mousavian, Yu Xiang, Member, IEEE, Fei Xia, Member, IEEE, Timothy Bretl, Member, IEEE, and Dieter Fox, Fellow, IEEE
来源：IEEE TRANSACTIONS ON ROBOTICS
原文：https://ieeexplore.ieee.org/stamp/stamp.jsp?tp=&arnumber=9363455
代码、数据和视频：https://github.com/NVlabs/PoseRBPF
系列文章目录：
上一篇：
论文笔记（十三）：Differentiable Particle Filters: End-to-End Learning with Algorithmic Priors
下一篇：

摘要

从视频中追踪物体的六维姿态为机器人执行不同的任务（如操纵和导航）提供了丰富的信息。在这篇文章中，我们在Rao-Blackwellized粒子过滤框架中制定了6维物体姿态跟踪问题，其中物体的3-D旋转和3-D平移是解耦的。这一因素化使得我们的方法，即PoseRBPF，能够有效地估计物体的3-D平移以及3-D旋转的全部分布。这是通过细粒度的旋转空间离散化和训练一个自动编码器网络来构建离散化旋转的特征嵌入编码库来实现的。因此，PoseRBPF可以追踪具有任意对称性的物体，同时仍然保持足够的后验分布。我们的方法在两个六维姿势估计基准上取得了最先进的结果。我们将我们的实现开源于https://github.com/NVlabs/PoseRBPF。

索引词——计算机视觉，状态估计，六维物体姿势跟踪。

1. 介绍

从摄像机图像中估计物体的6维姿势，即物体相对于摄像机的3维旋转和3维平移，是机器人应用中的一个重要问题。例如，在机器人操纵中，物体的六维姿态估计为机器人提供了规划和执行抓取的关键信息。在机器人导航任务中，三维物体的定位为规划和避开障碍物提供了有用的信息。由于其重要性，机器人界[5]、[9]、[67]、[75]和计算机视觉界[21]、[37]、[53]都为解决六维姿势估计问题做出了各种努力。

传统上，物体的六维姿态是使用局部特征或模板匹配技术来估计的，其中从图像中提取的特征与为物体的三维模型生成的特征或视点模板相匹配。然后，利用这些局部特征的2-D-3-D对应关系或通过选择最佳匹配视角来恢复6-D物体的姿势[9], [20], [21]。最近，机器学习技术被用来检测关键点或学习更好的图像特征进行匹配[3], [32]。由于深度学习的进步，卷积神经网络最近被证明可以显著提高姿势估计的准确性和鲁棒性[27], [48], [62], [75], [76], 到目前为止，基于图像的六维姿势估计的重点是单一图像估计的准确性；大多数技术忽略了时间信息，只为物体的姿势提供了单一假设。然而，在机器人领域，时间数据和关于估计的不确定性的信息对于抓取计划或主动感应等任务也非常重要。视频数据中的时间跟踪可以改善姿势估计[7]、[10]、[31]、[46]。在基于点云的姿势估计方面，卡尔曼滤波也被用于跟踪6-D姿势，其中宾汉分布已被证明很适合于方向估计[59]。然而，单模态估计不足以充分代表由遮挡和可能的物体对称性引起的复杂不确定性。

在这篇文章中，我们介绍了一种基于粒子滤波器的方法来估计6维物体姿势的全部后验。我们的方法，称为PoseRBPF，将后验分解为物体的3-D平移和3-D旋转，并使用Rao-Blackwellized粒子过滤器，对物体姿势进行采样，并对每个粒子的旋转进行离散化分布估计。为了实现准确的估计，三维旋转是以5◦的分辨率离散的，导致每个粒子的分布在72×37×72=191 808个仓（海拔范围仅从-90◦到90◦）。为了实现实时性能，我们为所有离散的旋转预先计算了一个编码簿，其中嵌入来自一个自动编码器网络，该网络被训练为编码物体在一定比例下的任意视角的视觉外观（受[60]启发）。对于每个粒子，PoseRBPF首先使用3-D平移来确定图像中物体边界盒的中心和大小，然后使用自动编码器计算该边界盒的嵌入，最后通过使用余弦距离将嵌入向量与编码簿中预先计算的条目进行比较来更新旋转分布。每个粒子的权重是由旋转分布的归一化系数给出的。运动更新是通过对姿势的运动模型取样和对旋转的卷积来有效进行的。图1说明了我们用于6维物体姿势跟踪的PoseRBPF框架。在YCB-Video数据集[75]和T-Less数据集[24]上的实验表明，PoseRBPF能够表示由各种类型的物体对称性引起的不确定性，并能提供更准确的6维姿势估计。

图1. 用于六维物体姿势跟踪的PoseRBPF框架概述。我们的方法利用Rao-Blackwellized粒子过滤器和自动编码器网络来估计视频序列中目标物体的3-D平移和3-D旋转的完整分布。

我们的工作有以下主要贡献。

1. 我们引入了一个新的和通用的6-D物体姿势估计框架，该框架以一种高效和原则性的方式将Rao-Blackwellized粒子过滤与学习型自动编码器网络相结合。
2. 我们的框架能够跟踪基于RGB或RGB-D输入的6维物体姿势的全部分布。对于具有任意种类对称性的物体，它也能做到这一点，而不需要任何人工对称性标签。

与PoseRBPF[12]的上一版本相比，我们在本文中引入了以下改进。

1. 我们提出了一个受[17]启发的有效修改，我们应用兴趣区域（RoI）池来加速粒子评估。实验表明，在不牺牲跟踪精度的情况下，RGB-D跟踪速度可以提高68%以上。
2. 除了使用自动编码器对RGB测量进行编码外，我们还建议使用单独的自动编码器对深度测量进行编码，并表明跟踪性能可以得到显著提高。
3. 我们表明，我们的姿势估计框架可以与基于符号距离函数（SDF）的姿势精化模块相结合，以进一步提高姿势估计的准确性。
4. 我们表明，当物体检测不可用时，PoseRBPF可以通过在第一个视频帧上均匀采样粒子来初始化，然后在连续的帧上完善这一估计。
   本文的其余部分组织如下。在讨论了相关工作后，我们提出了用于6维物体姿势跟踪的Rao-Blackwellized粒子过滤框架，然后是实验评估和结论。

2. 相关工作

A. 六维物体姿态估计

我们的工作与最近使用深度神经网络进行六维物体姿势估计的进展密切相关。目前的趋势是用估计六维物体姿态的能力来增强最先进的二维物体检测网络。例如，Kehl等人[27]将SSD检测网络[40]扩展到6-D姿势估计中，将视角分类加入到该网络。Tekin等人[62]利用YOLO架构[51]检测图像中物体的3-D边界盒角，然后通过解决透视-n-点问题恢复6-D姿态。在[42]、[49]、[58]和[67]中也探讨了检测三维边框角或物体关键点来进行六维物体姿势估计。PoseCNN[75]基于VGG架构[57]设计了一个用于6-D物体姿势估计的端到端网络。尽管这些方法比传统方法[3], [21], [32]明显提高了六维姿态估计的准确性，但它们在处理对称物体时仍然面临困难，大多数方法都是手动指定每个此类物体的对称轴。为了处理对称物体，Tian等人[64]提出对旋转锚点进行均匀采样，并估计锚点与目标的偏差。此外，Sundermeyer等人[60], [61]通过训练一个用于图像重建的自动编码器，引入了一种隐含的表示三维旋转的方法，它不需要预先定义对称物体的对称轴。我们在工作中利用这种隐含的3-D旋转表示，并展示了如何将其与粒子过滤结合起来进行6-D物体姿态跟踪。

B. 六维物体姿态跟踪

另一组相关工作是关于视频中的物体追踪。早期的工作[6], [18], [68]利用图像特征（如边缘和关键点）追踪物体。然而，这些方法不能处理具有复杂纹理和闭塞的环境。它们在实际的机器人任务中是有限的。RGB-D传感器的引入大大简化了6-D姿势跟踪问题，因为场景的结构可以直接感知到颜色信息的赞美。使用RGB-D数据的物体跟踪得到了更多的关注[7]、[16]、[28]、[52]、[55]、[71]、[72]。尽管已经取得了重大进展，但由于深度传感器的限制，这些方法仍然不能在大规模或户外环境中稳健地工作，也不能用于小型或薄型物体。用RGB数据进行6-D姿势跟踪的最新进展包括[41]、[50]、[65]和[66]。在[50]中，物体的姿势是通过优化3-D模型的投影轮廓来更新的。该方法在[65]中通过一个新的优化方案和GPU并行化得到了改进。Tjaden等人[66]通过时间上一致的局部颜色直方图来改进姿势跟踪。同时，深度神经网络被探索用于6-D物体的姿势跟踪。最近，深度神经网络被用来预测连续帧之间的姿势差异，并相应地跟踪六维物体的姿势[36]，[41]，[72]。与使用手工制作的特征的方法相比，这些方法大大改善了跟踪的鲁棒性和准确性[50], [65], [66]。然而，在这些工作中，物体的对称性要么被忽略，要么被手动指定，并且需要6-D物体姿势估计来初始化跟踪管道。我们表明，我们的框架可以自动处理对称性，并且物体姿势跟踪可以只用2-D信息初始化，即第一个视频帧中物体的中心，甚至可以通过在图像中均匀采样颗粒来初始化，而不需要任何事先的空间信息。

C. 粒子滤波

粒子滤波框架在文献[29]、[45]、[54]、[56]中被广泛地应用于不同的跟踪应用，这要归功于它在纳入不同的观测模型和运动先验方面的灵活性。同时，它提供了一个严格的概率公式来估计跟踪结果的不确定性。人们还提出了不同的方法来使用粒子过滤器追踪物体的位置[2], [8], [35], [47], [74]。然而，为了达到良好的跟踪性能，粒子滤波器需要一个强大的观测模型。此外，跟踪帧率受到粒子采样和评估效率的限制。在这篇文章中，我们对6维物体姿态跟踪问题进行了因子化，并部署了Rao-Blackwellized粒子滤波器[15]，它已被证明可以扩展到复杂的估计问题，如同步定位和映射问题[44], [63]和多模型目标跟踪[34], [54]。我们还采用了一个深度神经网络作为观察模型，即使在闭塞和对称的情况下也能对物体的方向提供稳健的估计。我们的设计使我们能够使用高效的GPU实现来并行评估所有可能的方向。因此，我们的方法可以在20帧/秒的速度下跟踪物体的六维姿势分布。

3. 用PoseRBPF进行六维物体姿势跟踪

在这一节中，我们首先陈述了六维物体姿态跟踪的问题，并提供了PoseRBPF的高级概述。在用粒子滤波框架来表述这个问题之后，我们详细描述了如何利用深度神经网络来计算粒子的似然性，并实现高效的跟踪采样策略。

A. 问题定式化

给定到时间$k$的输入图像序列$Z_{1:k}$，对物体进行六维物体姿态跟踪的目标是估计图像流中每幅图像的相机坐标框架$C$和物体坐标框架$O$之间的刚体变换。我们假设第一幅图像中物体的二维中心$（u,v）$是由物体检测器提供的，如[17]和[51]中用于姿势跟踪的初始化，并且物体的三维计算机辅助设计（CAD）模型是已知的。刚体变换包括物体在时间$k$的三维旋转$R_k$和三维平移$T_k$。在本文中，我们的主要目标不是提供单一的估计$\{R_k，T_k\}$，而是估计物体的六维姿势的后验分布$P(R_k,T_k|Z_{1:k})$。

B. PoseRBPF概述

图2说明了我们的6维物体姿势跟踪框架的结构。PoseRBPF中的每个粒子都由一个平移假设和一个以平移假设为条件的旋转分布表示。在每个步骤中，粒子首先根据第三节E中描述的运动模型进行传播。每个粒子根据其平移确定一个独特的$RoI$，$RoI$被送入一个自动编码器网络以计算一个特征嵌入。观察似然是通过将嵌入与预先计算的编码簿中的嵌入相匹配来计算的，这将在第三节D中详述。最后，粒子的权重可以用观察似然来计算，粒子也相应地被重新采样。

图2. PoseRBPF的结构。对于每个粒子，旋转分布的估计以平移估计为条件，而平移估计则以相应的RoIs进行评估。

C. Rao–Blackwellized 粒子滤波器的公式

使用标准粒子滤波器[11], [63]对这个6维空间进行采样来估计后验分布$P(R_k,T_k|Z_{1:k})$是不可行的，特别是当物体的旋转存在很大的不确定性时。当物体被严重遮挡或具有导致多种有效旋转假说的对称性时，这种不确定性经常发生。因此，我们建议将6维姿势估计问题分解为3维旋转估计和3维平移估计。这个想法是基于这样的观察：3-D平移可以从图像中物体的位置和大小来估计。平移估计提供了图像中物体的中心和比例，在此基础上，可以从物体在边界框内的外观来估计三维旋转。具体来说，我们将后验分解为：

$$P(R_k,T_k|Z_{1:k})=P(T_k|Z_{1:k})P(R_k|T_k,Z_{1:k}),（1）$$

其中$P(T_k|Z_{1:k})$编码物体的位置和比例。而$P(R_k|T_k,Z_{1:k})$则是以平移和图像为条件的旋转分布模型。

这个因式分解直接导致了Rao-Blackwellized粒子滤波器的有效采样方案[15], [63]，其中时间$k$的后验由一组$N$个加权样本${\mathcal{X}}_k=\{T_k^i,P(R_k|T_k^i,Z_{1:k}),w_k^i{\}}_{i=1}^N$。这里，$T_k^i$表示第$i$个粒子的平移，$P(R_k|T_k^i,Z_{1:k})$表示以平移和图像为条件的粒子在物体旋转上的离散分布，而$w_k^i$是重要性权重。为了实现准确的姿势估计，由方位角、仰角和面内旋转组成的三维物体旋转被离散成大小为5◦的仓，从而使每个粒子在72×37×72=191 808个仓中分布（仰角范围仅从-90◦到90◦）。在每一个时间步骤$k$，粒子通过运动模型传播，产生一组新的粒子${\mathcal{X}}_{k+1}$，我们可以从中估计出6维姿势分布。

根据粒子过滤器的表述，$P(T_k|Z_{1:k})={\sum }_i{w}_k^i\delta (T_k-T_k^i)$，其中$\delta (\cdot )$代表零点的狄拉克三角函数。权重$w_k^i$可以被计算为

$$w_k^i\propto P(Z_k|T_k^i),（2）（w_k^i和P(Z_k|T_k^i)成正比）$$

$$=\int P(Z_k|T_k^i,R_k)P(R_k)d{R}_k,（3）$$

$$\approx \sum _{j}P(Z_k|T_k^i,R_k^j)P(R_k^j),（4）$$

其中$R_k^j$表示离散的旋转。

D. 观察似然

观测似然$P(Z_k|T_k,R_k)$衡量观测$Z_k$与物体姿势在三维旋转$R_k$和三维平移$T_k$下的兼容性。

直观地说，可以采用六维物体姿势估计方法，如[27]、[62]和[75]，来估计观测似然。然而，这些方法只提供6维姿势的单一估计，而不是估计概率分布，也就是说，它们的估计没有不确定性。此外，如果我们想在粒子过滤中评估大量的样本，这些方法的计算成本很高。

理想情况下，如果我们能在与观测值$Z_k$相同的场景中合成一幅具有姿态$（R_k，T_k）$的物体图像，我们就可以将合成图像与输入图像$Z_k$进行比较，以测量似然度。然而，这并不可行，因为要合成与输入视频帧中相同的光照、背景、甚至物体之间的遮挡物是非常困难的。相反，考虑到物体的三维模型，使用恒定的光照、空白背景和无遮挡来渲染物体的合成图像是很简单的。因此，受[60]的启发，我们应用一个自动编码器将观测值$Z_k$转化为与物体的合成渲染相同的域。然后，我们可以比较合成域中的图像特征，有效地测量6-D姿势的可能性。

1）自动编码器： 一个自动编码器被训练成将目标物体的姿态$（R，T）$的图像$Z$映射到由相同姿态渲染的物体的合成图像$Z^{\prime }$，其中合成图像$Z^{\prime }$是用恒定的照明渲染的，合成图像中没有背景和遮挡。通过这种方式，自动编码器被迫将具有不同照明、背景和遮挡的图像映射到共同的合成域。图3显示了训练期间自动编码器的输入和输出。此外，自动编码器还学习了输入图像的特征嵌入$f(Z)$。

图3. 自动编码器的输入和输出。具有不同照明、背景和遮挡的图像被送入网络，以便从相同的6-D姿势中重建物体的合成图像。编码器生成一个输入图像的特征嵌入（代码）。

我们没有训练自动编码器来重建具有任意6-D姿势的图像因为这使得训练具有挑战性，我们的做法是将3-D平移固定为一个典型的$T_0=(0,0,z{)}^T$，其中$z$是一个恒定的距离。典型的平移表示目标物体在摄像机的前面，距离为$z$。$z$可以通过优化三维模型到摄像机的距离来计算，这可以确保所有旋转的渲染与训练图像的大小（在我们的实验中为128×128）很好地匹配。三维旋转$R$在训练过程中是均匀采样的。训练结束后，对于每个离散的三维旋转$R^i$，使用编码器计算特征嵌入$f(Z(R^i,T_0))$，其中$Z(R^i,T_0)$表示目标物体从姿势$(R^i,T_0)$的渲染图像。我们认为离散的三维旋转的所有特征嵌入的集合是目标的编码本，接下来我们将展示如何使用编码本计算似然。

2）编码簿匹配： 给定一个三维平移假设$T_k$，我们可以从图像$Z_k$中裁剪出一个$RoI$，然后将$RoI$送入编码器，计算出$RoI$的特征嵌入。具体来说，三维平移$T_k=(x_k,y_k,z_k{)}^T$被投影到图像上，以找到$RoI$的中心$（u_k,v_k）$：

$$\left[\begin{array}{c}{u}_k\\ v_k\end{array}\right]=\left[\begin{array}{c}{f}_x\frac{x_k}{z_k}+p_x\\ f_y\frac{y_k}{z_k}+p_y\end{array}\right],（5）$$

其中$f_x$和$f_y$表示相机的焦距，$(p_x,p_y{)}^T$是主点。$RoI$的大小由$\frac{z_k}{z}s$决定，其中$z$和$s$分别是训练自动编码器时的典范距离和$RoI$大小。请注意，在我们的案例中，每个$RoI$是一个正方形区域，这使得$RoI$与物体的旋转无关。

$RoI$被送入编码器以计算特征嵌入$c=f(Z_k(T_k))$。最后，我们计算$RoI$的特征嵌入和编码本中的代码之间的余弦距离，这也被称为相似度得分，以衡量观察的可能性：

$$P(Z_k|T_k,R_c^j)=\varphi (\frac{c\cdot f(Z(R_c^j,T_0))}{||c||\cdot ||f(Z(R_c^j,T_0))||}),（6）$$

其中$R_c^j$是编码本中的一个离散旋转，$\varphi (\cdot )$是一个高斯概率密度函数，其中心是所有粒子的编码本中的最大余弦距离。图4说明了通过编码本匹配来计算旋转似然。通过这种方式，我们还可以根据贝叶斯规则获得给定平移的码本中所有旋转的概率似然分布，如下所示：

$$P(R_c^j|T_k,Z_k)\propto P(Z_k|T_k,R_c^j),（7）$$

图4. 通过编码簿匹配计算条件旋转似然。(左图）每个粒子根据其翻译假设对图像进行裁剪。每个粒子的RoI被调整大小，并使用编码器计算出相应的代码。(右图）旋转分布P(R|Z, T)是由每个假设的代码和编码本中的代码之间的距离计算出来的。

由于自动编码器是在物体位于图像中心和一定比例的情况下进行训练的，也就是说，在典型平移$T_0$的情况下，物体的任何比例变化或偏离图像中心的情况都会导致重建效果不佳（见图5）。具有不正确平移的粒子会产生物体不在$RoI$中心或具有错误比例的$RoI$。然后，我们可以检查$RoI$的重建质量来衡量平移假设的可能性。直观地说，如果平移$T_k$是正确的，那么（6）中接近地面真实旋转的旋转Ri的相似性分数会很高。最后，平移可能性$P(Z_k|T_k)$可按(4)计算。

从自动编码器重建RoI的可视化。左边是地面真实的RoI。其他两列显示了移位和比例变化后的重建。如图所示，重建的质量随着偏离地面真实RoI而下降。在这个例子中，相似度得分分别从0.91下降到0.62和0.72。这一特性使自动编码器成为计算观测似然的合适选择。

E. 运动先验

运动先验被用来传播从前一个时间步骤$k-1$到当前时间步骤$k$的姿势分布。我们使用一个恒定速度模型来传播3-D平移的概率分布。

$$P(T_k|T_{k-1},T_{k-2})=\mathcal{N}(T_{k-1}+\alpha (T_{k-1}-T_{k-2}),{\Sigma }_T),（8）$$

其中$\mathcal{N}（\mu ，\Sigma ）$表示均值为$\mu$、协方差矩阵为$\Sigma$的多变量正态分布，$\alpha$是恒定速度模型的超参数。旋转先验被定义为一个具有均值$R_{k-1}$和固定协方差${\Sigma }_R$的正态分布：

$$P(R_k|R_{k-1})=\mathcal{N}(R_{k-1},{\Sigma }_R),（9）$$

其中我们用欧拉角表示旋转$R$。然后，旋转先验可以通过对以前的旋转分布与三维高斯核的卷积来实现。

F. 6维对象姿态跟踪框架

追踪过程可以从任何输出目标物体的二维边界框的二维物体检测器中初始化。鉴于第一帧$Z_1$，我们对二维边界框的中心进行反投影，以计算三维平移的$（x，y）$分量，并对不同的$zs$进行均匀采样，以产生一组平移假设。具有最高可能性$P(Z_1|T)$的平移$T_1$被用作初始假设，$P(R|T_1,Z_1)$被用作初始旋转分布。

在接下来的每一帧，我们首先用运动先验来传播$N$个粒子。然后，用最新的观测值$Z_k$来更新粒子。具体来说，对于每个粒子，平移估计$T_k^i$被用来计算图像$Z_k$中物体的$RoI$。得到的$RoI$通过自动编码器来计算相应的代码。对于每个粒子，旋转分布被更新为：

$$P(R_k|T_k^i,Z_{1:k})=\eta P(R_k|T_k^i,Z_k)P(R_k|R_{k-1})P(R_{k-1})$$

其中，$P(R_k|T_k^i,Z_k)$是(7)中定义的旋转分布，$P(R_k|R_{k-1})$是运动先验，$\eta$是一个常数规范器。最后，我们根据（4）计算带有该粒子权重$w^i$的平移后验$P(T_k^i|Z_{1:k})$。系统重采样方法[14]被用来根据权重$w^{1:N}$对粒子进行重采样。

一些机器人任务需要从粒子滤波器中得到物体的六维姿势的期望值$(T_k^E,R_k^E)$用于决策。平移期望值T^E_k可以通过以下方式计算出来

$$T_k^E=\sum _{i=1}^N{w}_k^i{T}_k^i,（10）$$

由于物体跟踪任务中平移的单模态性质，所有$N$个粒子都是如此。计算旋转期望值$R_k^E$不太明显，因为分布$P(R_k)$可能是多模态的，简单地对所有离散的旋转进行加权平均是没有意义的。为了计算旋转期望值，我们首先计算旋转分布$P(R_k^E)$的期望值，用

$$P(R_k^E)=\sum _{i=1}^N{w}_k^{i}P(R_k|T_k^i,Z_{1:k}),（11）$$

然后，旋转期望值$R_k^E$是通过加权平均先前旋转期望值$R_{k-1}^E$的邻域内的离散自我中心旋转来计算的，使用的是[43]中提出的四元平均法。自我中心方向和分配中心方向之间的区别在[33]中描述。

用估计的RoI进行编码本匹配也提供了一种检测跟踪失败的方法。我们可以首先找到所有粒子之间的最大相似度得分。然后，如果最大分值低于预定的阈值，我们就把它确定为跟踪失败。算法1总结了我们用于6维物体姿势跟踪的Rao-Blackwellized粒子过滤器。

算法一

G. PoseRBPF的RGB-D扩展

PoseRBPF是一个通用的框架，可以在观察似然中用额外的深度测量来扩展。有了$RGB$输入$Z_k^C$和额外的深度测量$Z_k^D$，观察似然$P(Z_k|T_k,R_k)$可以重写为

$$P(Z_k|T_k,R_k)=P(Z_k^C,Z_k^D|T_k,R_k)=P(Z_k^C|T_k,R_k)P(Z_k^D|T_k,R_k),（12）$$

我们提出两种方法来计算深度测量的观察似然性$P(Z_k^D|T_k,R_k)$。在第一种方法中，可以根据每个粒子的旋转分布$P(R_k|T_k^i,Z_k^i)$中的平移$T_k^i$和最可能的旋转$R_k^{\ast }$渲染深度图。通过比较渲染的深度图和深度测量值，可以计算出深度的观测似然。在第二种方法中，深度测量值也可以用自动编码器进行编码，深度的观测似然可以通过类似于RGB图像的方式进行计算。除了用PoseRBPF进行过滤外，深度还可以用三维物体模型的SDF来进一步细化估计的姿势。

1. 渲染和比较：为了计算第i个粒子的可能性$P(Z_k^D|T_k^i,R_k)$，我们可以用姿势$(T_k^i,R_k^{\ast })$渲染物体，其中$R_k^{\ast }=argma{x}_{R_k}P(R_k|T_k^i,Z_k)$。为了比较渲染的深度图${\hat{Z}}_k^{Di}$和深度测量值$Z_k^D$，我们估计可见性掩码${\hat{V}}_k^i=\forall p,|{\hat{Z}}_k^{D_i}(p)-Z_k^D(p)|<m$，其中$p$表示图像中的一个像素，$m$是一个小的正常数保证金，以考虑传感器的噪音。因此，一个深度在$Z_k^D(p)\pm m$范围内的渲染像素$p$被确定为可见。有了估计的可见性掩码，两个深度图之间的可见深度差异被计算为

$${\Delta }_k^i({\hat{Z}}_k^{D_i},Z_k^D,{\hat{V}}_k^i,\tau )={\arg }_{p\in {\hat{V}}_k^i}\left(min\right(\frac{|Z_k^D(p)-{\hat{Z}}_k^{D_i}(p)|}{\tau },1\left)\right),（13）$$

其中$\tau$是一个预定的阈值。对于每一个粒子，我们计算它的深度分数为$s_d^i=v_k^i(1-{\Delta }_k^i)$，其中$v_k^i$是物体的可见度比率，即根据可见度掩码的可见像素数除以渲染的总像素数。最后，我们计算$P(Z_k^D|T_k^i,R_k)$为${\varphi }^{\prime }(s_d^i)$，其中${\varphi }^{\prime }(\cdot )$是一个高斯概率密度函数，其中心是所有粒子中的最大深度得分。

2. 对深度测量进行编码：另一种利用深度测量的方法是用一个单独的自动编码器网络计算观察似然$P(Z_k^D|T_k,R_k)$。对于每个粒子$\{T_k^i,P(R_k|T_k^i,Z_{1:k})\}$，我们首先将深度测量值归一化为

$${\overline{Z}}_k^D=f_c(\frac{Z_k^D-z_k^i}{d}+0.5),（14）$$

其中$d$是物体的直径，$z_k^i$代表物体的深度，$f_c(x)$是一个夹紧函数，定义为$f_c(x)=max(0,min(1,x))$。本质上，（14）根据粒子将深度测量归一化为[0，1]。我们在第四节中的实验表明，与编码原始深度值相比，归一化明显提高了跟踪精度。我们为归一化的深度训练一个单独的自动编码器，并以估计RGB图像的似然$P(Z_k^D|T_k,R_k)$的相同方式估计$P(Z_k^C|T_k,R_k)$ 。根据(12)，在粒子滤波框架中对观测似然进行融合。

3. 用SDFs进行姿态精化：来自PoseRBPF的估计物体姿势可以通过深度测量的三维点与目标物体的SDF相匹配来进一步完善。我们首先根据姿势期望值$（T_k^E,R_k^E）$渲染物体并与深度测量值进行比较来估计物体的分割掩码$\overline{V}$，如第III-G1节中所述。物体的点云$Pobj$可以通过反投影$\overline{V}$中的像素来计算。

$$P_{obj}=\{Z_k^D(p)K^{-1}{p}^{-T},p\in \overline{V}\},（15）$$

其中$K$代表相机的固有矩阵，$\overline{p}$代表像素$p$的同质坐标。

在计算出物体上的三维点后，我们通过将这些点与物体模型的SDF相匹配来优化姿势，如[55]。我们解决的优化问题是

$$(T^{\ast },R^{\ast })=\underset{T,R}{\mathrm{argmin}}\sum _{p_i\in P_{obj}}|SD{F}_{obj}(p_i,T,R)|,（16）$$

其中$p_i$是点云$P_{obj}$中的一个三维点，$SD{F}_{obj}(p_i,T,R)$表示通过使用姿势$(T,R)$将点$p_i$从相机坐标转换到物体模型坐标的有符号距离值。优化问题可以用基于梯度的方法以迭代的方式解决。在我们的方法中，解决方案以姿势期望值$（T_k^E,R_k^E）$初始化，并以亚当优化器[30]进行优化。

H. 快速PoseRBPF

受[17]的启发，我们提出了对PoseRBPF的修改，以加速对粒子的评估。据观察，在跟踪过程中，粒子的RoIs之间存在着明显的重叠。如图6所示，我们建议根据RoIs来裁剪来自编码器的特征图，而不是直接在输入图像上裁剪RoIs并为每个粒子单独传递它们，这样早期的卷积可以在粒子之间共享。我们把这种高效的变体称为快速PoseRBPF。

图6. 原始PoseRBPF和快速PoseRBPF中的自动编码器的比较。(a) 在原始PoseRBPF中，每个粒子直接在输入图像上裁剪其RoI并单独通过编码器。(b) 在快速PoseRBPF中，每个粒子在共享的特征图上裁剪，这样早期的卷积就可以在粒子之间共享。

具体来说，将粒子的平均平移表示为$\overline{T}=(\overline{x},\overline{y},\overline{z}{)}^T$，它在二维图像$(\overline{u},\overline{v}{)}^T$上的投影可以用（5）计算出来。我们首先以$(\overline{u},\overline{v}{)}^T$为中心对输入图像进行裁剪，尺寸为$\beta \frac{\overline{z}}{z}s$，其中$z$和$s$分别是训练自动编码器时的典型距离和尺寸，$\beta$是一个缩放系数，以确保裁剪后的图像足够大，能够覆盖粒子的所有$RoIs$。裁剪后的图像通过前三个卷积层来计算特征图。对于每个具有平移$T_k=(x_k,y_k,z_k{)}^T$和投影二维中心$(u_k,v_k{)}^T$的粒子，特征图上相应$RoI$的大小可以计算为$\frac{\overline{z}}{{\beta }_{z_k}}{s}_o$，其中$s_o$代表共享卷积层之后的特征图的大小。中心$（u_c，v_c）$可以计算为

$$(u_c,v_c)=(\frac{(u_k-\overline{u})\overline{z}}{z}\cdot \frac{s_o}{\beta s}+\frac{s_o}{2},\frac{(v_k-\overline{v})\overline{z}}{z}\cdot \frac{s_o}{\beta s}+\frac{s_o}{2})$$

用[19]中提出的RoI对齐操作对特征图进行裁剪，并将裁剪后的特征分别送入以下网络层以生成粒子的代码。

4. 实验

A. 实施细节

1) 网络结构： RGB输入的自动编码器与[60]中的编码器相同。它接收大小为128×128的图像，由四个5×5卷积层和四个5×5解卷积层组成，分别用于编码器和解码器。在卷积层之后，一个全连接层被用来产生128-D嵌入。我们使用类似的结构，但在深度自动编码器中把卷积层的通道数减少一半，以避免过度拟合。对于Fast PoseRBPF，缩放系数β被设置为2。因此，用于生成特征图的输入图像的大小为256×256。粒子共享前三层的卷积运算；因此，也是32。

2) 训练： RGB-D训练数据是纯粹的合成数据，通过根据给定的CAD模型以随机旋转的方式渲染一个物体而产生。渲染的图像是在MS-COCO数据集[38]的随机裁剪处叠加的，分辨率为128×128。首先根据（14）对深度数据进行归一化，d=0.4。归一化深度的背景数据是通过对MS-COCO数据集中随机作物的RGB通道进行平均而产生的。除了目标物体外，另外三个物体以随机的位置和比例取样，以产生有遮挡物的训练数据。目标物体被定位在图像的中心，并以5个像素进行抖动。该物体在0.975和1.025之间的尺度上被均匀采样，并有随机照明。颜色在色相、饱和度、数值（HSV）空间中随机化。我们还在RGB和归一化深度中分别加入标准偏差为0.1和0.5的高斯噪声，以减少真实数据和合成数据之间的差距。每个训练步骤的图像都是在线渲染的，以提供更多样化的训练数据集。

使用学习率为0.0002的Adam优化器，对每个物体分别进行150 000次迭代的自动编码器训练，批量大小为64。自动编码器在具有最大重建误差的N个像素上用L2损失进行优化。较大的N更适合于纹理物体，以捕捉更多的细节。我们对有纹理的物体使用N=2000，对没有纹理的物体使用N=1000。

3）测试： 在测试时间内，用于计算(6)中观察可能性的标准差为0.05。每个物体的编码本都是离线预计算的，并在测试时间内加载。观察似然的计算在GPU上有效进行。在深度输入方面，对于III-G节中描述的渲染和比较方法，在我们的实现中，余量$m$被选择为2厘米，阈值$\tau$被设置为3厘米。$\varphi (\cdot )$的标准偏差被设定为0.05。由于为每个粒子渲染单独的深度图可能很昂贵，而渲染和比较方法的主要目标是改善平移估计，在我们的实现中，我们在跟踪过程中为所有粒子渲染最可能的姿势的深度图；然后，渲染的深度图通过补偿用于渲染的平移和每个粒子的平移之间的差异来调整。对于初始化，深度图是为每个粒子单独渲染的。为了用SDF完善姿势估计，我们将Adam优化器的学习率设置为0.01，并将优化器运行100步。我们在一台装有英特尔i7 CPU和英伟达TitanXp GPU的台式电脑上进行实验。

B. 数据集

我们在两个六维物体姿态估计的数据集上评估我们的方法：T-LESS数据集[24]和YCB视频数据集[75]。T-LESS数据集包含30个无纹理工业物体的RGB-D序列。评估是在20个测试场景中进行的。T-LESS数据集具有挑战性，因为这些物体没有纹理，而且有各种形式的对称性和遮挡。YCB视频数据集包含来自YCB物体和模型集的21个物体的RGB-D视频序列[4]。它包含不同排列方式的有纹理和无纹理的家庭物体。在这两个数据集中，物体都有6维姿势的注释。

C. 评估指标

对于T-LESS数据集，我们使用可见表面差异$er{r}_{vsd}$[23]来评估姿势估计的质量。它的计算方法是

$$er{r}_{vsd}=av{g}_{p\in \hat{V}\cup V_{gt}}c(p,\hat{D},D_{gt},\tau )$$

$$c(p,\hat{D},D_{gt},\tau )=\{\begin{array}{rlr}d/\tau & ,& ifp\in \hat{V}\cap V_{gt}\wedge d<\tau \\ 1& ,& otherwise\end{array}$$

其中，$\hat{V}$、$\hat{D}$和$V_{gt}$、$D_{gt}$分别代表根据估计姿势和地面真实姿势渲染物体而计算出的物体的掩模和深度图；$p$代表图像中的一个像素；$d$是深度误差，可以用$d=|\hat{D}(p)-D_{gt}(p)|$来计算；$\tau$是一个常数公差。我们报告了正确的6-D姿势的召回率，其中$er{r}_{vsd}<0.3$，$\tau =2cm$，可见度超过10%，遵循[22]。

对于YCB视频数据集，我们使用ADD和ADD-S[21], [75]作为评价指标。这两个指标可以被计算为
$$ADD=\frac{1}{m}\sum _{x\in \mathcal{M}}||(Rx+T)-(Rx+T)||$$

$$ADD-S=\frac{1}{m}\sum _{x_1\in \mathcal{M}}mi{n}_{x_2\in \mathcal{M}}||(R{x}_1+T)-(R{x}_2+T)||$$

其中$\mathcal{M}$表示三维模型点的集合，$m$是点的数量。$(R,T)$和$(R,T)$分别是地面真实姿态和估计姿态。

D. 消融研究

我们在T-LESS数据集上进行消融研究，以证明我们的设计选择。粒子过滤器以RetinaNet[39]的检测输出为初始化，有100个粒子。表一显示了消融研究的结果。

表一

1) 原始PoseRBPF与快速PoseRBPF： 第1-4行显示了原始PoseRBPF与快速PoseRBPF的比较。结果显示，快速PoseRBPF结构明显提高了跟踪速度，对于RGB来说提高了70%，对于RGB-D来说提高了93%。对于RGB输入的6维物体姿势跟踪精度，原始PoseRBPF明显优于快速PoseRBPF（第1行和第2行）。这种性能差距并不奇怪，因为卷积操作后空间分辨率下降，对特征空间的裁剪将导致平移估计的准确性降低。然而，性能差距是通过深度测量来弥补的（第3行和第4行），因为根据粒子渲染物体并与深度测量进行比较，可以更准确地估计平移。因此，我们只将快速架构用于RGB-D追踪，以保持RGB追踪的准确性。

2) 渲染和比较： 通过比较第1行和第3行，可以看出利用深度测量的好处和提议的渲染和比较策略的有效性。通过包括深度输入，可以更好地估计观测似然，并实现更准确的6-D姿势估计。

3）深度嵌入： 我们首先调查了对深度测量进行编码是否有助于提高跟踪的准确性。第2行和第5行显示，对深度测量进行编码可以提高追踪的准确性，提高幅度超过100%。尽管对深度测量进行编码的改善没有渲染和比较策略那么明显（第4行），但这两种方法可以一起利用，以进一步提高跟踪精度（第7行）。深度自动编码器可以被天真地训练来编码原始的深度测量值，这些测量值是公制的。然而，通过比较第6行和第7行，包括原始深度的自动编码器在内的跟踪性能明显恶化了。这种负面影响是由原始深度的大方差造成的，它证明了在将深度输入自动编码器之前用（14）对深度进行归一化。

4) RGB和深度融合： 除了深度表示，我们还研究了不同的方法来融合RGB和深度测量。一个直接的方法是用一个额外的深度通道来增强RGB输入的自动编码器。在这种情况下，深度测量与自动编码器中的RGB输入相融合，这被称为早期融合，与III-G节中提出的融合粒子过滤器中的观测似然（后期融合）相反。通过比较第7行和第8行，我们可以看到，晚期融合的结构比早期融合的结构实现了更好的准确性。这是因为粒子滤波器在贝叶斯估计框架中平衡了不同的模式，而从合成数据中很难学到相对重要性。通过比较第7行和第10行，可以看出，将RGB和深度输入融合在一起，比单独使用深度信息可以得到明显更准确的姿势跟踪。

5) 姿势精化： 从第7行和第9行也可以看出，姿势估计可以通过优化SDF来进一步完善，如第III-G节所述。

E. 在T-LESS数据集上的结果

表二将我们的方法与其他几种方法在T-LESS数据集上进行了比较。我们使用100个粒子来跟踪物体。对于RGB输入的姿势估计，我们将我们的方法与[60]进行了比较，后者使用了类似的自动编码器。然而，平移和方向是单独估计的，而且[60]中没有利用时间上的一致性。我们用[60]中使用的RetinaNet[39]的检测输出进行了评估。当检测到样本物体的多个实例时，我们使用列表中的第一个实例进行初始化。结果表明，通过在粒子过滤器中联合估计平移和方向并考虑时间一致性，正确物体姿势的召回率增加了一倍。有了额外的深度图像，召回率可以进一步提高到98%左右。我们在这里使用带有编码深度的Fast PoseRBPF进行比较。在没有细化的情况下，我们的方法比使用迭代最接近点（ICPs）的[60]要好41%，比[26]好124%，比[69]好21%。通过细化，我们的方法比使用ICP的细化[60]好45%，[26]好130%，[69]好25%。对于使用地面真实边界框的实验，旋转是使用粒子过滤器跟踪的，而则是根据地面真实边界框的比例推断出来的。这个实验突出了视角的准确性。在这种情况下，粒子过滤器的性能明显优于[60]和[1]，这表明时间跟踪对物体姿势估计的重要性。图7显示了PoseRBPF在几张T-LESS图像上的6维姿势估计。

表二

F. 在YCB视频数据集上的结果

表三和表四显示了对YCB视频数据集的姿势估计结果。在表三中，我们与最先进的基于单视图的6维物体姿势估计方法进行了比较，该方法使用RGB图像[36], [75]和RGB-D图像[36], [70], [75] 。图7说明了在YCB视频数据集上估计6-D姿势的一些例子。我们使用PoseCNN检测[75]在第一帧或物体被严重遮挡后初始化PoseRBPF。平均而言，每个序列只发生了1.03次。在实验中，100个粒子被用来跟踪6-D姿势。对于RGB输入的跟踪，我们的方法处理对称物体，如024_bowl, 061_foam_brick，比直接回归方向的方法好得多[75]。通过对来自PoseCNN的姿势进行进一步的基于图像的细化，DeepIM[36]实现了比我们的方法更准确的六维姿势估计。

图7. T-LESS数据集（前两行）和YCB视频数据集（最后两行）上的估计姿势的可视化。地面真相的边界框为红色，绿色边界框为粒子RoI，物体模型在PoseRBPF估计的姿势下叠加在图像上。

表三

表四

在机器人定位的背景下，已经证明了增加根据最近的观察结果绘制的样本可以提高定位性能[63]。在这里，我们应用了这样一种技术，围绕PoseCNN的预测对50%的粒子进行采样，另外50%则使用运动模型。我们的结果表明，这样的混合版本（Ours++）提高了我们方法的姿势估计精度，这要归功于更精确的提议分布。PoseRBPF表现不佳的对象之一是木块，这是由于木块的三维模型的纹理和真实图像中使用的木块的纹理不同造成的。此外，木块的物理尺寸在真实图像和本数据集中包含的模型之间是不同的。

如T-LESS数据集的结果所示，深度测量包含有用的信息来提高姿势估计的准确性。这种改进在YCB视频数据集上是一致的。还值得注意的是，深度测量也有助于弥合合成训练数据和真实测试数据之间的差距，从而使木块等物体的跟踪性能大大改善。通过比较渲染物体的深度与深度测量和编码深度测量，我们的过滤方法比[75]的ICP和融合方法[70]取得了更好的准确性。通过与SDF的细化，精度可以进一步提高，我们的方法达到了最先进的性能。

在表四中，我们将我们的方法与6-D物体姿势跟踪方法进行比较。我们首先将PoseRBPF与使用标准粒子滤波器的六维物体姿势跟踪基线进行比较。在这个基线中，每个粒子用一个平移假设$T_k^i$和一个旋转假设$R_k^i$表示，我们相应地渲染RGB图像${\hat{Z}}_k^{C_i}$、深度图像${\hat{Z}}_k^{D_i}$和物体的掩码${\hat{M}}_k^i$。假设物体$M_k$的分割掩码已经给出。我们可以计算出平均光度误差${\Delta }_k^{C_i}$和深度误差${\Delta }_k^{D_i}$为

$${\Delta }_k^{C_i}=av{g}_{p\in ({\hat{M}}_k^i\cap M_k)}(|{\hat{Z}}_k^{C_i}(p)-Z_k^C(p)|)$$

$${\Delta }_k^{D_i}=av{g}_{p\in ({\hat{M}}_k^i\cap M_k)}(|{\hat{Z}}_k^{D_i}(p)-Z_k^D(p)|)$$

我们也可以计算估计的分割掩码${\hat{M}}_k^i$和测量的分割掩码$M_k$之间的交集和联合的比率，并将其记为$m_k^i$。RGB和RGB-D跟踪的观察似然可以计算为

$$P_{RGB}(Z_k|T_k^i,R_k^i)={\varphi }_c({\Delta }_k^{C_i}){\varphi }_m(m_k^i)$$

$$P_{RGB}(Z_k|T_k^i,R_k^i)={\varphi }_c({\Delta }_k^{C_i}){\varphi }_d({\Delta }_k^{D_i}){\varphi }_m(m_k^i)$$

其中${\varphi }_c(\cdot )$和${\varphi }_d(\cdot )$是以0为中心的高斯函数，${\varphi }_m(\cdot )$是以1为中心的高斯函数。在实验中，我们使用基线中的地面真相分割掩码和100个粒子。如表四所示，在RGB和RGB-D场景中，PoseRBPF的表现明显优于使用标准粒子过滤器的基线。这些比较证明了PoseRBPF在6-D姿势跟踪中比标准粒子过滤器有更高的采样效率，以及学习到的自动编码器网络在处理输入图像的光照差异和噪声时提供的鲁棒性。

此外，我们将我们的方法与其他6-D物体姿势跟踪方法[25], [36], [72], [73]进行了比较。在RGB-D追踪方面，我们的方法取得了与最近最先进的方法[72]相当的精确度。对于基于RGB的跟踪，我们的方法不如基于细化的方法（如[36]）准确。与现有的六维物体姿态跟踪系统相比，我们的方法仍然提供了一个有用的选择，因为我们的方法跟踪完整的六维姿态分布，并且只需要二维检测中心进行初始化，而不是像DeepIM[36]那样需要初始化六维姿态估计。

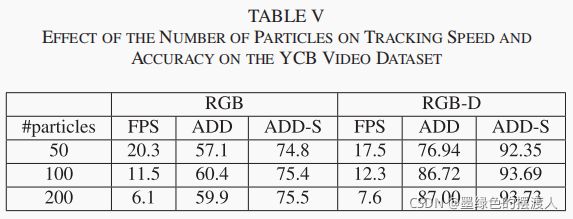
表五显示了颗粒数量对跟踪速度和精度的影响。当粒子数较少时，随着粒子数的增加，精确度会提高，因为有了更多的样本，物体的尺度和平移的变化会被覆盖得更好。然而，我们也可以观察到，跟踪性能在100个粒子之后就会饱和，100个粒子的性能与200个粒子的性能相似。

表五

G. 旋转分布的分析

与其他6-D姿势估计方法不同的是，PoseRBPF对物体的3-D旋转输出单一的估计值，PoseRBPF跟踪物体旋转的全部分布。图8显示了旋转的例子分布。这些分布中有两类不确定因素。第一个来源是物体的对称性导致了具有类似外观的多个姿势。正如预期的那样，每个视点的集群都对应于一个相似性模式。每个集群的方差对应于姿势的真实不确定性。例如，对于碗来说，每个旋转环对应于方位角的不确定性，因为碗是一个旋转对称的物体。不同的环显示了仰角上的不确定性。

图8. 旋转分布的可视化。对于每幅图像，旋转的分布是可视化的。线条代表高于阈值的旋转的概率。每条线的长度与该视点的概率成正比。可以看出，PoseRBPF自然地表示了由于各种对称性造成的不确定性，包括碗的旋转对称性和T-LESS物体的镜像对称性12。

为了衡量PoseRBPF对旋转不确定性的把握程度，我们将PoseRBPF的估计值与PoseCNN的估计值进行了比较，假设高斯不确定性的平均值为PoseCNN的估计值。图9显示了YCB视频数据集中的剪刀和泡沫砖的这种比较。这里，X轴的范围是旋转分布的百分位数，Y轴显示了地面真实姿势在相应百分位数所包含的一个旋转的0◦、10◦或20◦之内的频率。例如，对于剪刀，红色实线表示80%的时间里，地面真实的旋转是在PoseRBPF分布的前20%的旋转的20◦以内。如果我们采取PoseCNN估计的前20%的旋转，假设有高斯不确定性，这个数字会下降到60%左右，如下面的虚线、红线所示。对于具有180◦对称性的泡沫砖，保持多模态不确定性的重要性变得更加突出。在这里，PoseRBPF实现了高覆盖率，而PoseCNN则未能产生良好的旋转估计值，即使在进一步远离生成的估计值时也是如此。

图9. PoseRBPF和PoseCNN对剪刀和泡沫砖的旋转覆盖率比较。泡沫砖有180◦的平面旋转，而剪刀是一个不对称的物体。

H. 全局定位

在前面的讨论中，我们重点讨论了物体姿势跟踪，其中PoseRBPF是由二维检测框架初始化的，如[39]和[75]。然而，没有概念上的理由说明为什么PoseRBPF不能被部署到全局姿势估计中，从而克服了对检测框架的需求。在此，我们提出一种基于全局采样的方法来初始化系统。我们首先通过对图像中物体的二维中心p进行均匀采样，对物体的距离在$[Z_k^D(p)-0.1,Z_k^D(p)+0.2]$中进行均匀采样。我们评估2400个样本，找到最可能的一个，并在其周围以细粒度的方式取样100个粒子：对于图像中的物体中心和距离，我们分别用标准偏差为5像素和0.015米的高斯函数取样。当所有粒子之间的最大相似性分数大于阈值（0.6）时，我们开始跟踪该物体；否则，我们重复全局定位过程。我们在图10中直观地展示了全局定位过程、成功的初始化例子和失败的案例。我们在YCB视频数据集上评估了全局定位策略。利用所提出的全局定位策略，我们的跟踪系统可以在YCB视频数据集中所有物体的55个测试序列中的49个中成功初始化，其结果是ADD为83.45，ADD-S为89.06。在我们的实验中，我们观察到初始化失败发生在物体的深度测量缺失（金枪鱼罐头），或者物体被严重遮挡（布丁盒），或者物体的纹理与模型有明显不同（木块）。

图10. YCB视频数据集上的全局定位的可视化。(a) 全局定位过程。我们在平移空间中均匀地对粒子进行采样。在评估了所有的粒子后，我们在具有最大权重的粒子周围进行细粒度的采样。当所有粒子之间的最大相似性分数高于阈值时，跟踪过程被触发。(b) 成功的初始化。(c) 失败的情况。

5. 结论

在这篇文章中，我们介绍了PoseRBPF，一个用于跟踪6维物体姿势的Rao-Blackwellized粒子过滤器。每个粒子对3-D平移进行采样，并估计3-D旋转的分布，其条件是对应于采样平移的图像绑定盒。PoseRBPF将每个绑定盒嵌入与学习到的观点嵌入进行比较，以便随着时间的推移有效更新分布。我们证明了跟踪的分布既能捕捉到物体对称性的不确定性，又能捕捉到物体姿势的不确定性。在两个基准数据集上的实验表明，PoseRBPF有效地估计了家用物体和无对称纹理的工业物体的6维姿势。

PoseRBPF有几个局限性，有待解决。当物体被严重遮挡或测量结果与合成训练数据有明显差异时，PoseRBPF会失败。图11说明了在YCB视频数据集中由于遮挡而导致的跟踪失败。我们显示了物体被遮挡的比率和所有粒子的最大相似度得分。可以看出，最大相似度随着闭塞度的增加而降低。在这个例子中，当最大相似度低于0.6时，系统就会判定失败，这相当于65%的物体被遮挡。处理遮挡问题的一个潜在方法是用视觉测距法更准确地估计摄像机的运动，这样粒子过滤器对观测更新的依赖就会减少。用真实的注释数据对神经网络进行微调，可以有效地弥补合成训练数据和真实测试测量之间的领域差距，这也促使我们以自我监督的方式注释真实数据的工作[13]。另一个限制是，每个对象都需要它自己的自动编码器。为多个不同的物体训练一个自动编码器是值得探索的。此外，通过用连续函数表示旋转分布来改进方向估计是值得研究的。

由于闭塞导致的跟踪失败的例子。该图显示，最大相似度（蓝色曲线）随着闭塞度（红色曲线）的增加而降低。在我们的实现中，当最大相似度低于0.6时，系统就会确定追踪失败。因此，在这个例子中，我们的系统可以在失败之前处理大约65%的遮挡。