论文笔记（三十八）HandyPriors: Physically Consistent Perception of Hand-Object ... Differentiable Priors

文章概括

作者：Shutong Zhang, Yi-Ling Qiao2, Guanglei Zhu1, Eric Heiden, Dylan Turpin, Jingzhou Liu, Ming Lin, Miles Macklin, Animesh Garg
来源：arXiv:2311.16552v2 [cs.CV] 3 Dec 2023
原文：https://arxiv.org/pdf/2311.16552.pdf
代码、数据和视频：
系列文章目录：
上一篇：
https://blog.csdn.net/xzs1210652636/article/details/134431873
下一篇：

摘要

在过去的工作中，人们提出了各种用于模拟手-物交互的启发式目标。然而，由于缺乏一个连贯的框架，这些目标的适用范围往往很窄，效率或准确性也受到限制。在本文中，我们提出了 “HANDYPRIORS”，这是一个统一的通用管道，可利用可微分物理和渲染领域的最新进展，对人机交互场景进行姿势估计。我们的方法利用渲染先验与输入图像和分割掩码保持一致，同时利用物理先验减轻穿透和跨帧相对滑动。此外，我们还提出了手部和物体姿态估计的两种替代方案。基于优化的姿态估计精度更高，而基于滤波的跟踪利用可微分先验作为动态和观测模型，执行速度更快。我们证明，HANDYPRIORS 在姿态估计任务中取得了相当或更优的结果，而且可微物理模块可以预测用于姿态细化的接触信息。我们还证明，我们的方法适用于感知任务，包括机器人手部操作和在野外，人-物姿势估计。

1. 介绍

手是人类与物理世界交互的主要工具，因为大部分复杂而灵巧的物体操作任务都是由手完成的。充分了解手与物体的交互有助于完成许多基于学习的任务，如动作识别[1]、机器人操纵[2]、用户交互[3]等。

估算手与物体的交互作用是一项挑战。首先，手部复杂、可变形的几何形状和动态特性给学习和优化带来了挑战。与刚性物体不同，手是用关节铰接的，具有很高的自由度。它们的非线性和非凸性进一步加剧了任务的复杂性。其次，由于存在自我遮挡和手与物体之间的遮挡，因此在操作过程中预测手的姿势时存在不确定性。最后，在交互场景中，手与物体之间的接触非常丰富，因此需要对手和物体采用一致的估计方法，以避免穿透。

估计手和物体姿势的方法通常分为两类。第一种方法纯粹基于学习，即精心设计网络架构、损失函数和训练策略，以训练从图像到手和物体配置的通用映射[4], [5]。虽然神经网络和大型训练数据集可以减轻高自由度和非凸性带来的困难，但它们不能保证可解释性或正确性。第二类方法是基于优化的方法[6]、[7]，包括定义和优化启发式目标函数，以提高物理可行性和减少穿透。虽然优化过程可能较慢，但每帧迭代可以提高结果的准确性。

在本文中，我们利用了学习和优化技术。我们的方法利用预先训练好的网络来提供姿势的初始估计值，然后使用可微分的自监督项，通过纠正像素级错位和非物理穿透/振荡造成的误差来进一步完善估计值。受大规模视觉和语言模型自监督学习成功经验的启发[8], [9]，我们采用类似的技术来估计手与物体之间的交互。具体来说，我们建议通过与后续视频帧进行比较来监督姿势预测，这与使用序列补全训练文本生成的方式类似。

为了实现图像空间梯度的反向传播，我们开发了完全可变的算子，用于模拟和渲染预测的姿势。这种闭环优化方法使估计结果与输入图像更加相似，从而提高了准确性。我们还加入了几个正则化项，以尽量减少预测序列中的运动振荡和碰撞。

虽然优化过程可以提高精度，但却非常耗时。为了解决这个问题，我们提出了一种基于卡尔曼滤波器[10]的替代滤波技术，以进一步利用我们的可微分动力学和观测模块。这种方法允许用户在效率和精度之间做出权衡，具体取决于他们是选择执行在线跟踪还是离线优化。利用这一集成的可微分渲染和模拟管道，我们还将姿势估计方法应用于人类和合成机器人手部场景，证明了我们方法的通用性和鲁棒性。图 1 总结了这种方法的几种应用。

图 1：HANDYPRIORS 是一个可用于多种任务的模块化程序块。可以通过（a）基于优化的细化或（e）使用扩展卡尔曼滤波器（EKF）进行滤波来实现手与物体交互的估计。此外，可变接触模块还可用于根据接触状态进行(b)姿势细化。我们的可微分先验也可用于(c)机器人手或(d)人体场景的姿态估计。

总之，这项工作的主要贡献是：

• 综合可变渲染（III-B 节）和模拟（III-C 节）管道，估算手与物体之间的交互作用。
• 离线优化（第 III-D 节）和在线跟踪（第 III-E 节）流程可以预测姿势和联系信息，为用户提供在准确性和效率之间取得平衡的选择。
• 将我们的先验推广到各种应用的实验，例如机器人操纵（第 IV-A 节）、接触细化（第 IV-D 节）和人体（第 IV-E 节）。

在我们的实验中，我们的方法在手-物体-交互数据集 [11], [12] 中取得了相当或更好的姿态估计结果。此外，我们还证明，我们的方法所预测的接触信息能有效完善姿势估计。我们的消融研究比较了优化和跟踪结果之间的差异，进一步验证了不同损失的贡献。

2. 相关工作

从单目图像[13]、[14]、[15]、[16] 中估计手和物体的姿态是计算机视觉中的一个基本问题。最近的许多研究都是假设已知的刚性网格模型来预测 6 DoF 物体姿态 [17]、[18]、[19]。对于人手，MANO[20] 提出了一个参数模型，使用不同的形状和姿势参数来表示手的几何形状。许多基于学习的方法侧重于从 RGB(D) 输入预测 3D 关节位置 [21]、[22]、[23]、[24]、[25]、[26]、[27]。其他方法 [28]、[29]、[7]、[30] 则根据 MANO 姿态和形状参数进行回归。还有一些方法直接从注释数据集中学习视觉输入和手部姿势之间的映射[31], [32], [33], [34]。这些方法在只有手的数据集上取得了显著的成功，但在手拿物体时表现不佳。还有一些基于优化的方法，可根据二维关键点[6]、[7]、[35]或分割[11]优化手部参数。它们往往具有更高的精度，但由于迭代优化过程，速度要慢得多。我们提出的基于跟踪的管道具有更高的效率。我们的可微分先验更加通用，可应用于更广泛的领域。

手与物体的交互越来越受到关注。将手和物体的姿势估计分开处理会导致两者的估计都不准确。随着越来越多的手与物体数据集被创建出来 [36], [37], [38], [11], [4], [39]，最近的许多研究开始关注手与物体的联合跟踪。然而，由于遮挡和深度模糊性，同时估算两者具有挑战性。[5] 设计了一个基于手和物体表征之间上下文推理的联合学习框架。[40] 提出了一种顺序关系损失来纠正手和物体之间的深度错位。文献[41]采用了一种特征注入机制，通过将手部信息整合到遮挡区域来更好地处理遮挡问题。这些方法提高了姿势估计的准确性，但却很少关注手与物体之间的物理交互。其他作品旨在预测物理上可信的手部物体姿势。为了实现这一目标，交互约束被应用于鼓励接触和最小化相互渗透。[7]、[6] 提出使用符号距离函数（SDF）来模拟手与物体之间的接触，[42] 设计了一个深度网络来估计接触面积，并使用虚拟胶囊技术来模拟手部软组织变形。[43]应用运动和力矢量来重建交互。与这些方法相比，我们的方法更具通用性，可用于人手和非人手场景中基于接触的细化和姿势估计。

可微分优先级。 可微分渲染 [44], [45], [46] 和物理 [47], [48], [49] 已被用于解决逆问题，以提高优化效率。对于手的抓取，[50] 利用物理模拟器来评估手与物体之间的动态交互。[51]、[52] 利用可微分物理学来生成物理上真实和稳定的抓取。最近还有一些作品利用可变渲染来优化人类 [53] 或物体 [54] 的姿势。不过，这些作品并没有考虑它们之间的物理交互。例如，[55] 利用可微分关节体模拟器来学习和平滑人体姿态估计。相比之下，我们的方法利用了每一帧的渲染先验，从而大大加快了视频中的姿势估计。

3. 方法：HANDYPRIORS

A. 问题设置

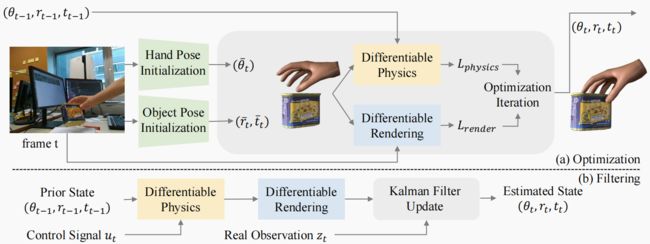
给定一系列 RGB 手-物体-交互图像和物体的 3D 模型，我们提出了两个管道来估计每帧图像中手和物体的配置。图 2 显示了我们的方法概览。

图 2：我们的优化和过滤管道概览。我们提供了两种利用可微分先验的方案。给定图像和之前帧的估计值后，(a) 优化管道首先使用预先训练好的网络初始化姿势，然后最小化可微分算子带来的渲染和物理损失；(b) 过滤管道可以使用一些简单的观察结果，并使用扩展卡尔曼滤波器（EKF）更新状态估计值。EKF 需要可微分物理和渲染来为系统建模，运行速度比优化管道快得多。

具体而言，我们使用 MANO [20] 参数化来表示手部，该参数化通过手部姿态 $\theta \in {\mathbb{R}}^{45+6}$ （表示 15 个手部关节的旋转和 6 DoF 全局变换）和形状 $\beta \in {\mathbb{R}}^{10}$ （统计模型）参数来描述手部。手部网格的 778 个顶点 ${\mathbf{V}}_{hand}\in {\mathbb{R}}^{778\times 3}$ 可以通过学习的线性模型 ${\mathbf{V}}_{hand}=m(\theta ,\beta )$ 根据 $\theta 、\beta$ 计算得出。

物体姿态有 6 个自由度，包括平移 $\mathbf{t}\in R^3$ 和旋转（用 $\mathbf{XYZ}$ 欧拉角表示）$\mathbf{r}\in R^3$。

B. 可变渲染先验

我们方法的第一个先验是可微分渲染，它有助于将估计的三维模型与二维图像对齐。实例分割是我们优化手部和物体姿势所依赖的关键信息。我们使用在 COCO 数据集 [57] 上训练的分割检测器 [56] 来提取手部和物体遮罩。我们的实验表明，虽然图像分割检测器 PointRend [56] 没有在 YCB 对象 [58] 上经过训练，但它可以正确预测对象掩码。但是，由于指尖较难检测，它无法充分分割手部。因此，我们进一步对 PointRend 进行了训练，以获得更好的手部和手持物体分割效果。

对于每一帧，我们使用可微分渲染器 SoftRas [44]，将三维手部和物体模型光栅化并投影到二维，然后通过将投影顶点拟合到手部和物体遮罩上，优化手部参数 $\theta$ 和物体参数 $\mathbf{r},\mathbf{t}$。接下来，我们将描述与渲染部分相关的损失项。

RGB 图像损失。 由于手部纹理因人而异，我们只渲染物体的 RGB 图像。然后，我们在渲染图像 $I_r$ 和经检测到的物体遮罩 $M_{obj}$ 裁剪的输入 RGB 图像 $I_{in}$ 之间应用 L2 损失。图像损失项可表示如下：
$$L_{img}(\mathbf{r},\mathbf{t})=\Vert (1-M_{hand})I_r-M_{obj}{I}_{in}{\Vert }_2^2\text{\hspace{1em}(2)}$$

遮罩损耗。 与 RGB 图像损耗相比，掩码的特征较少，但对光照和纹理不敏感，因此基于掩码的损耗更加稳健和通用。我们使用可微分渲染器来渲染手和物体的轮廓。然后，我们在渲染的遮罩 $M_r$ 和检测到的遮罩 $M_d$ 之间应用 L2 损失、

$$L_{mask}(\theta ,\mathbf{r},\mathbf{t})=\Vert M_r-M_d{\Vert }_2^2\text{\hspace{1em}(2)}$$

C. 可微物理先验

除了在二维图像空间中定义的渲染先验，我们还在三维和时间域中添加了更多与物理相关的先验，以帮助我们规范手部物体的理解。

接触损失。 在操作过程中，我们观察到手和物体之间的大部分接触顶点不会突然发生相对滑动。基于这一观察结果，我们首先利用基于 GPU 的可微分接触模块来推断手部顶点到物体之间的带符号距离函数 $sdf({\mathbf{V}}_{hand})$。然后，我们找到 SDF 值小于 0.1 的接触点 ${\mathbf{v}}_t$。$t$ 和 $t-1$ 之间的相对滑动为,

$$L_{sliding}(\theta ,\mathbf{r},\mathbf{t})=||({\mathbf{v}}_t-{\mathbf{r}}_t)({\mathbf{r}}_t^{-1}{)}^{\top }-({\mathbf{v}}_{t-1}-{\mathbf{t}}_{t-1})({\mathbf{r}}_{t-1}^{-1}{)}^{\top }||$$

此外，考虑到 SDF 结果，我们通过惩罚 SDF 负值来降低渗透率。

$$L_{penetration}(\theta ,\mathbf{r},\mathbf{t})=\mathbf{min}(0,-sdf({\mathbf{V}}_{hand}))\text{\hspace{1em}(3)}$$

平滑度损失。 为了增强手和物体在时间上的连续性，我们对连续两帧中物体和手的突然变化进行惩罚。对于物体，我们在当前帧 ${\mathbf{V}}_t$ 和上一帧 ${\mathbf{V}}_{t-1}$ 中的物体顶点之间计算 L2 损失。对于手，我们计算两个帧 ${\theta }_t$、${\theta }_{t-1}$ 中手的姿势之间的 L2 损失、

$$L_{con}=\Vert {\mathbf{V}}_t-{\mathbf{V}}_{t-1}{\Vert }_2^2+\Vert {\theta }_t-{\theta }_{t-1}{\Vert }_2^2.\text{\hspace{1em}(4)}$$

在实验过程中，我们还观察到，物体通常会在几个帧中出现抖动。因此，我们添加了一个平滑项来消除物体速度的振荡、

$$L_{smo}=\Vert ({\mathbf{V}}_t-{\mathbf{V}}_{t-1})-({\mathbf{V}}_{t-1}-{\mathbf{V}}_{t-2}){\Vert }_2^2.\text{\hspace{1em}(5)}$$

D. 基于优化的改进

总之，渲染先验的损失是

$$L_{render}={\lambda }_1{L}_{image}+{\lambda }_2{L}_{mask},\text{\hspace{1em}(6)}$$

而物理学启发的损失为

$$L_{physics}={\lambda }_3{L}_{sliding}+{\lambda }_4{L}_{penetration}+{\lambda }_5{L}_{con}+{\lambda }_6{L}_{smo},$$

其中 $\lambda$ 是损失项的权重。利用这些可微分的损失项，我们使用基于梯度的优化方法（如 Adam [59]）来优化手的姿态 $\theta$ 和物体 $\mathbf{r},\mathbf{t}$。

E. 基于过滤的跟踪

除了基于优化的流程外，我们还可以在更轻量级的管道中使用可微分先验（图 3）。在本研究中，我们以扩展卡尔曼滤波器（EKF）[10]为例。EKF 可以在动态系统中进行状态估计

$${\mathbf{x}}_t=f({\mathbf{x}}_{t-1},{\mathbf{u}}_t)+{ϵ}_s,{\mathbf{z}}_t=h(x_t)+{ϵ}_o,\text{\hspace{1em}(7)}$$

其中，$\mathbf{x}$ 为状态，$\mathbf{u}$ 为控制，$\mathbf{z}$ 为观测值，${ϵ}_s$ 和 ${ϵ}_o$ 为噪声，$f(\cdot )$、$h(\cdot )$ 分别为状态和观测值的可微分函数。利用 EKF，我们可以在给定观测值 ${\mathbf{z}}_t$ 和控制值 ${\mathbf{u}}_t$ 的情况下，计算出隐藏状态 ${\mathbf{x}}_t$ 的估计值 ${\hat{\mathbf{x}}}_t$。

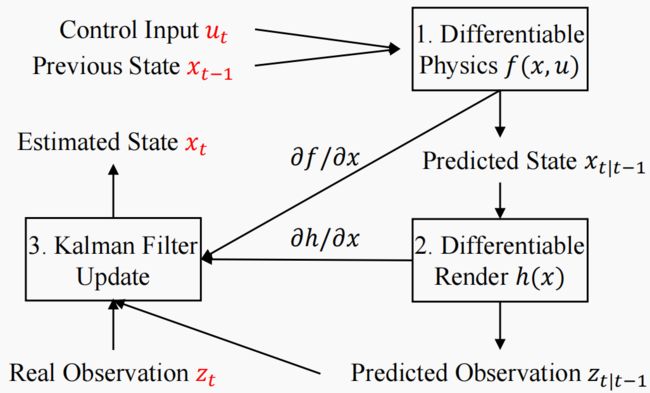
图 3：EKF 滤波过程示意图。 有了（1）可微分物理 $f$ 和（2）计算雅各比的渲染 $h$ 模块，（3）扩展卡尔曼滤波器（EKF）就能根据控制信号、观测数据和先前估计的状态进行状态估计。

手-物体系统的状态为 ${\mathbf{x}}_t=({\theta }_t,{\mathbf{r}}_t,{\mathbf{t}}_t)$。利用这些姿态参数（以及已知的物体模型和形状参数 $\beta$），我们可以重建整个场景。对于现实生活中的大多数情况和现有数据集中的几乎所有情况，手都可以被模拟为执行器，而物体则主要是被动的。因此，系统的控制输入是手的姿势 ${\mathbf{u}}_t=\theta$。

由于可微分渲染器可以输出各种量（二维关键点、边界框、全图像集），我们可以选择的观察对象也很灵活。例如，指尖的二维位置可以作为唯一的反馈监督。那么观察函数为

$$h({\mathbf{x}}_t)=S_{tips}\cdot {\mathbf{V}}_{hand}({\theta }_t),\text{\hspace{1em}(8)}$$

其中，$S_{tips}\in {\mathbb{R}}^{5\times 778}$ 是一个单击编码矩阵，用于从手掌中选择指尖。

更具挑战性的部分是构建动力学函数 $f(\cdot )$。直接的解决方案是使用可变全动力学模型来描述系统。然而，MANO 参数无法提供手部的驱动信号（如肌肉收缩）。因此，我们选择使用更简单、更稳健的准静态动力学。如果手在时间步长 $t-1$ 时与顶点 ${\mathbf{v}}_{t-1}=S_{contact}\cdot {\mathbf{V}}_{hand}({\theta }_{t-1})$上的物体接触，我们假设顶点上从 ${\mathbf{v}}_{t-1}$ 到 ${\mathbf{v}}_t\in {\mathbb{R}}^{n_{contact}\times 3}$ 的相对滑动很小。旋转 $\mathbf{R}$ 和平移 $\mathbf{T}$ 的估计值为

$$\begin{gathered} \mathbf{U}\Sigma {\mathbf{V}}^{†}=svd(\tilde{\mathbf{v}}{t}_{t-1}^{\top }{\tilde{\mathbf{v}}}_t) \\ {\mathbf{R}}_t=({\mathbf{UV}}^{†}{)}^{\top }{\mathbf{R}}_{t-1} \\ {\mathbf{T}}_t={\bar{\mathbf{v}}}_t-{\bar{\mathbf{v}}}_{t-1}({\mathbf{UV}}^{†})+{\mathbf{T}}_{t-1}\text{\hspace{1em}(9)} \end{gathered}$$

其中，$\tilde{\mathbf{v}}=\mathbf{v}-\bar{\mathbf{v}}$ 为接触顶点减去其中心点 $\bar{\mathbf{v}}$，$svd(\cdot )$ 为奇异值分解。

有了可变观测值 $h(\cdot )$（公式 8）和动态值 $f(\cdot )$（公式 9），我们就可以使用 EKF 跟踪和估计状态 ${\mathbf{x}}_t=({\theta }_t,{\mathbf{r}}_t,{\mathbf{t}}_t)$。

4. 实验

在本节中，我们将我们的可微分先验应用于五种场景： (a) 用于机器人操纵的物体姿态估计；(b) 姿态估计；© 基于滤波的跟踪；(d) 接触细化；(e) 人-物姿态估计。我们的方法可以在各种任务中取得相当或更好的结果。

A. 真实世界中的机器人手和物体迭代

我们的方法可广泛应用于各种场景，包括机器人手和物体交互。为了证明这一点，我们设计了一个机器人手操作任务。我们首先使用校准过的英特尔 RealSense 摄像头记录 Allegro 机器人手与 YCB 物体[58] 交互的 RGB 图像序列，并记录相应的手部姿势参数。然后，我们仅使用 RGB 图像[5]来预测物体的初始姿态。根据 Pointrend [56] 预测的手部姿态参数和分割掩码计算出机器人手部配置。然后，我们使用管道来优化物体姿态 $\mathbf{r},\mathbf{t}$。图 4 显示了我们方法的优化结果。结果表明，即使在机器人手部交互场景中，我们的方法也能生成准确的物体姿态。

图 4：真实世界姿势估计。(a) 我们使用校准过的摄像头记录了一只机器人手在真实世界中操纵一个饼干盒的过程。(b) 使用 [5] 进行初始化。我们观察到 © 我们的方法可以恢复盒子的变换。

B. 姿势估计

1. ) 数据集和度量标准： 数据集。 HO3D 数据集[11]是一个真实的手-物交互数据集，包含来自超过 65 个序列的约 80K 张图像。它使用了 YCB 数据集[58]中的 10 个模型。HO3D 数据集的评估是通过在线服务器进行的。我们报告了所有方法在该数据集评估分区上的表现。Dex-YCB 数据集[38]由 1,000 个序列的 582K 张图像组成，10 个受试者从 8 个摄像机视角抓取 20 个不同的 YCB 物体[58]。它是目前最大的真实手-物交互数据集。在这项工作中，我们报告了我们的方法在该数据集 S0 测试部分的性能。根据文献 [40]，我们过滤掉了包含左手或手未与物体接触的帧。衡量标准。 在表 III 中，我们通过将物体顶点投影到图像平面并计算地面实况顶点与预测顶点之间的倒角距离来测量二维误差。三维误差是原始三维空间中的倒角距离。我们还报告了手和物体之间的平均穿透体积，以衡量这些方法处理交互的能力。这一指标称为碰撞。在表 II 中，我们计算了联合误差、网格误差和联合 AUC（ROC 曲线下面积）。对于关节误差和网格误差，我们报告了 Procrustes 对齐前后的结果，其中 Procrustes 对齐改变了估计姿势的全局旋转、平移和缩放，使其与ground truth相匹配。

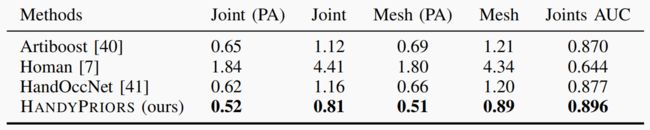
表二：手部姿态估计评估。我们在 DexYCB 数据集[38]上测量了联合误差（厘米）、网格误差（厘米）和联合 AUC。PA 是指 Procrustes Alignment。

表 III： 物体姿态估计的定量评估。在 HO3D [11] 和 DexYCB 数据集 [38] 上，我们的方法与 Semi [5]、Artiboost [40]、Homan [7] 进行了比较。我们报告了二维（厘米）和三维（厘米）误差。

2. ) 基于优化的改进： 我们将第 III-D 节中介绍的基于优化的方法与 Semi[5]、Artiboost[40]、Homan[7] 的姿势估计任务进行了比较。在 HO3D 数据集中，我们测试了评估拆分中的三个对象： 芥末瓶（SM11）、肉罐（MPM10-15）和漂白剂清洁器（SB11, 13）。表 III 显示，在估计物体姿态方面，我们的方法优于其他方法。在碰撞指标方面，我们的方法也取得了不相上下的结果。表 II 显示了与 Artiboost [40]、Homan [7] 和 HandOccNet [41] 相比的手部预测结果。我们的方法也比 [41] 的初始化方法有所改进，在所有指标上都达到了最佳准确度。图 5 显示了一些定性预测结果。与其他方法相比，我们的优化结果与图像更加吻合，手与物体之间的相对位置也更加合理。

图 5：姿势估计结果。 我们将手和物体的姿势估计结果与其他方法进行了比较，并将投影在原始图像上的三维网格可视化。我们的方法对交互场景进行了合理的联合估计。

3. ) 消融研究： 在这一部分，我们研究了不同损失项对估算结果的影响。所有实验都在 HO3D 数据集[11]的评估集 SM1 中进行。表 I 列出了量化结果。从预训练网络[5]的初始化开始，添加渲染损失项${\mathcal{L}}_{rendering}$ 可以大幅提高性能，尤其是在三维误差方面，因为它可以调整深度方向上的平移误差。此外，添加物理损失项 ${\mathcal{L}}_{physics}$ 可以减少预测序列中的穿透和振荡，从而进一步改善结果。

表 I： 消融研究。我们对优化管道（左栏）和过滤管道（右栏）进行了烧蚀研究。对于优化，2D 和 3D 误差（厘米）随着渲染 ${\mathcal{L}}_{render}$ 和物理损耗 ${\mathcal{L}}_{physics}$ 的逐渐增加而减小。过滤比优化管道快得多，但也会降低精度

C. 基于过滤的跟踪

我们采用第 III-E 节所述的跟踪算法来进行姿态估计。我们在 SM1 序列上运行，定性结果如图 6 所示。我们的滤波管道（b）仅以指尖为输入（图中红点），就能获得物体的充分估计结果。与此同时，基于学习的（a）方法[5]在估计物体姿态时会产生巨大误差。

图 6：过滤结果。我们可以看到，过滤管道可以仅用指尖（红点）作为输入来估计物体姿态。即使纯粹基于学习的方法（a、c）失效，它也能提供稳健、连续的估计。

我们还在表 I 中进行了定量实验，将不同的观察结果输入滤波器。${\mathcal{O}}_{hand}$ 使用预测的指尖三维位置作为观测值；${\mathcal{O}}_{object}$ 使用预测的物体中心作为观测值；${\mathcal{O}}_{hand+object}$ 同时使用上述手部和物体信息作为观测值。结果表明，观测点越多，跟踪结果越准确。跟踪方法比优化流水线快得多；但是，由于提供给它的信息较少，精确度也会下降。

D. 触点细化

物理模块可以在预测过程中输出接触信息。给定手和物体的姿势后，我们基于 GPU 的可微分 Warp 内核 [60] 可以为每个手部顶点 $\{{\mathbf{n}}_i,s_i{\}}_{i<n_{hand}}=contact(\theta ,\mathbf{r},\mathbf{t})$输出带符号的距离函数 s 和法线方向 n。根据 ContactOpt [42]，我们为每个顶点定义了一个接触值 $C{O}_i=\mathbf{min}(\frac{1}{s_i},1)$。当一个顶点距离物体在 1 毫米以内$(s_i<1)$时，$C{O}_i=1$ 表示该点处于接触状态。

给定随机初始化的手部姿势后，我们的方法将 ContactPose 数据集 [61] 提供的地面真实接触信息作为目标。由于我们的 $contact(\cdot )$ 模块也是可微分的，因此我们可以通过基于梯度的优化来优化姿势，使其与目标接触状态 $\{C{O}_i,n_i\}$ 匹配。

图 7 显示了优化过程的示例。(a）和（c）是随机输入的手，（b）和（d）是优化后的手与物体的互动。结果与人们在日常生活中处理这些物体的方式相似。

图 7：基于接触的姿势改进的定性结果。给定随机初始姿势（a,c）和所需的接触区域，我们的方法可以使用可变接触模型和基于梯度的优化（b,d）来完善姿势。

E. 推广到人类

我们提出的可微分先验也可应用于人体物体姿态估计。通过 COCO2017 数据集 [57] 中的 RGB 图像，我们使用 [54] 来初始化人和物体的姿势，然后使用 [56] 来预测人和物体的实例分割掩码。随后，我们将管道中的 MANO 手部模型[20]替换为 SMPL 人体模型[62]，后者也是通过姿势 $\theta \in {\mathbb{R}}^{72}$ 和形状 $\beta \in {\mathbb{R}}^{10}$ 参数来描述人体的。按照与手-物优化相同的设置，我们使用可微分渲染和物理先验，通过我们的管道完善人类参数$(\theta ,\beta ,T_{human})$和物体参数$(\mathbf{r},\mathbf{t})$。实验表明，我们的方法可以生成准确的人-物姿势估计。由于无法获得人和物体的真实姿态，我们在表 IV 中报告了人和物体之间的交集（IoU）和穿透体积。图 8 显示了我们方法的定性结果以及管道各组成部分的贡献。(b) 中的渲染损失有助于更好地将 3D 模型与 RGB 图像对齐，但仍存在非物理碰撞。©中的物理损耗对姿势进行了微调，减少了此类穿透。

表四：人体物体姿态估计的定量评估 与 PHOSA [54] 相比，我们的方法可以获得更高的二维 IoU 和更低的碰撞误差$(c{m}^3)$。

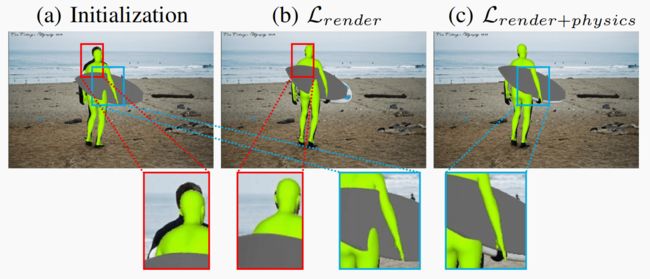
图 8：人体物体姿态细化。(a) 使用 [54] 进行初始化，(b) 仅使用可微分渲染进行细化，© 同时使用可微分渲染和物理模拟器进行细化之间的定性比较。渲染损失有助于对齐图像，而物理损失则可以减少穿透。

5. 结论

在本文中，我们介绍了 HANDYPRIORS，这是一个用于手-物体互动场景中姿势估计的可微分渲染和物理先验框架。针对不同的使用情况，我们提出了两种备选方案：基于优化的姿态细化和基于过滤的跟踪，前者侧重于预测精度，后者侧重于运行速度。我们提出的渲染和物理相关运算器可通过输入的 RGB 图像序列进行自我监督，从而实现闭环优化和跟踪。实验表明，由于采用了统一的通用先验，我们的方法在姿态估计和接触细化任务中取得了相当或更好的结果。我们还证明，我们的方法可应用于机器人手部操纵和人类姿势估计任务。

我们还注意到我们的实施存在一些局限性。首先，如果初始化不佳，优化管道可能会失败。这个问题可以通过在可微分渲染模块中添加边界框或关键点相关术语来缓解。其次，可以通过更快的可微分渲染模块（如 Nvdiffrast [63]）来提高优化性能。第三，目前基于 EKF 的过滤管道有可能输出预测的不确定性。将我们的管道与概率预测相结合将大有可为。