【数据结构】快速排序，归并排序

快速排序

1.hoare版本

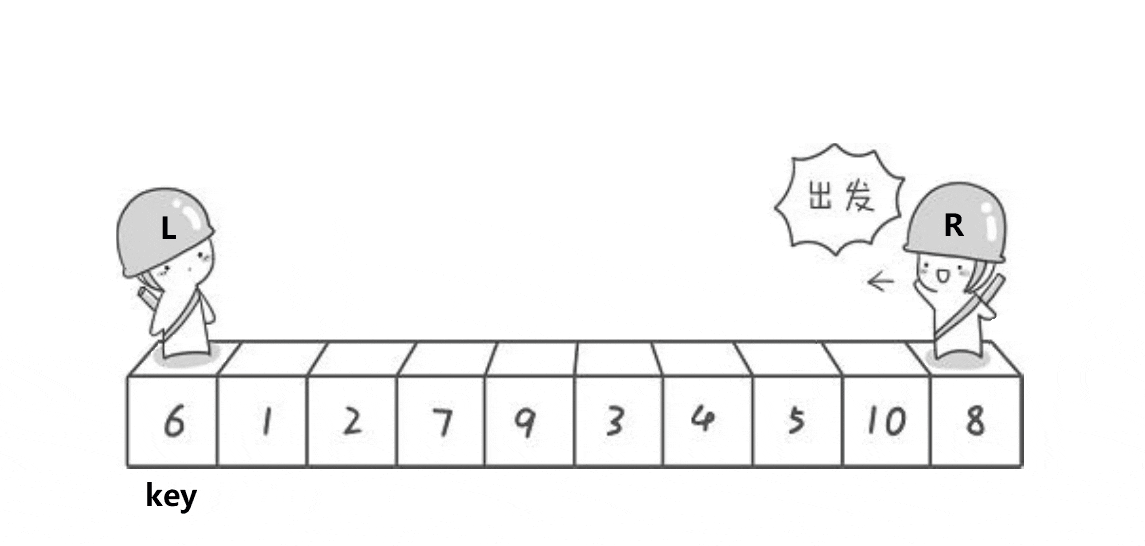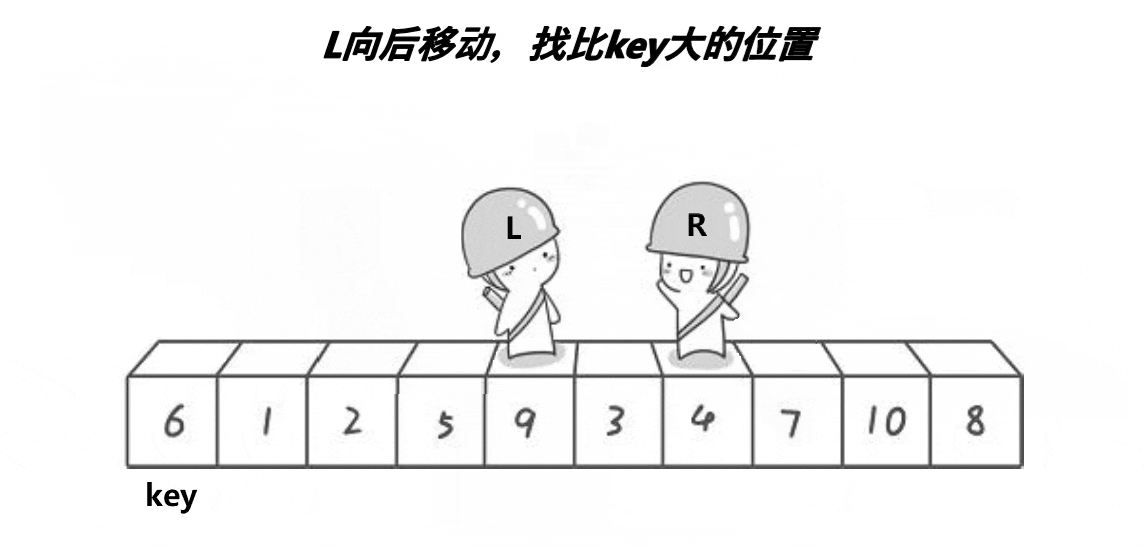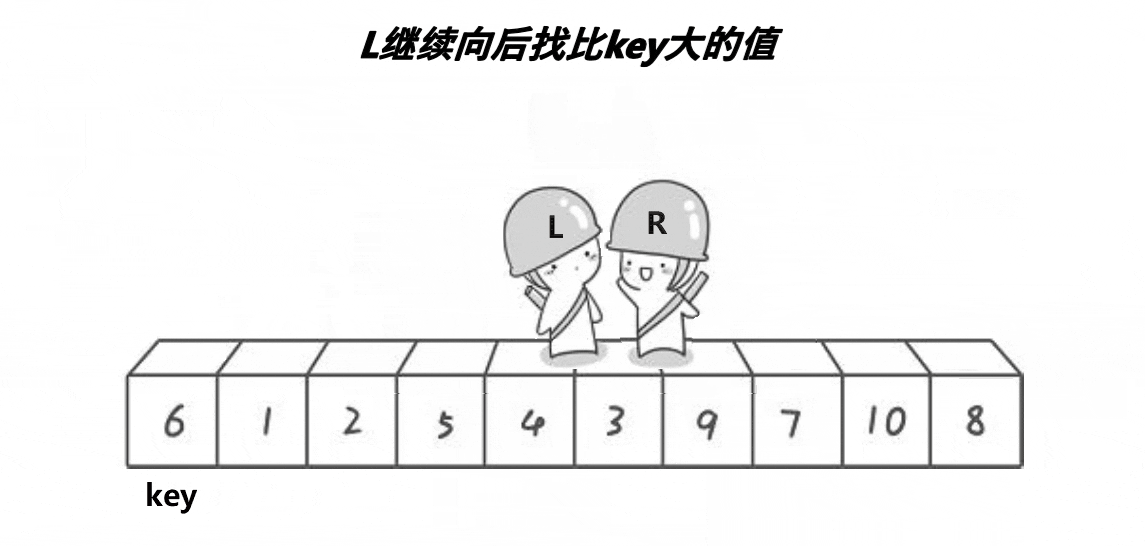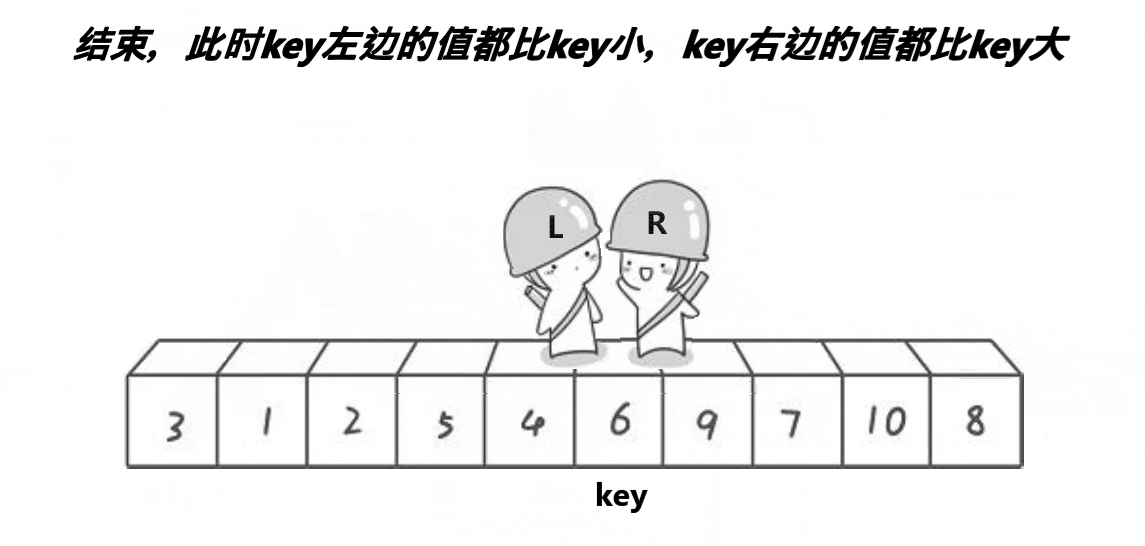
根据动图的演示，整理的思路如下，
1.定义left,right,key。key默认是左边第一个元素，像两个指针，左边找比key大的，右边找比k小的，找到的话，交换二者，往返这个过程，当left与right相遇时，交换key和此时相遇的值.

#include
void swap(int*p,int*q)
{
	int tmp = *p;
	*p = *q;
	*q = tmp;

}
int PartSort1(int* a, int left, int right)
{
	int keyi =left;
	while (left < right)
	{
		while (left<right && a[right]>=a[keyi])
		{
			right--;
		}
		while (left<right && a[left]<= a[keyi])
		{
			left++;
		}
		swap(&a[left],&a[right]);

	}
	swap(&a[keyi], &a[left]);
	return left;

}
int main()
{
	int arr[] = { 6,1,2,7,9,3,4,5,10,8 };
	PartSort1(arr, 0, 9);
	for (int i = 0; i < 10; i++)
	{
		printf("%d ", arr[i]);


	}


}

单趟下来，6出现在正确的位置。
1.为什么大循环是left 当两个小人走到一块去的时候，我们应该交换key位置的值，和相遇时候的值了，而不是让他们两个岔开.
2.为什么在小循环中要加left 假如说数组是10,10,10,10,10,10,10,10,10
在小循环中一直找小，找不到就会越界.
3.return的值有什么用？
return的值相当于分了界，然后就可以分别对子区间使用快排了.

针对每个子区间，使用快排

#include
void swap(int*p,int*q)
{
	int tmp = *p;
	*p = *q;
	*q = tmp;

}
int PartSort1(int* a, int left, int right)
{
	int keyi =left;
	while (left < right)
	{
		while (left<right && a[right]>=a[keyi])
		{
			right--;
		}
		while (left<right && a[left]<= a[keyi])
		{
			left++;
		}
		swap(&a[left],&a[right]);

	}
	swap(&a[keyi], &a[left]);
	return left;

}
void QuickSort(int* a, int begin, int end)
{
	if (begin >= end)
		return;
	int mid=PartSort1(a,begin,end);
	QuickSort(a,begin, mid - 1);
	QuickSort(a,mid+1,end);

}
int main()
{
	int arr[] = { 6,1,2,7,9,3,4,5,10,8 };
	QuickSort(arr, 0, 9);
	for (int i = 0; i < 10; i++)
	{
		printf("%d ", arr[i]);


	}


}

递归结束条件，如果有两个数据的话还能排一次，如果只有一个数据的话就不用排了
1.为什么要右边先走，左边再走，为啥相遇的值一定比key小或者等于key？
情况1：右边找小，找不到小，一直往左走，与key碰面，相遇的值为key;
情况2：右边找到了小，停在那里，左边找大，一直找不到大，相遇点就停在了比key小的那里
情况3：交换值之后，右边一直找不到小，一直走，相遇点就是左边刚交换完，还没有动的比key小的值.
情况4：交换值之后，右边继续移动，找到小停在那，左边找不到大，相遇点就是比key小的.

2.挖坑法

1.创建临时变量key保存最左侧坑位的值，右边找小找到小之后，将找到的小值填到左边的坑位去，这里变成坑位.左边找大，找到大之后，将该值填入右侧的坑位，依次循环，相遇之后，将key放到相遇点

#include
void swap(int*p,int*q)
{
	int tmp = *p;
	*p = *q;
	*q = tmp;

}

int PartSort2(int* a, int left, int right)
{
	int key = a[left];
	int pole = left;
	while (left < right)
	{
		while (left < right && a[right] >=key)
		{
			right--;
		}
		a[pole] = a[right];
		pole = right;

		
		while (left < right && a[left] <= key)
		{
			left++;
		}
		a[pole] = a[left];
		pole = left;
		
	}
	a[left] = key;
	return left;

}
void QuickSort(int* a, int begin, int end)
{
	if (begin >= end)
		return;
	int mid=PartSort2(a,begin,end);
	QuickSort(a,begin, mid - 1);
	QuickSort(a,mid+1,end);

}
int main()
{
	int arr[] = { 6,1,2,7,9,3,4,5,10,8 };
	QuickSort(arr, 0, 9);
	for (int i = 0; i < 10; i++)
	{
		printf("%d ", arr[i]);


	}


}

3.前后指针法

前后指针法

#include
void swap(int*p,int*q)
{
	int tmp = *p;
	*p = *q;
	*q = tmp;

}
int PartSort3(int* a, int left, int right)
{
	int keyi = left;
	int cur = left + 1;
	int prev = left;
	while (cur<=right)
	{
		if (a[cur] < a[keyi])
		{
			prev++;
			swap(&a[cur], &a[prev]);
		}




		cur++;
    }
	swap(&a[keyi], &a[prev]);
	return prev;

}

void QuickSort(int* a, int begin, int end)
{
	if (begin >= end)
		return;
	int mid=PartSort3(a,begin,end);
	QuickSort(a,begin, mid - 1);
	QuickSort(a,mid+1,end);

}
int main()
{
	int arr[] = { 6,1,2,7,9,3,4,5,10,8 };
	QuickSort(arr, 0, 9);
	for (int i = 0; i < 10; i++)
	{
		printf("%d ", arr[i]);


	}


}

4.快速排序非递归版

采用非递归代替递归分割步骤，当区间只有一个值时，将不在入栈.

#include 
#include 
#include 
void swap(int*p,int*q)
{
	int tmp = *p;
	*p = *q;
	*q = tmp;

}
typedef struct Stack//定义一个栈的结构体变量	
{
	int* a;
	int top; // 栈顶
	int capacity; // 容量
}Stack;
void StackInit(Stack* ps)
{
	assert(ps);//断言，防止为空指针
	ps->a = NULL;//所指向的地址为空
	ps->capacity = ps->top = 0;//容量和栈中元素个数均为0
}
void StackPush(Stack* ps, int data)
{
	assert(ps);
	if (ps->capacity == ps->top)//如果栈中的元素个数等于栈的容量时考虑扩容，
	{
		int newcapcity = ps->capacity == 0 ? 4 : ps->capacity * 2;//如果刚开始时都等于0，就先给4个空间大小，后面如果满的话，容量扩大1倍
		int* newnode = (int*)realloc(ps->a, sizeof(int) * newcapcity);//申请空间，将申请好的空间首地址传给newnode指针
		assert(newnode);//断言，防止malloc失败
		ps->a = newnode;//将newnode保存的申请空间的首地址传给ps->a,让ps->a指向创建好的空间
		ps->capacity = newcapcity;//容量大小更新为新容量大小



	}
	ps->a[ps->top] = data;//像存数组一样存数据
	ps->top++;//指向下一个
}
// 检测栈是否为空，如果为空返回非零结果，如果不为空返回0 
int StackEmpty(Stack* ps)
{
	assert(ps);
	return ps->top == 0;//ps->top为栈中元素个数.==0栈中无元素，无元素要返回1， 无元素ps->t0p==0，这个表达式结果是1，返回1;





}
// 出栈
void StackPop(Stack* ps)
{
	assert(ps);
	assert(!StackEmpty(ps));//防止栈内无元素，继续出栈
	ps->top--;
}
// 获取栈顶元素
int StackTop(Stack* ps)
{
	assert(ps);
	assert(!StackEmpty(ps));
	return ps->a[ps->top - 1];//ps->top为栈中元素个数，由于数组下标是从0开始，所以栈顶元素下标为ps->top-1;

}
// 获取栈中有效元素个数
int StackSize(Stack* ps)
{
	assert(ps);
	return ps->top;

}
// 销毁栈
void StackDestroy(Stack* ps)
{
	assert(ps);
	free(ps->a);//free掉动态申请的内存
	ps->a = NULL;//防止野指针
	ps->capacity = ps->top = 0;//容量和栈中元素个数置为0



}
int PartSort1(int* a, int left, int right)
{
	int keyi =left;
	while (left < right)
	{
		while (left<right && a[right]>=a[keyi])
		{
			right--;
		}
		while (left<right && a[left]<= a[keyi])
		{
			left++;
		}
		swap(&a[left],&a[right]);

	}
	swap(&a[keyi], &a[left]);
	return left;

}
void QuickSort(int* a, int begin, int end)
{
	Stack st;
	StackInit(&st);
	StackPush(&st,end);
	StackPush(&st,begin);
	while (!StackEmpty(&st))
	{
		
		int left = StackTop(&st);
			StackPop(&st);
		int right = StackTop(&st);
			StackPop(&st);

		int mid = PartSort1(a, left, right);

		if (mid + 1 < right)
		{
			StackPush(&st,right);
			StackPush(&st,mid+1);

		}
		if (left < mid-1)
		{
			StackPush(&st,mid-1);
			StackPush(&st,left);

		}








	}

StackDestroy(&st);
}

int main()
{
	int arr[] = { 6,1,2,7,9,3,4,5,10,8 };
	QuickSort(arr, 0, 9);
	for (int i = 0; i < 10; i++)
	{
		printf("%d ",arr[i]);


	}


}

归并排序

基本思想：
归并排序（MERGE-SORT）是建立在归并操作上的一种有效的排序算法,该算法是采用分治法（Divide andConquer）的一个非常典型的应用。将已有序的子序列合并，得到完全有序的序列；即先使每个子序列有序，再使子序列段间有序。若将两个有序表合并成一个有序表，称为二路归并。 归并排序核心步骤：

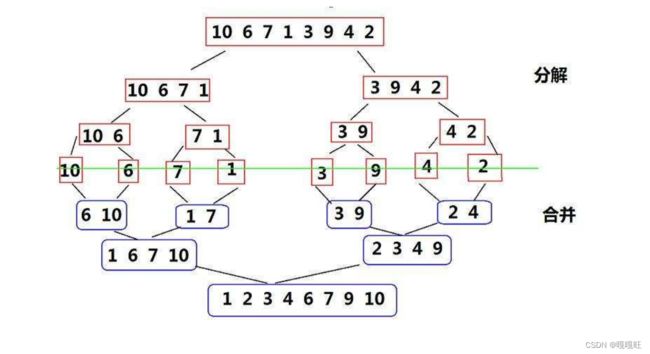
#include 
#include 
#include 
#include
void _MergeSort(int* a, int begin, int end, int* tmp)
{
	if (begin >= end)
		return;
	int mid = (begin + end) / 2;

	_MergeSort(a, begin,mid, tmp);
	_MergeSort(a, mid+1, end, tmp);
	int begin1 = begin;
	int end1 = mid;
	int begin2 = mid + 1;
	int end2 = end;
	int j = begin;
	while (begin1 <= end1 && begin2 <= end2)
	{
		if (a[begin1] < a[begin2])
		{
			tmp[j++] = a[begin1++];
		}
		if (a[begin2] < a[begin1])
		{
			tmp[j++] = a[begin2++];
		}
}
	while (begin1 <= end1)
	{
		tmp[j++] = a[begin1++];

	}
	while (begin2 <= end2)
	{
		tmp[j++] = a[begin2++];

	}
	memcpy(a + begin, tmp + begin, sizeof(int) * (end - begin + 1));





	
}
//归并排序
void MergeSort(int* a, int n)
{
	int* tmp = (int*)malloc(sizeof(int) * n);
	_MergeSort(a, 0, n - 1, tmp);
	free(tmp);
	
}
int main()
{
	int arr[] = { 6,1,2,7,9,3,4,5,10,8 };
	MergeSort(arr, 10);
	for (int i = 0; i < 10; i++)
	{
		printf("%d ",arr[i]);


	}


}

0-0,1-1return回0-1，

2-2return回0-2

归并排序非递归版

void MergeSortNonR(int* a, int n)
{
	int* tmp = (int*)malloc(sizeof(int) * n);
	if (tmp == NULL)
	{
		perror("malloc fail");
	}
	int gap = 1;
	while (gap<n)
	{
		int j = 0;
		for (int i = 0; i < n; i += 2 * gap)
		{
			int begin1 = i;
			int end1 = i + gap - 1;
			int begin2 = i + gap;
			int end2 = i + 2 * gap - 1;
			while (begin1 <= end1 && begin2 <= end2)
			{
				if (a[begin1] < a[begin2])
				{
					tmp[j++] = a[begin1++];
				}
				if (a[begin2] < a[begin1])
				{
					tmp[j++] = a[begin2++];
				}





			}
			while (begin1 <= end1)
			{
				tmp[j++] = a[begin1++];

			}
			while (begin2 <= end2)
			{
				tmp[j++] = a[begin2++];

			}













		}
		memcpy(a, tmp, sizeof(int) * n);
		gap *= 2;

	}
}
int main()
{
	int arr[] = { 6,1,2,7,9,3,4,5 };
	MergeSortNonR(arr, 8);
	for (int i = 0; i < 8; i++)
	{
		printf("%d ",arr[i]);


	}


}

gap=1，两个两个排序，然后整体拷贝回去.
gap=2,四个四个排序，然后整体拷贝回去.
gap=8 八个排序，然后整体拷贝回去.

int main()
{
	int arr[] = { 6,1,2,7,9,3,4,5,10 };
	MergeSortNonR(arr, 9);
	for (int i = 0; i < 9; i++)
	{
		printf("%d ",arr[i]);


	}


}

我们换成9个数据，发现程序崩溃.

void MergeSortNonR(int* a, int n)
{
	int* tmp = (int*)malloc(sizeof(int) * n);
	if (tmp == NULL)
	{
		perror("malloc fail");
	}
	int gap = 1;
	while (gap<n)
	{
		int j = 0;
		for (int i = 0; i < n; i += 2 * gap)
		{
			int begin1 = i;
			int end1 = i + gap - 1;
			int begin2 = i + gap;
			int end2 = i + 2 * gap - 1;
			printf("gap=%d [%d,%d][%d,%d]\n",gap, begin1, end1, begin2, end2);
			while (begin1 <= end1 && begin2 <= end2)
			{
				if (a[begin1] < a[begin2])
				{
					tmp[j++] = a[begin1++];
				}
				if (a[begin2] < a[begin1])
				{
					tmp[j++] = a[begin2++];
				}





			}
			while (begin1 <= end1)
			{
				tmp[j++] = a[begin1++];

			}
			while (begin2 <= end2)
			{
				tmp[j++] = a[begin2++];

			}













		}
		memcpy(a, tmp, sizeof(int) * n);
		gap *= 2;

	}
}

修正边界

void MergeSortNonR(int* a, int n)
{
	int* tmp = (int*)malloc(sizeof(int) * n);
	if (tmp == NULL)
	{
		perror("malloc fail");
	}
	int gap = 1;
	while (gap<n)
	{
		int j = 0;
		for (int i = 0; i < n; i += 2 * gap)
		{
			int begin1 = i;
			int end1 = i + gap - 1;
			int begin2 = i + gap;
			int end2 = i + 2 * gap - 1;
			if (end1 >= n || begin2 >= n)
			{
				break;
			}
			if (end2 >= n)
			{
				end2 = n - 1;
			}
			
			while (begin1 <= end1 && begin2 <= end2)
			{
				if (a[begin1] < a[begin2])
				{
					tmp[j++] = a[begin1++];
				}
				if (a[begin2] < a[begin1])
				{
					tmp[j++] = a[begin2++];
				}





			}
			while (begin1 <= end1)
			{
				tmp[j++] = a[begin1++];

			}
			while (begin2 <= end2)
			{
				tmp[j++] = a[begin2++];

			}

			memcpy(a + i, tmp + i, sizeof(int) * (end2 - i + 1));











		}
		
		gap *= 2;

	}
}
int main()
{
	int arr[] = { 6,1,2,7,9,3,4,5,10 };
	MergeSortNonR(arr, 9);
	for (int i = 0; i < 9; i++)
	{
		printf("%d ",arr[i]);


	}


}

1.修改边界后往回拷贝的就不是n了，而是这个end2 - i + 1
2.如果是9个数据的时候，最后一个数据在gap=8中才开始排序