Matlab 求解非刚性微分方程(ode45)
语法
1、[t,y] = ode45(odefun,tspan,y0)
2、[t,y] = ode45(odefun,tspan,y0,options)
3、[t,y,te,ye,ie] = ode45(odefun,tspan,y0,options)
4、sol = ode45(___)
描述
[t,y] = ode45(odefun,tspan,y0)
其中,tspan = [t0 tf] 为微分方程 odefun 的积分区间,y0 为初始条件
[t,y] = ode45(odefun,tspan,y0,options)
其中,options 可以定义积分设置,例如绝对误差容限
[t,y,te,ye,ie] = ode45(odefun,tspan,y0,options)
sol = ode45(___)
返回一个结构体,可以将该结构体与 deval 结合使用来计算区间 [t0 tf] 中任意点位置的解
示例
1、具有一个解分量的 ODE
y ′ = 2 t , 时间区间为 [ 0 5 ] ,初始条件为 y 0 = 0 y^\prime=2t,\quad 时间区间为 [0\quad 5],初始条件为 y_0=0 y′=2t,时间区间为[05],初始条件为y0=0
tspan = [0 5]; % 积分区间
y0 = 0; % 初始条件
[t,y] = ode45(@(t,y) 2*t, tspan, y0); % 求解计算
plot(t,y,'-o') % 绘图
2、非刚性方程
二阶 ODE
y 1 ′ ′ − μ ( 1 − y 1 2 ) y 1 ′ + y 1 = 0 y_1^{\prime\prime}-\mu(1-y_1^2)y_1^\prime+y_1=0 y1′′−μ(1−y12)y1′+y1=0
改写成一阶 ODE
y 1 ′ = y 2 y 2 ′ = μ ( 1 − y 1 2 ) y 2 − y 1 \begin{aligned} y_1^\prime &= y_2\\ y_2^\prime &= \mu(1-y_1^2)y_2-y_1 \end{aligned} y1′y2′=y2=μ(1−y12)y2−y1
函数文件 vdp1.m 为 μ = 1 \mu=1 μ=1 的微分方程,变量 y 1 y_1 y1 和 y 2 y_2 y2 是二元素向量 dydt 的项 y(1) 和 y(2)。
function dydt = vdp1(t,y)
dydt = [y(2); (1-y(1)^2)*y(2)-y(1)];
使用 ode45 函数、时间区间 [0 20] 和初始值 [2 0] 来解算该 ODE。生成的输出即为时间点 t 的列向量和解数组 y。
[t,y] = ode45(@vdp1,[0 20],[2; 0]);
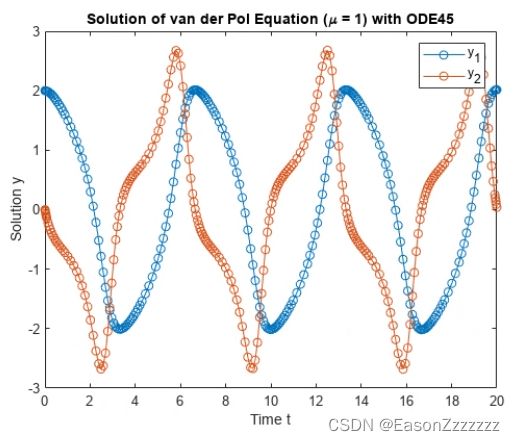
plot(t,y(:,1),'-o',t,y(:,2),'-o')
title('Solution of van der Pol Equation (\mu = 1) with ODE45');
xlabel('Time t');
ylabel('Solution y');
legend('y_1','y_2')