深度学习基础数据结构之张量：从一维到多维

张量在深度学习框架中广泛应用于模型的输入、输出以及中间计算过程。通过支持高维度矩阵运算、记录梯度信息等功能，张量成为实现深度学习算法的关键。

张量是一个多维数据容器，可以用来表示各种数据类型，如数值、图像、音频、文本等。本文将介绍一维、二维、三维和四维张量的形象展示、应用以及对学习理解的作用。

01 一维张量

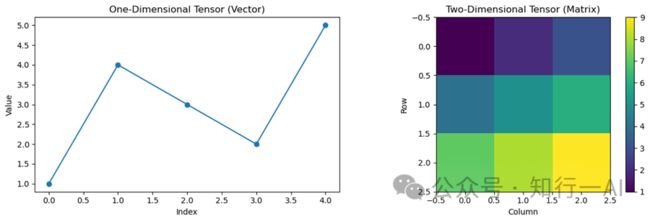
一维张量通常被称为向量，如一维数组[1, 4, 3, 2, 5]，在数学和线性代数中，向量是指具有大小和方向的量，而一维张量（一维数组）正好满足这个定义。一维张量（向量）可以具有弯曲的形状，只要满足向量的定义和线性代数中的性质即可，但向量不一定必须是一条直线。

02 二维张量

二维张量通常被称为矩阵。矩阵是一个包含行和列的二维数据结构，可以表示平面或空间中的数据，每个元素可以通过行和列的索引来定位。在矩阵中，行是水平方向的排列，列是垂直方向的排列，如[[1, 2, 3]]是1行3列。这样，矩阵中的元素可以通过两个索引（行索引和列索引）唯一确定。

二维张量的形象展示可以是一个表格或矩阵，其中每个单元格代表一个数值。二维张量和矩阵之间的关系是很密切的，通常在深度学习和其他数学领域中，这两个术语可以互换使用。

矩阵是一种重要的数学和计算机科学工具，它在各种领域中都有广泛的应用，包括线性代数、图像处理、机器学习等。在深度学习中，二维张量常被用于表示模型的输入和输出数据，如图像、文本和声音等。

import numpy as np

import matplotlib.pyplot as plt

# 创建一个一维张量（向量）

vector = np.array([1, 4, 3, 2, 5])

# 创建一个二维张量（矩阵）

matrix = np.array([[1, 2, 3],

[4, 5, 6],

[7, 8, 9]])

# 可视化一维张量

plt.figure(figsize=(12, 4))

plt.subplot(1, 2, 1)

plt.plot(vector, marker='o')

plt.title('One-Dimensional Tensor (Vector)')

plt.xlabel('Index')

plt.ylabel('Value')

# 可视化二维张量

plt.subplot(1, 2, 2)

plt.imshow(matrix, cmap='viridis', interpolation='nearest')

plt.title('Two-Dimensional Tensor (Matrix)')

plt.xlabel('Column')

plt.ylabel('Row')

plt.colorbar()

plt.tight_layout()

plt.show()

一维张量和二维张量可视化

03 三维张量

三维张量可以将其看作是一个多维数组，其中包含一个或多个二维数组（矩阵）。在数学和计算机科学中，三维张量是一个具有三个维度的数据结构。

第一维度（轴）：通常表示数据集中的样本数量。每个样本可以是一个矩阵。

第二维度（轴）：表示矩阵的行数。

第三维度（轴）：表示矩阵的列数。

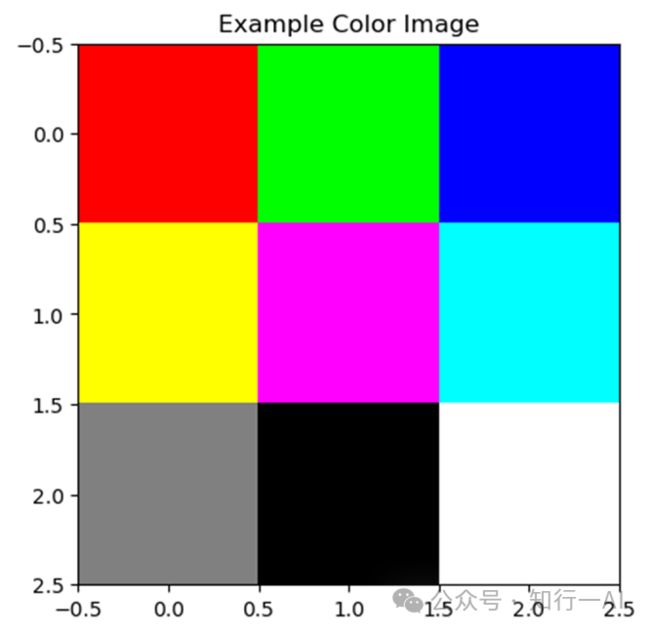
常见的例子是彩色图像，其中每个像素的颜色信息可以表示为一个三维张量，其中第一维度是图像的高度，第二维度是图像的宽度，第三维度是颜色通道（例如，红、绿、蓝）。

import numpy as np

import matplotlib.pyplot as plt

# 创建一个3x3的彩色图像，每个像素包含RGB三个通道的值

color_image = np.array([

[[255, 0, 0], [0, 255, 0], [0, 0, 255]],

[[255, 255, 0], [255, 0, 255], [0, 255, 255]],

[[128, 128, 128], [0, 0, 0], [255, 255, 255]]

], dtype=np.uint8)

# 显示图像

plt.imshow(color_image)

plt.title('Example Color Image')

plt.show()

彩色图像三维数组可视化

在这个例子中，color_image是一个形状为 (3, 3, 3) 的三维张量，其中第一个维度表示图像的高度，第二个维度表示图像的宽度，第三个维度表示颜色通道。图像中的每个像素都由三个值组成，分别代表红色、绿色和蓝色通道的强度。

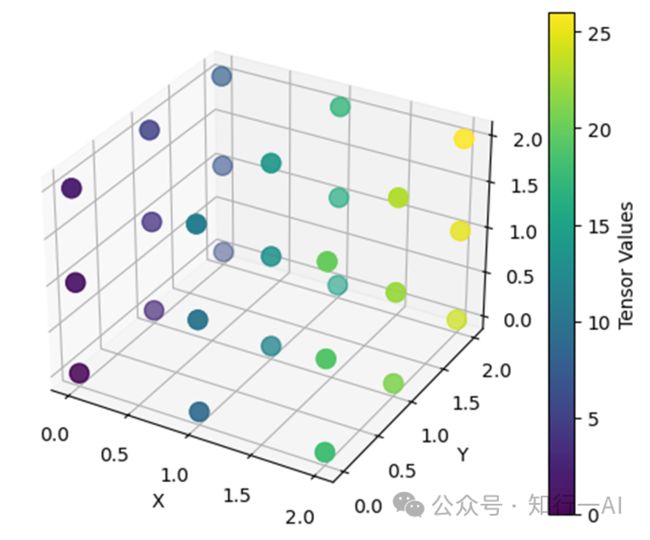
在深度学习中，三维张量常被用于表示具有空间结构的数据，如三维图像、视频和立体声音频等。三维张量的形象展示可以是一个立方体或长方体，其中每个单元格代表一个数值。在实际应用中，彩色图像的三维张量通常包含大量的像素，每个像素都有三个值来表示颜色信息。深度学习中的卷积神经网络（CNN）等模型经常处理这样的张量，以学习图像特征。理解三维张量有助于处理包含多层信息的数据，这在深度学习和其他科学领域中经常遇到。

import numpy as np

import matplotlib.pyplot as plt

from mpl_toolkits.mplot3d import Axes3D

# 创建3x3x3的三维张量

tensor = np.arange(27).reshape((3, 3, 3))

# 获取张量的坐标信息

x, y, z = np.meshgrid(range(tensor.shape[0]), range(tensor.shape[1]), range(tensor.shape[2]), indexing='ij')

# 创建3D图形

fig = plt.figure()

ax = fig.add_subplot(111, projection='3d')

# 绘制三维散点图

ax.scatter(x, y, z, c=tensor.flatten(), s=100, cmap='viridis')

# 设置坐标轴标签

ax.set_xlabel('X')

ax.set_ylabel('Y')

ax.set_zlabel('Z')

# 显示颜色条

cbar = plt.colorbar(ax.scatter(x, y, z, c=tensor.flatten(), s=100, cmap='viridis'))

cbar.set_label('Tensor Values')

# 显示图形

plt.show()

三维张量立体可视化

下面使用使用Mayavi对上文三维张量进行三维可视化

from mayavi import mlab

import numpy as np

# 创建一个3x3x3的三维张量

tensor = np.arange(27).reshape((3, 3, 3))

# 使用Mayavi进行三维可视化

mlab.figure()

mlab.contour3d(tensor)

mlab.show()

使用Mayavi进行三维可视化

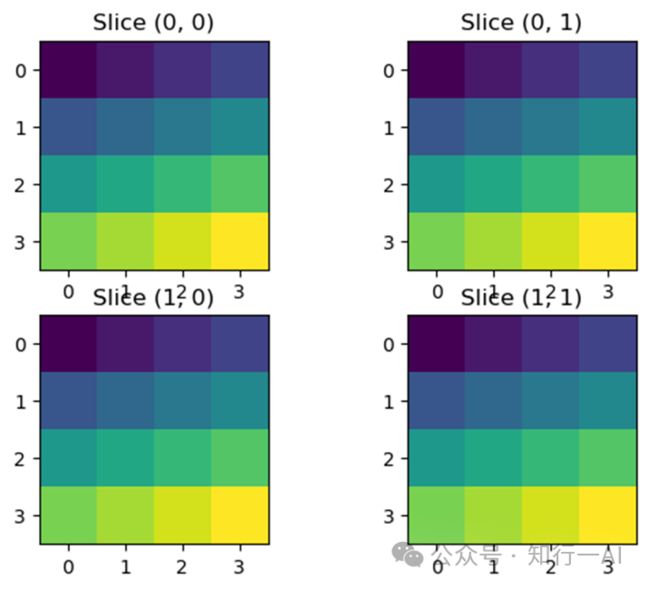
04 多维张量（四维为例）

        

import numpy as np

import matplotlib.pyplot as plt

# Create a 4x4x4x4 tensor using np.arange(256)

tensor = np.arange(256).reshape((4, 4, 4, 4))

# 创建一个2x2的平面，显示四维张量的切片

fig, axs = plt.subplots(2, 2)

# 显示不同切片的颜色

for i in range(2):

    for j in range(2):

        axs[i, j].imshow(tensor[:, :, i, j], cmap='viridis')

        axs[i, j].set_title(f'Slice ({i}, {j})')

plt.show()

05 结尾

本文通过可视化手段，对多维数据——尤其是n维数组（张量）进行了形象化的展示，旨在帮助学习者加深对这一重要概念的理解。

在大学或者其他学习阶段，面对众多复杂且抽象的数学和科学概念，学习时往往会感到困惑和不理解，而影响学习效果。可视化作为一种强大的学习工具，能够将抽象的概念转化为直观、易于理解的图像或模型，从而显著降低认知难度，提升学习效果，可以作为高效的学习辅助力量。

优化后的原文点击查看：

深度学习数据结构：一维到四维张量的可视化

最后关注一下，一起终身成长。