基于黄金正弦算法的函数寻优算法
文章目录
- 一、理论基础
-
- 1、算法原理
- 2、算法伪代码
- 二、仿真实验与分析
- 三、参考文献
一、理论基础
1、算法原理
黄金正弦算法(Golden sine algorithm, Gold-SA)是Tanyildizi等人于2017年提出的新型元启发式算法,该算法的设计灵感来源于数学中的正弦函数,该算法利用数学中的正弦函数进行计算迭代寻优,其优点是收敛速度快、鲁棒性好、易于实现、调节的参数和运算符少。
Gold-SA根据正弦函数与单位圆的关系,可以遍历正弦函数上的所有值即寻遍单位圆上所有的点,同时在其位置更新过程中引入黄金分割数缩小解决方案的空间,以便扫描可能只产生良好结果的区域,很大程度上提高了搜索速度,且使搜索和开发达到良好的平衡。Gold-SA算法的核心过程是其解的更新过程,首先随机产生 s s s个个体的位置,假设优化问题的每个解对应搜索空间中对应个体的位置,并用 X i d ( t ) X_i^d(t) Xid(t)表示 d d d维个体空间中第 t t t次迭代第 i i i个个体的空间位置,可以表示为 X i d ( t ) = ( X i , 1 , X i , 2 , ⋯ , X i , d ) , ( i = 1 , 2 , ⋯ , s ; t = 1 , 2 , ⋯ , t max ) X_i^d(t)=(X_{i,1},X_{i,2},\cdots,X_{i,d}),(i=1,2,\cdots,s;t=1,2,\cdots,t_{\max}) Xid(t)=(Xi,1,Xi,2,⋯,Xi,d),(i=1,2,⋯,s;t=1,2,⋯,tmax), t max t_{\max} tmax为最大迭代次数, P d ( t ) ( t = 1 , 2 , ⋯ , t max ) P^d(t)(t=1,2,\cdots,t_{\max}) Pd(t)(t=1,2,⋯,tmax)为第 t t t次迭代全局最优位置,则第 i i i个个体的位置更新公式如下: X i d ( t + 1 ) = X i d ( t ) ∣ sin ( r 1 ) ∣ + r 2 sin ( r 1 ) ∣ x 1 P d ( t ) − x 2 X i d ( t ) ∣ (1) X_i^d(t+1)=X_i^d(t)|\sin(r_1)|+r_2\sin(r_1)|x_1P^d(t)-x_2X_i^d(t)|\tag{1} Xid(t+1)=Xid(t)∣sin(r1)∣+r2sin(r1)∣x1Pd(t)−x2Xid(t)∣(1)其中, r 1 r_1 r1和 r 2 r_2 r2为随机数, r 1 r_1 r1决定下一次迭代中个体的移动距离, r 1 ∈ [ 0 , 2 π ] r_1\in[0,2\pi] r1∈[0,2π], r 2 r_2 r2决定下一次迭代第 i i i个个体的位置更新方向, r 2 ∈ [ 0 , π ] r_2\in[0,\pi] r2∈[0,π]; x 1 x_1 x1和 x 2 x_2 x2是通过引入黄金分割数得到的系数,这些系数缩小了搜索空间引领个体逐步趋近最优值,保证了算法的收敛性,黄金分割数是一个定义为 5 − 1 2 \frac{\sqrt5-1}{2} 25−1的无理数,记为 τ \tau τ, x 1 = a τ + b ( 1 − τ ) x_1=a\tau+b(1-\tau) x1=aτ+b(1−τ), x 2 = a ( 1 − τ ) + b τ x_2=a(1-\tau)+b\tau x2=a(1−τ)+bτ, a a a和 b b b初始值设置为 − π -\pi −π和 π \pi π,随后 a a a和 b b b随着目标值的变化而变化, x 1 x_1 x1和 x 2 x_2 x2也随之更新,更新方式如下:
- Step 1:
if current value < target value
b = x2, x2 = x1
x1 = a*tau+b*(1-tau)
else
a = x1, x1 = x2
x2 = a*(1-tau)+b*tau
end
- Step 2:
if x1 == x2
a = random1, b = random2
x1 = a*tau+b*(1-tau)
x2 = a*(1-tau)+b*tau
end
2、算法伪代码
二、仿真实验与分析
将该算法与PSO、SCA、WOA进行对比,种群规模 N = 30 N=30 N=30,最大迭代次数 T = 1000 T=1000 T=1000,以30维的F1~F3为例,每个算法独立运算30次,取这30次运算的最优值、最差值、平均值和标准差作为算法性能的度量标准。
结果显示如下:


函数:F1
PSO:best: 57.1829,worst:355.9929,mean:198.6791,std:71.7651
SCA:best: 1.8446e-08,worst:0.17577,mean:0.032715,std:0.056733
WOA:best: 6.6464e-168,worst:2.6232e-151,mean:1.9298e-152,std:5.2718e-152
Gold-SA:best: 0,worst:0,mean:0,std:0
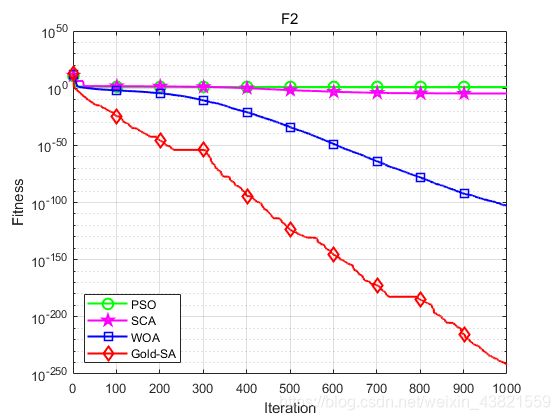
函数:F2
PSO:best: 5.22,worst:22.2049,mean:11.5497,std:3.4386
SCA:best: 2.4384e-08,worst:0.00029691,mean:1.9794e-05,std:5.3646e-05
WOA:best: 6.9506e-115,worst:9.6357e-102,mean:3.8412e-103,std:1.7637e-102
Gold-SA:best: 4.7861e-317,worst:4.2204e-241,mean:1.4068e-242,std:0
函数:F3
PSO:best: 1345.0482,worst:4061.4867,mean:2589.9919,std:787.5485
SCA:best: 134.7844,worst:9533.5216,mean:3443.9262,std:2699.7127
WOA:best: 979.6781,worst:43056.887,mean:22673.5449,std:10381.2685
Gold-SA:best: 0,worst:0,mean:0,std:0
仿真结果表明,Gold-SA算法优于PSO、SCA、WOA算法,有效提高收敛速度和精度。
代码下载链接:https://download.csdn.net/download/weixin_43821559/85461634
三、参考文献
[1] Tanyildizi E, Demir G. Golden Sine Algorithm: A Novel Math-Inspired Algorithm[J]. Advances in Electrical and Computer Engineering, 2017, 17(2): 71-78.
[2] 肖子雅, 刘升. 黄金正弦混合原子优化算法[J]. 微电子学与计算机, 2019, 36(6): 21-25+30.
[3] 于建芳, 刘升, 王俊杰, 等. 融合莱维飞行与黄金正弦的蚁狮优化算法[J]. 计算机应用研究, 2020, 37(8): 2349-2353.
