常用的排序算法
1.冒泡排序
按照冒泡排序的思想,把相邻的元素两两比较,当一个元素大于右侧相邻元素时候,交互他们位置当一个元素小于或者等于右侧相邻元素时候,位置不变。
相应代码实现:
void sort(int array[]){
for(int i =0 ; i< array.length -1 ; i++){
for(int j=0 ;j < array.length -i -1 ; j++){
int temp = 0 ;
if(array[j] > array[j+1]) {
temp = array[j] ;
array[j] = array[j+1];
array[j+1] = temp ;
}
}
}
}这是典型的冒泡写法,使用双循环进行排序。外层循环控制所有的回合,内部循环实现每一轮的冒泡处理,先比较在决定是否交换。
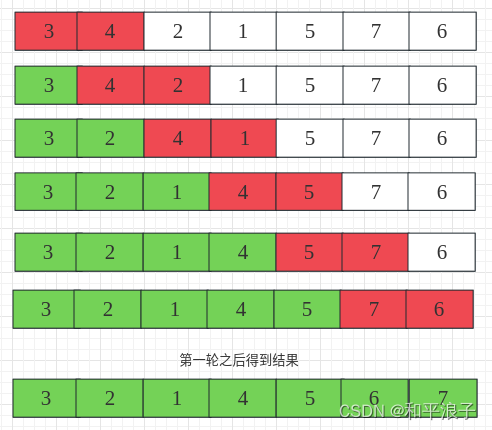
举例说明: int array[] = {3,4,2,1,5,7,6};
那么外层循环第一轮比较图示:
那么可以得到外层循环完毕我们就可以得到一个有序的元素数组啦。 由于每一轮排序都会遍历所有的元素,假设有n轮。 那么2层循环遍历次数是 f(n) = n(n-1)/ 2 ,
所以时间复杂度是O(![]() )。
)。
那么问题就来了,假设的提前排序已经好了,但是排序算法一样会继续下去。 那么这种情况就需要我们优化,下面有集中优化方法。
作标记位
当判断出数列已经是有序啦,那么接下来的无论多少轮都不需要继续下去啦。
优化代码示例如下:
void sort(int array[]){
for(int i =0 ; i< array.length -1 ; i++){
boolean sorted = true ;
for(int j=0 ;j < array.length -i -1 ; j++){
int temp = 0 ;
if(array[j] > array[j+1]) {
temp = array[j] ;
array[j] = array[j+1];
array[j+1] = temp ;
//因为有元素交换,所以不是有序的,标记为false
sorted = false ;
}
}
if(sorted){
System.out.println("提前break i =" + i);
break ;
}
}
}通过代码我们知道sorted是控制外层循环的,那么内循环那层是否也可以优化? 假设一种情况内循环到了一半后后面已经都是有序的啦,但是也会继续下去,这样就导致了比较了多次。 所以这个问题关键就是对有序区域的界定。
有序区界定
代码示例
void sort(int array[]){
int lastIndex = 0 ;
int boder = array.length - 1 ;
for(int i =0 ; i< array.length -1 ; i++){
boolean sorted = true ;
for(int j=0 ;j < boder; j++){
int temp = 0 ;
if(array[j] > array[j+1]) {
temp = array[j] ;
array[j] = array[j+1];
array[j+1] = temp ;
sorted = false ;
lastIndex = j ;
}
}
boder = lastIndex ;
if(sorted){
System.out.println("提前break i =" + i);
break ;
}
}
}我们可以看到border就是无序的数列边界。在每一轮过程中,处于border之后的元素其实就不需要排序啦,肯定是有序的。
鸡尾酒排序
鸡尾酒排序的元素比较和交换是双向的。
假设一组数据 是{2,3,4,5,6,7,1} ,那么第一轮之后我们知道是把7和1交换了得到
{2,3,4,5,6,1,7} 第二轮以此类推6和1交换.. ,最后1和2比较。
第二轮时候可以设想一下,如果1从右到左去比较, 是不是立马就可以排好序啦。 这就是鸡尾酒排序思路,排序过程像钟摆一样。
代码示例
void sort(int array[]){
int temp =0 ;
for(int i =0 ; i< array.length /2 ; i++){
boolean sorted = true ;
// 奇数轮从左到右
for(int j=i ;j < array.length -i -1 ; j++){
if(array[j] > array[j+1]) {
temp = array[j] ;
array[j] = array[j+1];
array[j+1] = temp ;
// 有交换元素,所以不是有序的,标记为false
sorted = false ;
}
}
if(sorted){
System.out.println("提前break i =" + i);
break ;
}
sorted = false ;
// 偶数轮,从右到左
for(int j=array.length-i-1;j>i;j--){
if(array[j] < array[j-1]) {
temp = array[j] ;
array[j] = array[j-1];
array[j-1] = temp ;
// 有交换元素,所以不是有序的,标记为false
sorted = false ;
}
}
if(sorted){
System.out.println("提前break i =" + i);
break ;
}
}
}这段代码就是鸡尾酒排序的实现,代码外层控制所有排序回合,大循环里面包含2个小循环,第一个从左到右比较并且交换。,第二个小循环从右到左开始比较并且交换。
2.快速排序
同冒泡排序一样,快速排序也属于交换排序,通过元素的之间的比较和交换位置来达到排序的目的。 不同的是,快速排序在没一轮都是挑选一个基准元素,并且让比它大的元素移动到一边,比他小的元素移动到另一边,从而把数据拆解成两个部分,这种思路就是分治法。
2.1 分治法
2.1.1 双边循环法
分别在数组头尾设置两个指针left 和 right ,其中left和right的值是数组索引。 并且将头部元素作为基准值pivot,pivot的值是数组索引。
规则:
1. 先判断右指针和基准值,如果右指针指向的元素值大于等于基准位置元素值或者不与左指针重合就向前移动。 否则停止移动。
2. 在判断左指针和基准值,如果左指针指向的元素值小于等于基准位置元素值或者不与右指针重合就像右移动,否者停止移动。
3. 判断是否左右指针重合?
未重合: 交换左指针索引位置的元素值合和右指针的元素值。交互完毕,再回到第1步继续往下执行。 (重复1,2,3动作)
重 合: 将重合指针索引位置的元素值与基准位置的值进行交换。此轮排序结束。
核心代码示例:
private fun sort(arr:IntArray,first:Int ,last:Int){
if(first>=last){
return
}
var temp :Int
var left = first
var right = last
while (true){
// 判断右指针与基准值 ,如果大于或等于基准值元素,且不与左指针重合 ,向前,否者停止移动
while (arr[right] >= arr[first] && left< right) {
right --
}
// 再判断左指针与基准值 ,如果小于或等于基准值元素,且不与右指针重合 ,向后,否者停止移动
while (arr[left] <= arr[first] && left< right){
left ++
}
// 判断是否重合
if(left ")
}
println("")
// [first,last] 第一轮排序已经完成
// 此时左子数组所以在[fist, left-1] 的元素都是小于或者等于当前基准元素的
// 右数组索引[left+1,last] 的元素都是大于或者等于都给你钱基准元素的
sort(arr,first,left-1)
sort(arr,left+1, last)
} 2.1.2单边循环法
双边循环法从数组的两边交替遍历原数组,虽然更加直观,但是代码实现相对繁琐。而单边循环法则简单得多,只从数组的一边对元素进行遍历和交换。
1. 初始化
- 将头部元素作为基准值pivot,其中pivot的值是数组索引。
- 定义mark指针初始时指向头部位置,作用是:保证索引从头部位置的下一个位置到mark位置的元素都是小于基准元素的。
- 定义travel指针初始时指向头部位置的下一个位置,作用是:遍历当前数组 。
2. travel指针向后移动,找到第一个小于基准元素值的元素或指针超出数组最大索引,就停止移动。
2. 判断travel是否超出当前数组最大索引
核心代码示例:
private fun quickSort(arr:IntArray,startIndex: Int,endIndex: Int){
if(startIndex >= endIndex){
return
}
val pivotIndex:Int = partition(arr,startIndex,endIndex)
quickSort(arr,startIndex,pivotIndex-1)
quickSort(arr,pivotIndex +1,endIndex)
}
private fun partition(arr:IntArray,startIndex:Int,endIndex:Int):Int {
val pivot = arr[startIndex]
var mark = startIndex
for(i in startIndex +1 .. endIndex){
if(arr[i] < pivot){
mark ++
val p = arr[mark]
arr[mark] = arr[i]
arr[i] = p
}
}
arr[startIndex] = arr[mark]
arr[mark] = pivot
return mark
}2.1.3 非递归实现
递归就是自己不断调用自己的方法,直到有了突破口,才停止递归。进入一个方法就等于入栈,方法执行完毕就等于出栈,栈中没有了元素,也就停止了运行,所以根据这一点,是可以通过栈来实现快速排序的。绝大多数递归逻辑都可以使用栈的方式来替代。
代码示例:
// 非递归
private fun qSort(arr: IntArray,startIndex: Int,endIndex: Int){
val quickSortStack = Stack>()
// 将整个数列的起动下标,以哈希的形式入栈
val rootParam = HashMap()
rootParam["startIndex"] = startIndex
rootParam["endIndex"] = endIndex
quickSortStack.push(rootParam)
while (!quickSortStack.isEmpty()){
// 栈顶元素出栈,得到起止下标
val param = quickSortStack.pop()
// 得到基准元素
val startIndexV = param["startIndex"] ?:0
val endIndexV = param["endIndex"] ?:0
val pivotIndex= sort(arr, startIndexV, endIndexV)
if(startIndexV < pivotIndex -1) {
val leftParam = HashMap()
leftParam["startIndex"] = startIndexV
leftParam["endIndex"] = pivotIndex -1
quickSortStack.push(leftParam)
}
if(pivotIndex +1 < endIndexV){
val rightParam = HashMap()
rightParam["startIndex"] = pivotIndex +1
rightParam["endIndex"] = endIndexV
quickSortStack.push(rightParam)
}
}
}
private fun sort(arr: IntArray,startIndex: Int,endIndex: Int):Int {
val pivot = arr[startIndex]
var mark = startIndex
for(i in startIndex+1 .. endIndex) {
if(arr[i] < pivot){
mark ++
val p = arr[mark]
arr[mark] = arr[i]
arr[i] = p
}
}
arr[startIndex] = arr[mark]
arr[mark] = pivot
return mark
} 通过上述分析,快速排序的平均时间复杂度尾(Onlogn),极端情况下的时间啊in复杂度是O(![]() ) 。
) 。
3.堆排序
最大堆的堆顶是整个堆中的最大元素 。最小堆的堆顶是整个堆中的最小元素 。二叉树的构建、删除、自我调整的基本操作就是实现堆排序的基础。
堆排序的步骤:
1. 把无序的数组构建成二叉树。需要从小到大排序,则构建成最大堆;需要从大到小排序,则构建成最小堆。
2. 循环删除堆顶元素,替换二叉堆的末尾,调整堆的产生新的堆顶。
代码实现如下:
/**
* 下沉调整
* @param p 父节点
* @param len 堆的有效大小
*/
private fun downAdjust(arr: IntArray, p:Int ,len:Int ) {
var parentIndex = p
var temp = arr[parentIndex]
var childIndex = 2* parentIndex +1
while (childIndex< len){
// 如果有右孩子,且右孩子大于左孩子的值 ,则定位到右孩子
if(childIndex +1 < len &&arr[childIndex+1] > arr[childIndex]){
childIndex ++
}
// 如果父节点大于任何一个孩子的值,则直接跳出
if(temp >= arr[childIndex]){
break
}
// 无需真正交换,单向赋值即可
arr[parentIndex] = arr[childIndex]
parentIndex = childIndex
childIndex = 2 * childIndex + 1
}
arr[parentIndex] = temp
}
private fun heapSort(arr: IntArray){
// 1. 把无序构建成最大堆
for(i in (arr.size -2) /2 downTo 0 ) {
downAdjust(arr,i,arr.size)
}
// 2. 删除堆顶元素,移到集合尾部,调整推产生新的对顶
for(i in arr.size -1 downTo 1 ){
var temp = arr[i]
arr[i] = arr[0]
arr[0] = temp
// 下沉调整最大堆
downAdjust(arr,0,i )
}
}4.计数排序和桶排序
4.1计数排序
利用元素下标来帮助排序 。
代码示例:
private fun countSort(arr: IntArray):IntArray{
// 1. 得到数列的最大值
var max = arr[0]
for (i in arr.indices){
if(arr[i] > max){
max = arr[i]
}
}
// 2. 根据数列最大值确定统计数组的长度
val countArray = IntArray(max +1)
for(i in countArray.indices){
countArray[arr[i]] ++
}
// 3. 输出遍历结果
var index = 0
var sortedArray = IntArray(arr.size)
for(i in countArray.indices){
for (j in 0 until countArray[i]){
sortedArray[index ++] = i
}
}
return sortedArray
}优化版本:
private fun countSort2(arr: IntArray):IntArray{
// 1. 得到数列的最大值,最小值
var max = arr[0]
var min = arr[0]
for (i in 1 until arr.size){
if(arr[i] > max){
max = arr[i]
}
if(arr[i] < min){
min = arr[i]
}
}
val d = max -min
// 2. 根据数列最大值确定统计数组的长度
val countArray = IntArray(d +1)
for(i in countArray.indices){
countArray[arr[i] - min ] ++
}
// 3. 统计数组做变形,后面的元素等于前面的元素之和
for (i in 1 until countArray.size){
countArray[i] += countArray[i -1 ]
}
// 3. 倒序遍历原始数列,从统计数组找到正确位置,输出到结果数组
val sortedArray = IntArray(arr.size)
for (i in arr.size-1 downTo 0 ){
sortedArray[countArray[arr[i] - min]] = arr[i]
countArray [arr[i] - min] --
}
return sortedArray
}局限性:
1. 当数列最大和最小值差距过大时,并不适合用计数排序
2. 当数列元素不是整数时,也不适合用计数排序。
4.2桶排序
是一种线性时间的排序算法。
1. 创建桶,并确定没一个桶的区间范围
2. 遍历原始数列,把元素对号入座放入各个桶中。
3. 每个桶内的元素分别进行排序
4. 便利所有的桶,输出所有元素。
代码示例:
private fun bucketSort(arr:DoubleArray):DoubleArray{
// 1. 得到最大值,最小值 ,并且计算差值 d
var max = arr [0]
var min = arr[0]
for (i in 1 until arr.size) {
if(arr[i] >max) {
max= arr[i]
}
if(arr[i] < min){
min = arr[i]
}
}
var d = max - min
// 2. 初始化桶
val bucketNum = arr.size
val bucketList = ArrayList>(bucketNum)
for(i in arr.indices){
bucketList.add(LinkedList())
}
// 3.
for(i in arr.indices){
val num = ( (arr[i] - min) * (bucketNum -1) /2 ).toInt()
bucketList[num].add(arr[i])
}
// 4.
for(i in 0 until bucketList.size) {
bucketList[i].sort()
}
//5. 输出全部元素
val sortedArray = DoubleArray(arr.size)
var index = 0
bucketList.forEach {list->
list.forEach {element->
sortedArray[index] = element
index ++
}
}
return sortedArray
} 5.排序算法小结
| 排序算法 | 平均时间复杂度 | 最坏时间复杂度 | 空间复杂度 | 是稳定排序 |
| 冒泡排序 | O( |
O( |
O(1) | 稳定 |
| 鸡尾酒排序 | O( |
O( |
O(1) | 稳定 |
| 快速排序 | O(nlogn) | O( |
O(logn) | 不稳定 |
| 堆排序 | O(nlogn) | O(nlogn) | O(1) | 不稳定 |
| 计数排序 | O(n+m) | O(n+m) | O(m) | 稳定 |
| 桶排序 | O(n) | O(nlogn) | O(n) | 稳定 |