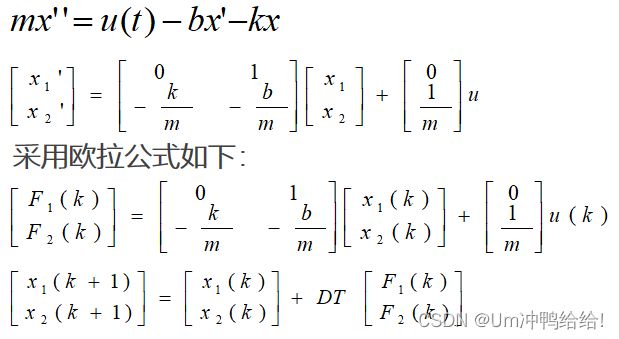系统建模与仿真基础-欧拉法、龙格库塔法Matlab
系统建模与仿真基础-欧拉法、龙格库塔法 附Matlab代码
（本人也在不断学习中，若有错误，欢迎大家批评指正！）
1.系统试验研究方法
1.1解析法
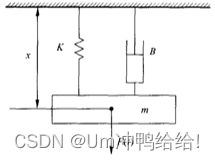
纯理论，比如将实际模型等效成如图所示模型，进而得到描述该系统动态过程的二级常微分方程。
1.2实验法
在实际系统上利用仪器仪表与装置，给系统施加一个信号，通过测量系统响应来确定系统性能。
1.3仿真实验法
在模型上进行系统性能分析与研究，模型分为物理模型和数学模型。我们重点讨论数学模型的数字仿真问题。
2.建模三要素
- 目的要明确
- 方法要恰当
- 结果要验证
2.1 建模方法
a.机理建模(白盒法)：对内部结构或特性清楚的系统，依据基本的物理定律建立数学模型。
b.实验建模(黑盒法)：对内部结构或特性不清楚的系统，根据人工经验或试验得到数据，再经分析、归纳等推理建立系统模型
c.综合建模：在实际工作中通常采用多种方法混合应用。
b.实验建模(黑盒法)：
1.频率特性法（自动控制系统中所学到的知识，后面有时间的话，或许会专门写一篇文章讲解一下）
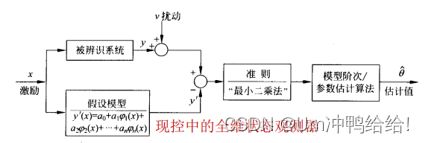
2.系统辨识法：三要素–数据、假设模型、准则（现代控制系统中所学到的知识，后面有时间的话，或许会专门写一篇文章讲解一下）
仿真中最常用的数值积分法
- 欧拉法
- 隐式欧拉法
- 龙格-库塔法
写代码时，根据上述公式来写即可。（其他博客可能与之有些出入，但本质相同）
显示（向前）欧拉法
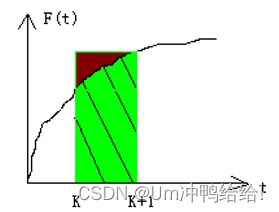
几何解释：欧拉公式用矩形面积近似代替积分面积。步距DT越小，精度越高。
隐式（向后）欧拉法
几何解释：与显示欧拉公式同理，还是用矩形面积近似代替积分面积只不过近似代替的方式有变化，如下图所示。
龙格-库塔法
（这里借用网上图片，具体来源记不清了，若有侵权，联系我，我会删除）
龙格-库塔法要求所求的解具有较好的光滑性。
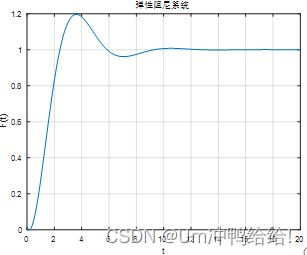
代码（例题）
例1：对于前述弹性阻尼系统模型：
MATLAB程序如下：
clear;
X1= 0; X2= 0;
M= 1; K= 1; B=1;u =1.0; ST=20; DT=0.1;
NP = ST / DT;
for i=1:NP
F1=X2; F2=-K/M*X1-B/M*X2+u/M;
Y(i)=X1;
X1 = X1 + DT * F1; X2 = X2 + DT * F2;
end
plot((1:NP)*DT,Y);
xlabel('t');ylabel('F(t)');grid;
title('弹性阻尼系统');
采用欧拉公式求解：
clear; %清空内存变量
A=[0 1;-1 -1]; B=[0;1];C=[1 0]；%A B C X Y初值
X =[0;0]; u=1; % X 初值，u的大小
ST=20; DT=0.01; NP=ST/DT； %仿真时间步距点数
for i=1:NP;
F=A*X+B*u; X=X+DT*F; Y(i)=C*X;
end
plot((1:NP)*DT,Y);
xlabel('t');ylabel('F(t)');grid;
title('弹性阻尼系统');
两种方法运行结果如下图所示：
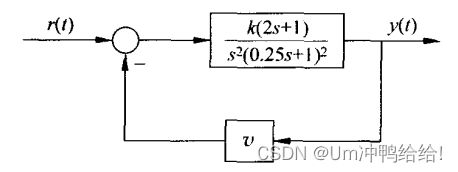
例2.求下图所示系统的阶跃响应y(t)的数值解。
典型闭环系统的仿真程序框图
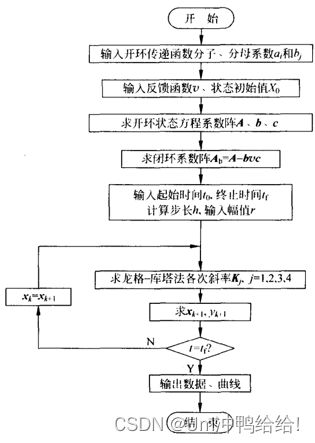
龙格库塔法：面向典型闭环系统数字仿真的程序，从第二部分到程序末尾可编辑为sp3_1.m文件存储起来。使用时，只要进入到MATLAB语言环境，按第一部分格式输入系统参数和运行参数，在调用该文件，即可得到运算结果。
程序框图对应的代码：
%%%1.输入数据
% a=[a0,a1,...,an]
% b=[b0,b1,...,bm]
% v=V0;
% n=n0;
% T0=t0;
% Tf=tf;
% h=h0;
% R=r;
%%%2.形成开、闭环系数阵
b=b/a(1);a = a/a(1); A = a(2:n+1);
A=[rot90(rot90(eye(n-1,n)));-fliplr(A)];
B=[zeros(1,n-1),1]';
m1=length(b);
C=[fliplr(b),zeros(1,n-m1)];
Ab=A-B*C*v;
X=X0';y=0;t=T0;
%3.运算求解
N=round(Tf-T0)/h;
for i = 1:N
K1=Ab*X+B*R
K2=Ab*(X+h*K1/2)+B*R;
K3=Ab*(X+h*K2/2)+B*R;
K4=Ab*(X+h*K3)+B*R;
X=X+h*(K1+2*K2+2*K3+K4)/6;
y=[y,C*X];
t=[t,t(i)+h];
end
%4.输出结果
[t',y']
plot(t,y)
调用sp3_1.m文件，求取y(t)的数值解。
k=1;
a=conv([1 0 0],conv([0.25 1],[0.25 1]));
b=[2*k k];
X0=[0 0 0 0]
v=1;n=4;T0=0;Tf=10;h=0.25;R=1;
sp3_1
[t',y']
最终结果如图所示：
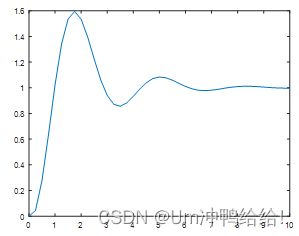
纵轴为y(t)，横轴为时间t。
也可以对开环放大系数k重新赋值，其余参数不变，分析k对反馈系数v的影响作用，再次调用sp3_1.m文件，运行即可。