蓝桥备赛学习总结(一)
真题考察的重点是:暴力枚举(学会计算复杂度与优化)、递归(回溯、剪枝,关键是理解递归套路与原理)、排序(冒泡、插入、希尔、快排)、搜索(深搜、广搜、二分查找)、动态规划、过程模拟、思维、贪心等。以下是早期蓝桥备赛学习的一点个人总结,以后会继续更新完善。
1. 枚举
步骤:
1确定枚举的变量
2确定每个枚举变量对应范围
3确定条件判断语句
枚举常见优化套路:
1减少枚举变量
2缩小枚举范围
3二分查找(复杂度由O(n)—>O(lgn))
4空间换时间(双指针、Hash)
/*
题目:平方十位数
由0~9这10个数字不重复、不遗漏,可以组成很多10位数字。
这其中也有很多恰好是平方数(是某个数的平方)。
比如:1026753849,就是其中最小的一个平方数。
请你找出其中最大的一个平方数是多少?
思路:
1.确定枚举的变量:X
2.确定枚举的范围:[9876543210,1026753849]
3.判断答案符合的条件:判断恰好0-9十个数字、判断是不是完全平方数
但直接枚举枚举平方数显然规模太大,看看如何优化,一种明显的方案是枚举较小的平方根数
1.枚举X的开平方跟Y
2.范围[100000,32043]
3.判断答案符合的条件:平方后的数组成恰好是0-9是个数字
代码实现:
*/
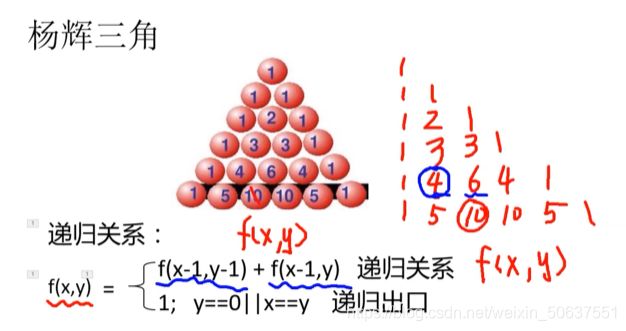
#include 2. 递归
练习策略:
-
循环改递归
-
经典递归问题
写递归的三个步骤:
- 找重复:找到原问题的重复,即找到比原问题规模更小的子问题,可以分解为一个或多个子问题
- 找变化:变化的量作为参数
- 找边界:为了防止递归无限继续下去,给递归找一个合适的出口(判断语句+return)
/*
* f1(n):求n的阶乘-->f(n-1):求n-1的阶乘
* 找重复:n*(n-1)的阶乘,求n-1的阶乘是原问题的重复 (规模更小)——子问题
* 找变化:变化的量作为参数
* 找边界:出口(当n=1时停止)返回一个值,当n=1时函数求1的阶乘,故返回1;
* */
int f1(int n){
if(n==1) return 1;
return n*f1(n-1);
}
/*
* f2(i,j)打印从i到j
* 找重复:先打印i,再打印i+1到j,即打印i+1到j是原问题的重复——子问题
* 找变化:i变成i+1
* 找边界:当i>j时停止
* */
void f2(int i,int j){
if(i>j){
return;
}
cout<<i<<' ';
f2(i+1,j);
}
/*
* f3(int[] arr)数组求和
* 找重复:先求第一个元素,再求剩下的,即求剩下的是原问题的重复——子问题
* 找变化:开始的元素在往后推,所以要加变量f3(int[] arr,int begin)
* 找边界:当i>j时停止
* */
int f3(int[] arr,int begin){
if(begin==arr.length-1){
return arr[begin];
}
return arr[begin]+f3(arr,begin+1);
}
/*
* binarySearch1()在全范围内二分查找
* 可分解为:
* 左边找(递归)
* 中间比
* 右边找(递归)
* */
int binarySearch1(int[] arr,int low,int high,int key){
if(low>high){
return -1;
}
int mid=low+((high-low)>>1);//(low+high)>>>1
// ;右移1位相当于乘以二分之一,防止溢出,位运算也更加高效
int midVal=arr[mid];
if(midVal<key){
return binarySearch1(arr,mid+1,high,key);
}else if(midVal>key){
return binarySearch1(arr,low,mid-1,key);
}else{
return mid;//找到key
}
}
//递归的思想感觉就像是分治的思想,分而治之,把一个复杂的问题分解成很多规模较小的子问题,然后解决这些子问题,把解决的子问题合并起来,大问题就解决了
//经典递归:汉诺塔游戏
//把n个盘从A移动到C
//C是目标盘,B是辅助盘
//等价于
//step1:把前n-1个从A移动到B,C做辅助
//step2:把最底下的一个从A移动到C
//step3:把前n-1个从B移动到C,A做辅助
int sum=0;//移动次数
void printHanoiTower(int n, char from, char to, char help){
if(n==1){
cout<<"move"<<n<<":"<<from<<"->"<<to<<endl;
sum++;
return;
}
printHanoiTower(n-1,from,help,to);
cout<<"move"<<n<<":"<<from<<"->"<<to<<endl;
sum++;
printHanoiTower(n-1,help,to,from);
}
int main() {
printHanoiTower(3,'A','B','C');
cout<<sum;
}
#include3. 排序
基础排序算法:
冒泡(交换)、选择(求最大最小)、插入(挪动数组)、希尔(缩小增量排序)
常用且实用排序:
- 使用STL算法!
- 快速排序!
- 归并排序!
以上三个排序的复杂度都是O(nlogn)
一、sort()函数
头文件:<algorithm>
1.调用方法:sort(第一项的地址,最后一项的地址+1);
如sort(&a[0],&a[n]);或sort(a,a+n);
注意STL的区间是左闭右开;
2.自定义规则的排序:
有时排序的条件不止一个,或不方便对原数据进行排序,就需要自定义比较规则。
这时需要一个写一个函数,把比较的条件解释清楚。
如:
bool cmp(const int &i,const int &j){return w[i]<w[j];}//自定义比较规则
sort(a,a+n,cmp);
二、快速排序
快排是基于比较排序中最快的一种算法。
void quicksort(int *a,int start,int end){
int low=start,high=end;
int temp,check=a[start];
//划分:把比check小的数据放在它的左边,把比check大的数据放在右边
do{
while(a[high]>=check&&low<high) //注意不要写成“low<=high”!
high--;
if(a[high]<check)
temp=a[high],a[high]=a[low],a[low]=temp;
while(a[low]>=check&&low<high) //注意不要写成“low<=high”!
low++;
if(a[low]>check)
temp=a[high],a[high]=a[low],a[low]=temp;
}
while(low!=high);
a[low]=check;
low--;
high++;
//递归:对已经划分好的两部分分别进行快速排序
if(low>start) quicksort(a,start,low);
if(high<end) quicksort(a,high,end);
}
三、归并排序
其他排序算法的空间复杂度是O(1),而并归排序的空间复杂度很大,为O(n)。
int temp[N];
void mergesort(int *a,int start,int end){
if(start+1>=end) return;
//划分阶段、递归
int mid=start+(end-start)/2;
mergesort(a,start,mid);
mergesort(a,mid,end);
//将mid两侧的两个有序表合并为一个有序表
int p=start,q=mid,r=start;
while(p<mid||q<end){
if(q>=end||(p<mid&&a[p]<=a[q]))
temp[r++]=a[p++];
else
temp[r++]=a[q++];
}
for(p=start;p<end;p++){
a[p]=temp[p];
}
}
//并归排序的空间复杂度较大,当数据规模不大时,也可以用插入排序代替并归排序
4. 搜索
- 深搜DFS(一条路走到黑)
操作流程图:
文字描述:
-
清空队列
-
为队列增加起点所在节点
-
在队列首部取出一个节点
-
扫描这个节点所能到达的节点,并将它们放在队列尾部(任意顺序)
-
结束本节点的动作,并准备再次拿取队列首部节点,直到队列为空。
-
回溯和剪枝:
递归调用后就会开启一个分支,如果想这个分支返回后数据恢复到分支开启之前的状态一遍重新开始,就要用到回溯技巧。全排列的交换法、数独游戏、部分和都用到了回溯;
深搜时如果已经明确当前一条路是错误的,无法得到最优解时,就应该中断往下的继续搜索,这种方法称为剪枝。数独游戏和部分和用到了剪枝。
/*
题目:迷宫
下图给出了一个迷宫的平面图,其中标记为1 的为障碍,标记为0 的为可
以通行的地方。
010000
000100
001001
110000
迷宫的入口为左上角,出口为右下角,在迷宫中,只能从一个位置走到这
个它的上、下、左、右四个方向之一。
对于上面的迷宫,从入口开始,可以按DRRURRDDDR 的顺序通过迷宫,
一共10 步。其中D、U、L、R 分别表示向下、向上、向左、向右走。
对于下面这个更复杂的迷宫(30 行50 列),请找出一种通过迷宫的方式,
其使用的步数最少,在步数最少的前提下,请找出字典序最小的一个作为答案。
请注意在字典序中D
/*
*/
//DFS
#include - n皇后问题
DFS求解8皇后问题
#include树的重心
/*思路:
把每个点都模拟删一遍
用dfs求这个节点下面节点的个数,同时这个节点以上节点的个数就可以知道了
*/
#include5. STL库
记住几个常用的函数与其对应头文件
- 容器
vector、set和map这三个容器
set<int> ans;
ans.earse();//删除指定元素
ans.clear();//清空容器
ans.find(val) != ans.end();//说明找到了val这个元素
for(set<int>::iterator it = ans.begin(); it != ans.end(); it++){//从小到大输出容器内元元素
cout << *it << ' ';
}
- 算法
查找:
find()、find_if()、search()
这些函数的底层实现都采用的是顺序查找(逐个遍历)的方式
当区域数据处于有序状态时,就要想到用二分查找提高效率
lower_bound()、upper_bound()、equal_range() 以及 binary_search() ,都是二分查找函数
排序:
前面说过的sort(a,a+n),复杂度是O(nlogn)
全排列next_permutation(a,a+n ),可产生指定范围内的下一个全排列
#include - 函数总结
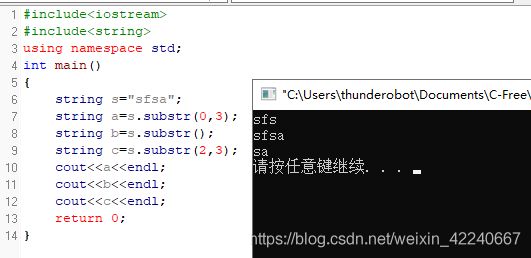
s.substr(pos, len):复制对应区域子字符串
s.substr(pos):复制这个位置之后的字符串
//字符串转成整型数字
//string头文件
string s;
int n;
n=atoi(s.c_str());
6. 细节问题
- 问题:输入若干组数据。。。
因为不知道有多少组以前经常不知道该如何结束程序
看大佬们的题解发现常用的有以下三种方法
1 while(scanf("%d",&n)!=EOF),最常用
2 while(scanf("%d",&n)),取反位
3 while(scanf("%d",&n),n) ,当题目要求输入0停止时使用
//4.30今日错误
人见人爱A-B,题目要求当输入的m和n都为0时,结束程序
一开始写成了这样:while(scanf("%d%d", &m, &n) , m, n)
虽然用例能过,也能正常推出程序,但是应该值判断了m是否为零而没判断n,导致WA
后来想通了之后,如下正确写法!!!
while(scanf("%d%d", &m, &n) , m||n)
-
递归时若需要反复进行相同计算,可以用动态规划,用数组存起来
-
实验思维与猜想:当问题过于复杂,无法联系自己所学知识时,要尽己所能,先解决规模更小的问题,找找问题是否存在规律。
-
大数据放不下可以用数组(如求一百的阶乘,放不下怎么办,这么大的数当然是用数组啦)