数据结构-堆(插入，删除，向下向上调整)

数据结构-堆

1.堆的简介

堆是一类特殊的数据结构的统称，逻辑上是一个完全二叉树，物理上可以使用数组来进行存储。堆满足以下性质

• 堆的跟节点的值总是大于或小于他的分支节点的值
• 堆总是一颗完全二叉树
• 递增或递减的数组一定满足堆的特性，堆的数组不一定完全满足递增或递减。

跟节点是最大值的叫做大根堆，跟节点最小的叫做小根堆。

堆的定义如下:
n个元素的序列{k0,k1,k2…kn-1}当且仅当满足下列条件时,称之为堆
ki<=k2i+1&&ki<=k2i+2(小根堆) ki>=k2i+1&&ki>=k2i+2(大根堆) 这种序列可以对应到一维数组中。将数组看成一个完全二叉树。并且所有分支节点的值都大于等于或小于等于其子节点的值。所以数组的第一个元素永远是最大或最小的。
二叉树中当前下标为i，左孩子为2i+1，右孩子为2i+2。

2.堆的插入

每次插入都是将新数据放到数组的最后一个，前一部分是有序的堆，所以要解决的问题是将一个元素插入到一个有序的序列中。

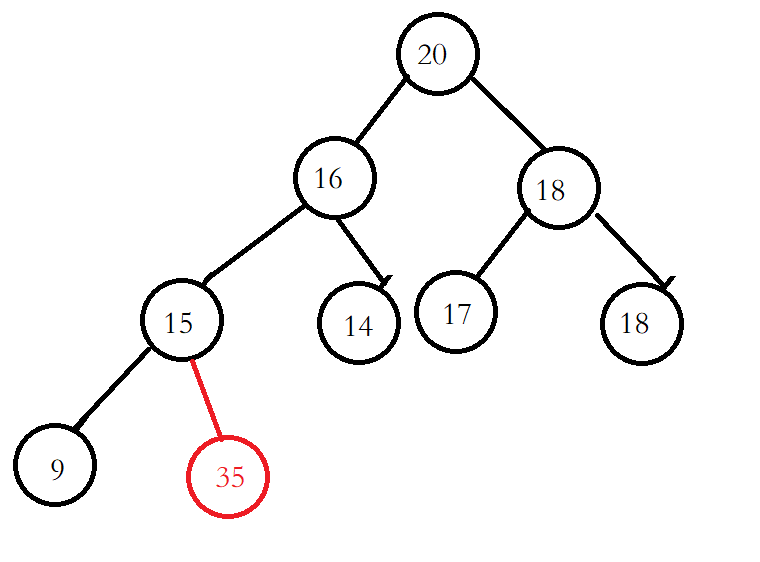
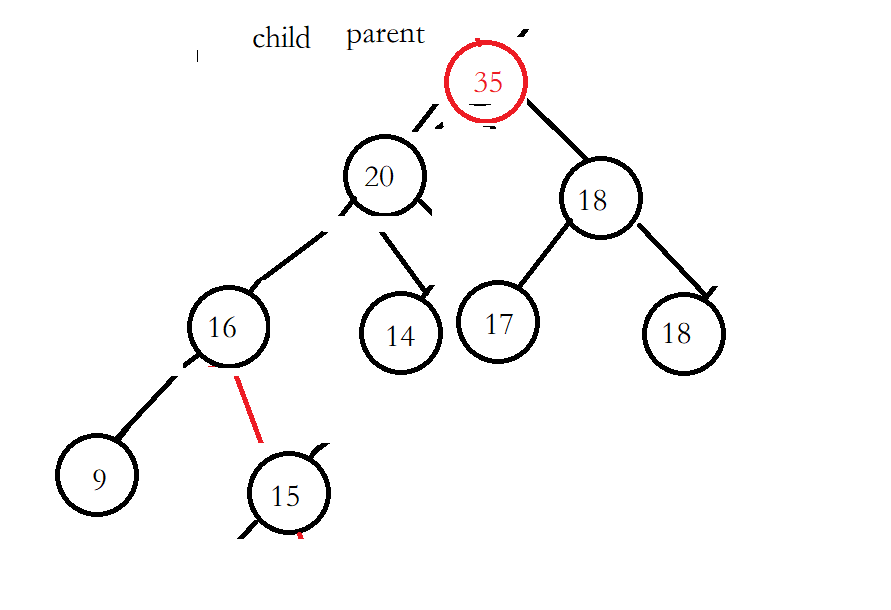
这个堆的原始数组是[20,16,18,15,14,17,18,9]，要把35插入到堆首先把35放到数组尾部。
数组就变成了[20,16,18,15,14,17,18,9,35]。

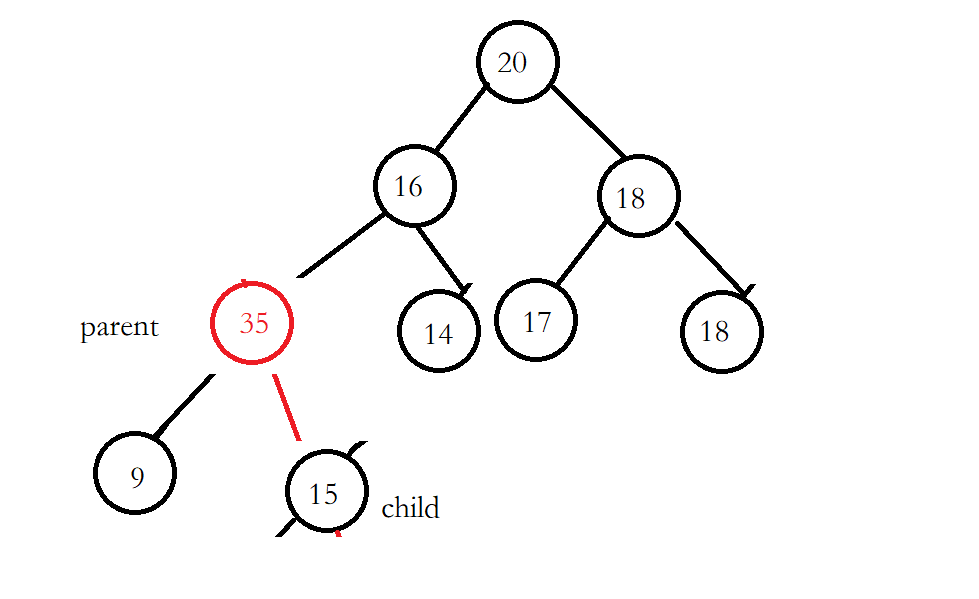
然后将35与他的父节点进行比较，看看插入后是否满足堆的特点(孩子比父亲小或者大)，这个堆是大堆，所以孩子必须比父亲小，但是35比15大所以需要交换。孩子的下标是size-1是已知的。父亲的下标=(孩子的下标-1)/2.

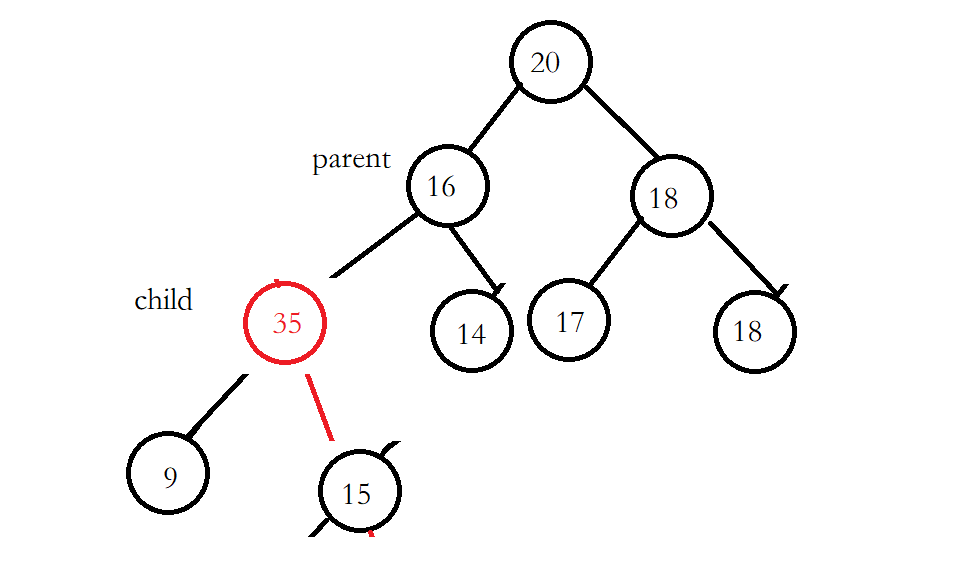
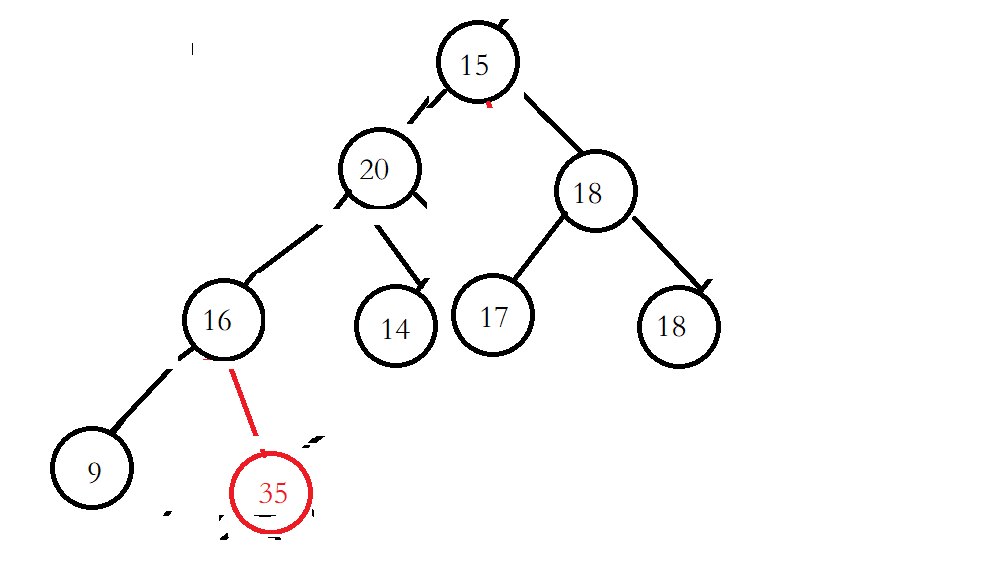
交换完成之后更新parent和child

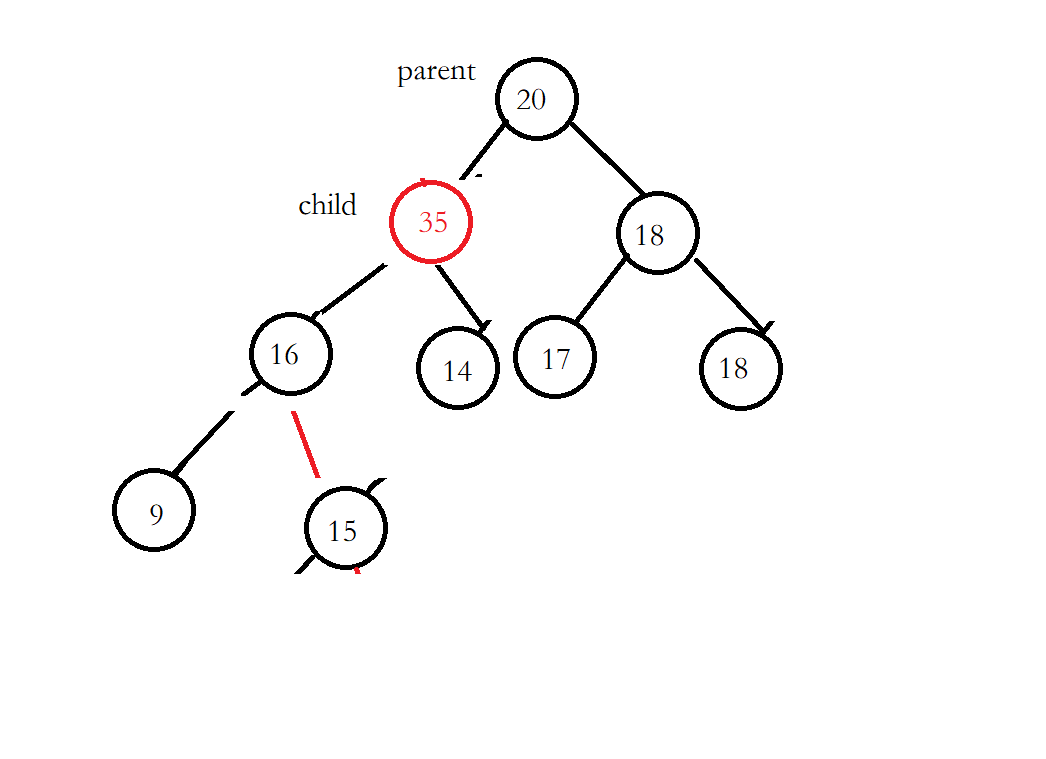
继续进行向上调整

调整完成后数组的元素为[35,20,18,16,14,17,18,9,15]

3.堆的删除

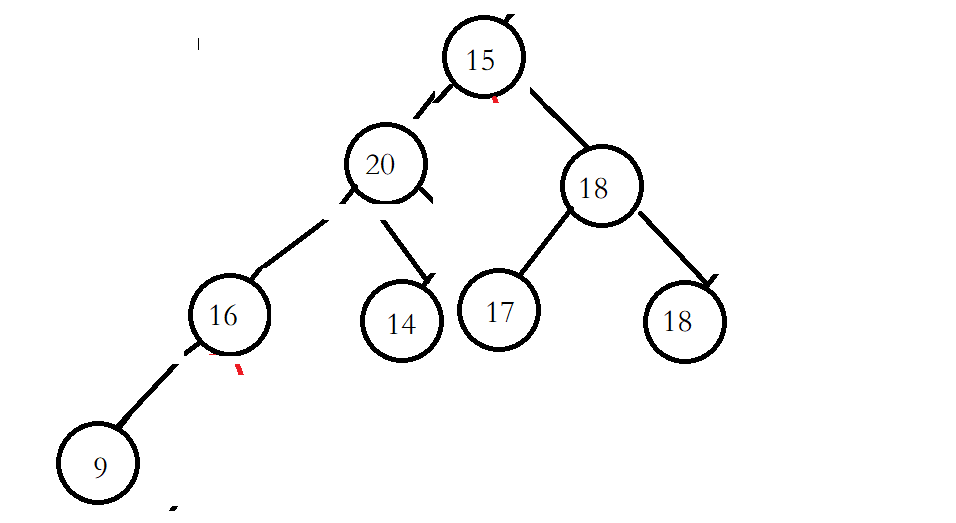
堆的删除是默认删除堆顶也就是最大或最小的元素。如果直接向前覆盖的话，会导致树的所有结构混乱。所以删除采用的是将头节点和最后一个节点交换位置

删除最后一个节点的元素

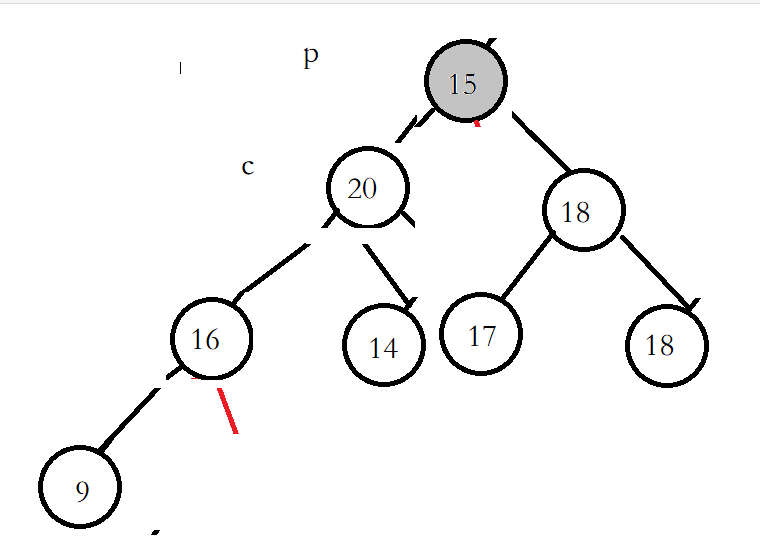
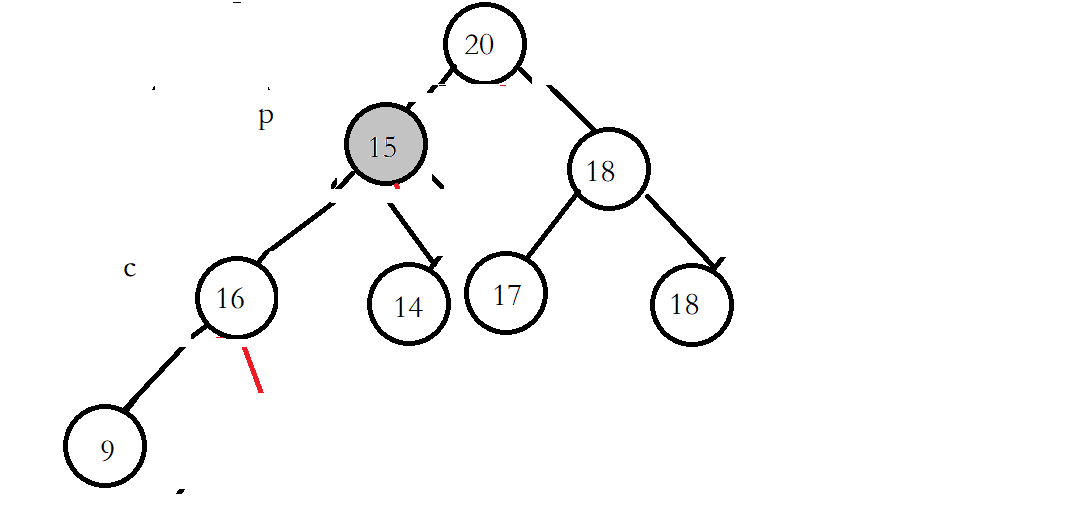
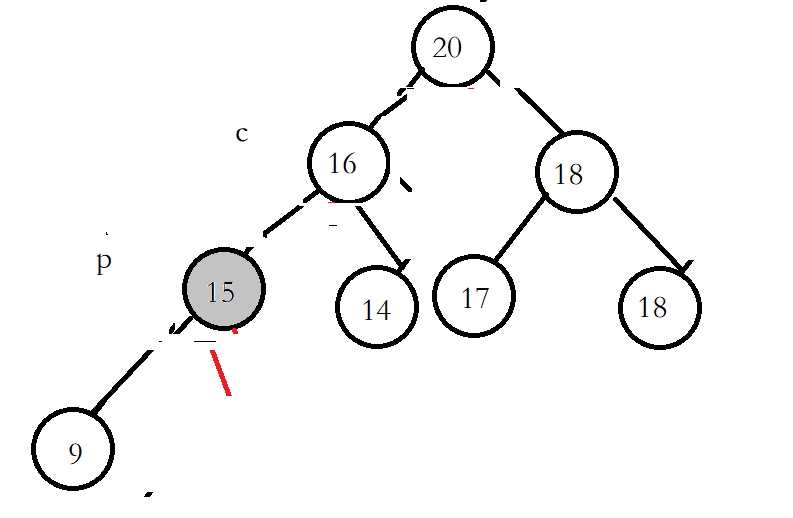
由于头节点已经改变，所以需要调整头节点的位置，头节点下的左右子树位置没有改变，所以可以将头节点向下调整。将头节点和两个子节点进行比较，如果最大的子节点比头节点大，就可以进行交换。然后向下持续这个逻辑，直到子节点超出节点个数。

左节点是子节点中最大的且大于头节点，进行交换，将p和c指针向下循环

继续进行交换

最后不小于p的子节点结束，或者c遍历到数组长度外也结束。

#pragma once
#include
#include
#include
typedef int HPDataType;
typedef struct Heap
{
	HPDataType* _a;
	int _size;
	int _capacity;
}Heap;

// 堆的构建
void HeapCreate(Heap* hp, HPDataType* a, int n);
// 堆的销毁
void HeapDestory(Heap* hp);
// 堆的插入
void HeapPush(Heap* hp, HPDataType x);
// 堆的删除
void HeapPop(Heap* hp);
// 取堆顶的数据
HPDataType HeapTop(Heap* hp);
// 堆的数据个数
int HeapSize(Heap* hp);
// 堆的判空
int HeapEmpty(Heap* hp);
//堆的调整
void HeapAdjust(Heap* hp);
void HeapAdjustToDown(int* a, int n);

#include"Heap.h"
void HeapCreate(Heap* hp, HPDataType* a, int size) {
	assert(hp);
	hp->_a = NULL;
	hp->_size = 0;
	hp->_capacity = 0;
	for (size_t i = 0; i < size; i++)
	{
		HeapPush(hp, a[i]);
	}
}
void HeapDestory(Heap* hp) {
	assert(hp);
	free(hp->_a);
	hp->_size = 0;
	hp->_capacity = 0;
}
void swap(int* a, int* b) {
	int tmp = *a;
	*a = *b;
	*b = tmp;
}
void HeapAdjust(Heap* hp) {
	int child = hp->_size - 1;
	int parent = (child - 1) / 2;
	while (child>0)
	{
		if (hp->_a[child]>hp->_a[parent])
		{
			swap(hp->_a + child, hp->_a + parent);
			child = (child - 1) / 2;
			parent = (parent - 1) / 2;
		}
		else
		{
			break;
		}
	}
}
void HeapPush(Heap* hp, HPDataType x) {
	assert(hp);
	if (hp->_capacity == hp->_size)
	{
		size_t newcapacity = hp->_capacity == 0 ? 4 : hp->_capacity * 2;
		Heap* tmp = (Heap*)realloc(hp->_a, sizeof(HPDataType) * newcapacity);
		if (tmp == NULL)
		{
			perror("realloc fail");
			exit(-1);
		}
		hp->_a = tmp;
		hp->_capacity = newcapacity;
	}
	hp->_a[hp->_size++] = x;
	HeapAdjust(hp);
}
void HeapAdjustToDown(int *a,int n) {
	int parent = 0;
	int child = 2 * parent + 1;
	while (child<n)
	{
		if (child + 1 < n && a[child + 1] > a[child])child++;
		if (a[child] > a[parent])
		{
			swap(a + parent, a + child);
			parent = child;
			child = parent * 2 + 1;
		}
		else 
		{
			break;
		}

	}
	
}
void HeapPop(Heap* hp) {
	assert(hp);
	swap(hp->_a, hp->_a + hp->_size - 1);
	hp->_size--;
	HeapAdjustToDown(hp->_a, hp->_size);
}
HPDataType HeapTop(Heap* hp) {
	assert(hp && hp->_size);
	return hp->_a[0];
}
int HeapSize(Heap* hp) {
	assert(hp);
	return hp->_size;
}
int HeapEmpty(Heap* hp) {
	assert(hp);
	return hp->_size == 0;
}