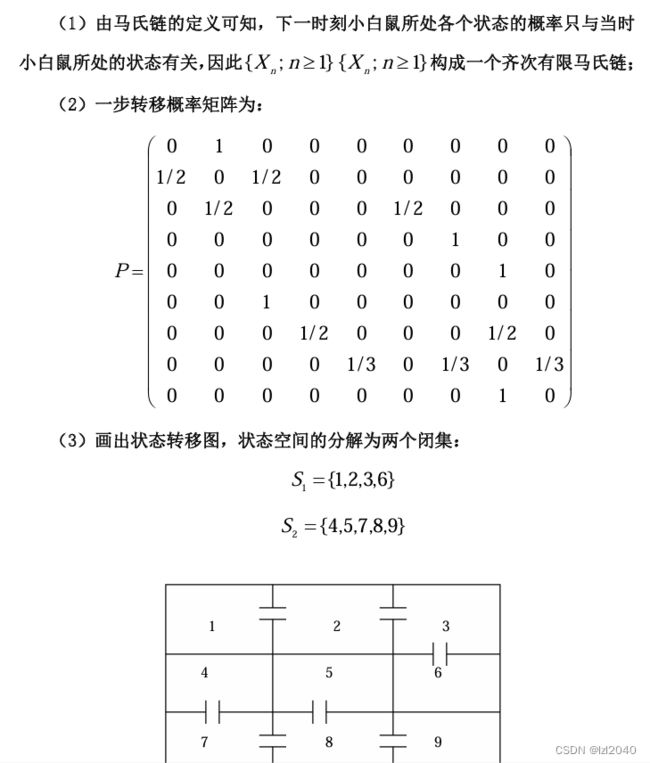
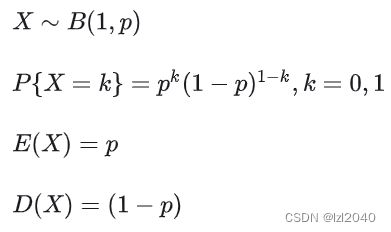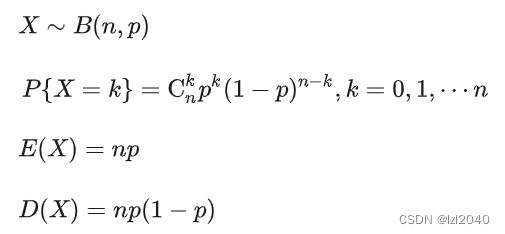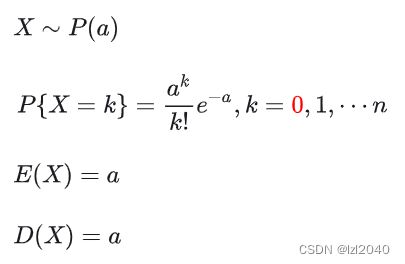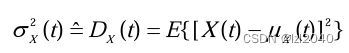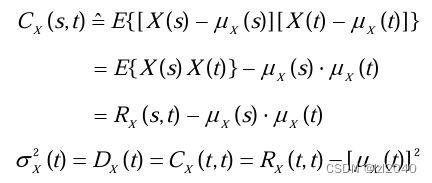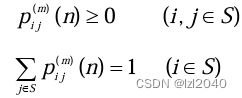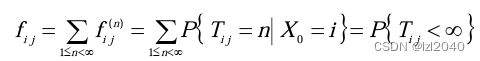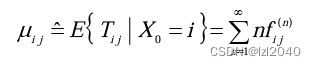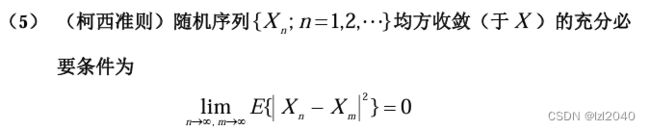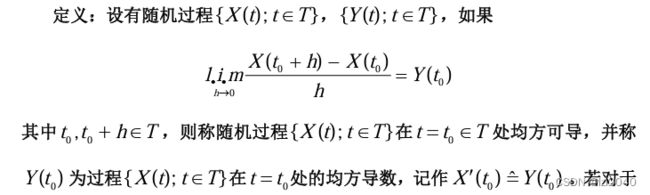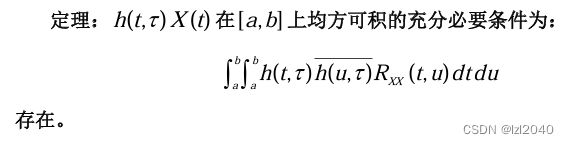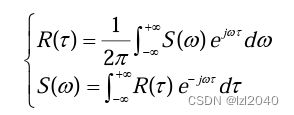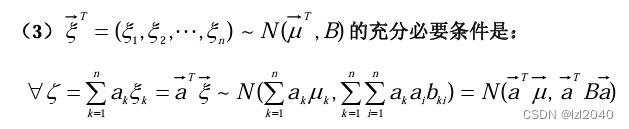【课程复习-01】国科大-随机过程知识点精简版
国科大-随机过程知识点精简版
目录
- 国科大-随机过程知识点精简版
-
- 前言
- 随机过程及其分类
-
- 常见分布的概率密度和分布
-
- 0-1分布
- 二项分布
- 泊松分布
- 几何分布
- 均匀分布
- 指数分布
- 正态分布
- 随机过程的两种描述方式
-
- 例题
- 随机过程X(t)的数字性质
-
- 单个随机过程
- 两个随机过程
- 随机过程的分类方式
-
- 参数集和状态空间的特性
- 统计特征或概率特征
- 随机过程独立
- 条件数学期望
- 马尔可夫过程
-
- 马尔可夫链定义
- C-K方程
-
- m步转移概率
- C-K方程
- 马尔可夫链状态的分类
-
- 到达和相通
- 首达时间和首达概率
- 状态的分类
-
- 例题
- 闭集和状态空间的分解
- 状态分类
- 分解定理
- 有限状态马氏链的性质
-
- 例题
- 马氏链的极限性态与平稳分布
-
- 极限性态
- 平稳分布
-
- 例题
- 非常返态分析
-
-
- 例题
-
- 泊松过程
-
- Poisson过程的一维分布
-
- 独立增量过程
- 计数过程
- Poisson过程
- Poisson过程与指数分布的关系
-
- 顺序统计量
- 到达时间的条件分布
-
- 例题
- 非齐次(时齐)Poisson过程
- 复合Poisson过程,条件Poisson过程
-
- 复合Poisson
- 条件Poisson
- 二阶矩过程,平稳过程和随机分析
-
- 二阶矩过程
-
- 定义
- 相关性质
- 平稳过程
-
- 严平稳过程
- 宽平稳随机过程
-
- 例题
- 正交增量过程
-
- 定义
- 独立增量和正交增量的关系
- X(t)为非平稳随机过程
-
- 例题
- 随机分析(针对二阶矩过程)
-
- 均方极限
- 均方连续
- 均方导数
-
- 均方可导的判定准则
- 随机积分
-
- 例题
- 平稳过程的谱分析
-
- 确定性函数(信号)的能谱分析
-
- 傅里叶变换
- 能量积分及能量谱密度
- 确定性信号的卷积与相关函数
-
- 卷积
- 相关函数
- 相关函数和能量谱密度之间的关系
- 平稳随机过程(信号)的功率谱密度
-
- 平稳随机过程功率谱密度P的定义
- 功率谱密度的性质
- 例题
- 随机信号通过线性系统后输入信号与输出信号的功率谱之间的关系
- 高斯过程
-
- 多元正态(Gauss)分布
-
- 判定正态分布
- 高斯(正态)过程
-
- 定义
- 正态过程的判定方法
- 结语
前言
孙老师的随机过程课太硬了,期末6道题没一道简单的,就前面3道会一点,博主耗尽毕生所学尽力了,希望老师别挂我。
随机过程及其分类
常见分布的概率密度和分布
0-1分布
二项分布
泊松分布
几何分布
均匀分布
指数分布
概率密度函数:
称X服从参数为θ的指数分布
分布函数:
均值: E ( x ) = λ E(x)=\lambda E(x)=λ
方差: D ( x ) = λ 2 D(x)=\lambda^2 D(x)=λ2
正态分布
随机过程的两种描述方式
- 给定参数t,即X(t,)是在样本空间上的函数,即一随机变量
- 给定w,X(,w)是关于参数t的函数,通常称为样本函数,或者是随机过程的一次实现,所有样本函数集合构成一个随机过程
例题
随机过程X(t)的数字性质
单个随机过程
两个随机过程
随机过程的分类方式
参数集和状态空间的特性
- 离散参数离散型随机过程
- 连续参数离散型随机过程
- 连续参数连续型随机过程
- 离散参数连续型随机过程
统计特征或概率特征
- 独立增量过程
- Markov过程
- 二阶矩过程
- …
随机过程独立
条件数学期望
马尔可夫过程
马尔可夫链定义

具有无后效性,随机过程将来所处各个状态的可能性只与现在随机过程所处的状态有 关,而与过去无关,称为马氏性。
一步转移概率:![]()
性质: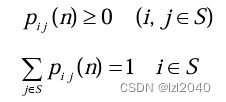
如果与时刻n无关,称此马氏链为齐次(或时齐的)马氏链

只要得到了马氏链的一步转移概率及初始分布,就可以求得马氏链的任意前n+1维的联合分布
C-K方程
m步转移概率
C-K方程
对于一般的马氏方程,有:
对于齐次马氏将时间n和n+m删除即可。
马尔可夫链状态的分类
到达和相通
首达时间和首达概率
状态的分类
-
常返态(返回态): f i i = 1 f_{ii}=1 fii=1
-
非常返态(滑过态、瞬时态): f i i < 1 f_{ii}<1 fii<1
-
对于常返态
-
正常返: μ i < ∞ \mu_i\lt \infin μi<∞
-
零常返: μ i = ∞ \mu_i = \infin μi=∞
-
若i是非常返状态,则在过程中访问它的平均次数是有限的;对于一个常返态i,在过程中访问它的次数必然是无限的
例题
闭集和状态空间的分解
- 闭集概念:设C是状态空间S的一个子集,如果从C内任何一个状态i不能到达 C外的任何状态,则称C是一个闭集。
- 所有常返态构成一个闭集
- 吸收态:单个状态i构成的集{i}是闭集,则 称状态i是吸收态,此时 p i i = 1 p_{ii}=1 pii=1
- 闭集不可约:闭集C中不再含有任何非空闭的真子集
- 当S不可约时,则 称此马氏链不可约,否则称此马氏链可约。
- 在不可约马氏链中,所有状态具有相同的状态类型
- 齐次马氏链不可约可以得到任何两个状态均互通
- 所有常返态构成一个闭集
周期的概念:
遍历态:非周期正常返状态。一个不可约的、非周期的、有限状态的马氏链一定是遍历的
状态分类

如果i和j互通,则i和j或者都是非常返态,或者都是零常返态,或者都是正常 返非周期的(遍历),或者都是正常返有周期的且有相同的周期。
分解定理

其中D是非常返态集,C是由常返状态组成的不可约集,其中的状态互通
有限状态马氏链的性质
例题
马氏链的极限性态与平稳分布
极限性态
平稳分布

![]()

非周期的不可约链是正常返的充分必要条件是它存在平稳分布,且此时平稳分布就是极限分布。
例题
非常返态分析
例题
泊松过程
Poisson过程的一维分布
独立增量过程
计数过程
- 独立增量计数过程:计数过程在不相交的时间间隔内事件A出现的次数是相互独立的
- 平稳增量计数过程:计数过程在时间间隔[t,s+t)内出现事件A的次数只与时间差s有关,而与起始时间t无关
Poisson过程
- 均值:$E[N(t)]=\lambda t $
- 二阶矩: E [ N ( t ) 2 ] = λ t + ( λ t ) 2 E[N(t)^2]=\lambda t + (\lambda t)^2 E[N(t)2]=λt+(λt)2
- 方差: D [ N ( t ) ] = λ t D[N(t)]=\lambda t D[N(t)]=λt
- 相关函数: R X ( t 1 , t 2 ) = λ 2 t 1 t 2 + λ m i n ( t 1 , t 2 ) R_X(t_1,t_2)=\lambda^2t_1t_2+\lambda min(t_1,t_2) RX(t1,t2)=λ2t1t2+λmin(t1,t2)
Poisson过程与指数分布的关系

![]()
S n S_n Sn的分布函数:
S n S_n Sn概率密度:
![]()
当n=1时,有:
顺序统计量


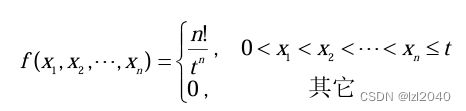


( S 1 , S 2 , . . . , S n ) (S_1,S_2,...,S_n) (S1,S2,...,Sn)的联合概率密度: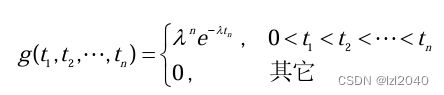
( X 1 , X 2 , . . . , X n ) (X_1,X_2,...,X_n) (X1,X2,...,Xn)的联合概率密度:

到达时间的条件分布
这部分是在 N ( t ) = n N(t)=n N(t)=n下, S 1 , S 2 , . . . , S n S_1,S_2,...,S_n S1,S2,...,Sn的条件分布问题




例题


其中 E { ∑ i = 1 n S i ∣ N ( t ) = n } E{\{\sum_{i=1}^{n}S_i | N(t)=n}\} E{∑i=1nSi∣N(t)=n}等价于 E { ∑ i = 1 n Y i } E{\{\sum_{i=1}^{n}Y_i}\} E{∑i=1nYi},其中 Y i Y_i Yi是 S i S_i Si的顺序统计量,在[0,t]均匀分布,计算过程:
E { ∑ i = 1 n Y i } = ∑ i = 1 n E ( Y i ) E ( Y i ) = ∫ 0 t y 1 t d y = t 2 ∑ i = 1 n E ( Y i ) = ∑ i = 1 n t 2 = n t 2 E{\{\sum_{i=1}^nY_i\}}=\sum_{i=1}^nE{(Y_i)} \\ E(Y_i)= \int_{0}^{t}y \frac{1}{t}dy=\frac{t}{2} \\ \sum_{i=1}^nE{(Y_i)}=\sum_{i=1}^n\frac{t}{2}=\frac{nt}{2} E{i=1∑nYi}=i=1∑nE(Yi)E(Yi)=∫0tyt1dy=2ti=1∑nE(Yi)=i=1∑n2t=2nt
非齐次(时齐)Poisson过程
复合Poisson过程,条件Poisson过程
复合Poisson
条件Poisson
二阶矩过程,平稳过程和随机分析
二阶矩过程
定义
相关性质
平稳过程
严平稳过程

严平稳随机过程的一维分布函数与时间t无关。因此,如果严平稳随 机过程的均值函数存在的话,则是一常数
严平稳随机过程的任意二维分布函数只与时间差有关。因此,如果严 平稳随机过程的二阶矩存在的话,则自相关函数只与时间差有关
宽平稳随机过程
对于严平稳随机过程,只有它二阶矩存在时,它才是宽平稳过程
例题
正交增量过程
定义
独立增量和正交增量的关系
X(t)为非平稳随机过程
例题
随机分析(针对二阶矩过程)
均方极限
均方连续

判定均方连续:
如果 X ( t ) X(t) X(t)是宽平稳过程,它等价于:
- X ( t ) X(t) X(t)均方连续
- X ( t ) X(t) X(t)在t=0处均方连续
- 自相关函数 R X X ( i ) R_{XX}(i) RXX(i)在i=0处连续
- 自相关函数 R X X ( i ) R_{XX}(i) RXX(i)在R上连续
均方导数
均方可导的判定准则
随机积分
例题
平稳过程的谱分析
确定性函数(信号)的能谱分析
傅里叶变换

F ( ω ) F(\omega) F(ω)也称为为确定性信号 f ( t ) f(t) f(t)的 频谱函数,它的模称为 f ( t ) f(t) f(t)的振幅频谱,简称频谱

能量积分及能量谱密度
确定性信号的卷积与相关函数
卷积
相关函数
相关函数和能量谱密度之间的关系
平稳随机过程(信号)的功率谱密度
平稳随机过程功率谱密度P的定义
功率谱密度的性质

对于零均值的随机过程,有:
上面就是Wienner-Khinchine定理:任意零均值的平稳过程的功率谱和它的自相关函数组成一对Fourier变 换对

均值为零,功率谱密度为非零常数的平稳随机过程(信号)称为白噪声
例题
随机信号通过线性系统后输入信号与输出信号的功率谱之间的关系
高斯过程
多元正态(Gauss)分布
判定正态分布
高斯(正态)过程
定义
正态过程的判定方法
原始过程是正态过程,现在的过程可以写成原始过程的线性变换形式,则它是正态过程。

结语
希望考试顺利!