【论文阅读】ControlNet、文章作者 github 上的 discussions
文章目录
- Introduction
- Method
-
- ControlNet
- ControlNet for Text-to-Image Diffusion
- Training
- Inference
- Experiments
-
- 消融实验
- 定量分析
- 在作者 github 上的一些讨论
-
- 消融实验更进一步的探索
- Precomputed ControlNet 加快模型推理
- 迁移控制能力到其他 SD1.X 模型上
- 其他
Introduction
- 提出
ControlNet,通过引入该结构微调预训练文生图扩散模型,可以给模型增加空间定位条件. - 在
Stable Diffusion上使用ControlNet微调,使模型能接受 Canny edges, Hough lines, user scribbles, human key points, segmentation maps, shape normals, depths, cartoon line drawings 图像作为输入条件. - 消融实验、定量分析、对比 baseline.
Method
ControlNet
考虑一个预训练好的神经网络 F ( ⋅ ; Θ ) \mathcal{F}(·;\Theta) F(⋅;Θ)表示训练好的神经网络块,它的内部结构可以包括 resnet, conv-bn-relu, muti-head att, transfomer 等. 输入 x ∈ R h × w × c x\in\mathbb{R}^{h\times w\times c} x∈Rh×w×c,将其转换到 y y y,也即
y = F ( x ; Θ ) \large y=\mathcal{F}(x;\Theta) y=F(x;Θ)
使用ControlNet微调神经网络 F ( ⋅ ; Θ ) \mathcal{F}(·;\Theta) F(⋅;Θ),首先复制 F ( ⋅ ; Θ ) \mathcal{F}(·;\Theta) F(⋅;Θ)的结构和参数,参数命名为 Θ c \Theta_{c} Θc,同时冻结 Θ \Theta Θ. 然后在复制结构的前和后分别引入zero convolution,也即核大小为 1 × 1 1\times1 1×1、初始参数为 0 0 0的卷积层,分别用 Z ( ⋅ ; Θ z 1 ) \mathcal{Z}(·;\Theta_{z1}) Z(⋅;Θz1)和 Z ( ⋅ ; Θ z 2 ) \mathcal{Z}(·;\Theta_{z2}) Z(⋅;Θz2)表示. 最后,将 c c c作为微调时的条件,将其整合到模型的前向计算中,具体表示为
y c = F ( x ; Θ ) + Z ( F ( x + Z ( c ; Θ z 1 ) ; Θ c ) ; Θ z 2 ) \large y_c=\mathcal{F}(x;\Theta)+\mathcal{Z}(\mathcal{F}(x+\mathcal{Z}(c;\Theta_{z1});\Theta_c);\Theta_{z2}) yc=F(x;Θ)+Z(F(x+Z(c;Θz1);Θc);Θz2)
在训练的第一步中,zero convolution的参数都为 0 0 0,因此模型输出和未加入ControlNet的输出一样,这样做有助于在刚开始训练时保护微调结构的 backbone,使其免受随机噪声的污染.
ControlNet for Text-to-Image Diffusion
众所周知,Stable Diffusion训练时的网络有这么几个部分构成:
- FrozenCLIPEmbedder是一个预训练的 text encoder,将 prompt 嵌入成条件向量,一般情况下参数冻结.
- AutoencoderKL是一个预训练的 image encoder,将图像从像素空间转换到隐空间,降低扩散过程中图像向量的尺寸,一般情况下参数冻结.
- UNet,主要需要训练的部分,模拟隐空间上图像在数据分布和高斯分布之间转换的过程. 结构上主要包含:
- 若干 encoder 块,主要由 resnet, transformer, avg_pool 组成,用于逐层提取特征.
- resnet 块融合图像隐向量和扩散时间步的嵌入向量
- transformer 块融合图像隐向量和 prompt 条件向量
- 一个 middle 块,由 resnet 和 transformer 组成
- 若干 decoder 块,主要由 resnet, transformer, interpolate 组成,用于融合深层特征和浅层特征.
- 若干 encoder 块,主要由 resnet, transformer, avg_pool 组成,用于逐层提取特征.
将ControlNet应用于Stable Diffusion做微调,也即应用于其中UNet的 decoder 部分,使这部分网络能进一步融合作为条件的图像。用 t t t表示时间步, c t c_t ct表示 prompt 条件, c f c_f cf表示条件图像在隐空间上的表示,修改后的UNet结构为
Training
用 z 0 z_0 z0表示原始图像的隐向量,经过时间步 t t t后加噪的图像表示为 z t z_t zt,应用了ControlNet的UNet表示为 ϵ θ \epsilon_{\theta} ϵθ,训练时的损失函数可以表示为
L = E z 0 , t , c t , c f , ϵ ∈ N ( 0 , I ) [ ∣ ∣ ϵ − ϵ θ ( z t , t , c t , c f ) ∣ ∣ 2 2 ] \large \mathcal{L}=\mathbb{E}_{ z_0,t,c_t,c_f,\epsilon\in\mathcal{N}(0,I)}\left[||\epsilon-\epsilon_{\theta}(z_t,t,c_t,c_f)||_2^2\right] L=Ez0,t,ct,cf,ϵ∈N(0,I)[∣∣ϵ−ϵθ(zt,t,ct,cf)∣∣22]
在实际训练过程中,作者随机将 50 % 50\% 50%的 prompt 置为空字符串,这种做法能使ControlNet学习到图像条件的语义信息. 由于zero convolution不会引入额外的噪声,因此在训练过程中整个Stable Diffusion模型仍然能生成高质量的图片. 基于这一特性,作者观察到,微调时模型并非逐渐学习到图像条件,而是在训练步数低于 10 K 10\mathrm{K} 10K时的某一步开始突然遵从图像条件. 作者称这其为 “sudden convergence phenomenon”

Inference
Stable Diffusion使用CFG控制条件强弱,令 ϵ u c \epsilon_{uc} ϵuc表示无 prompt 条件的模型输出, ϵ c \epsilon_{c} ϵc表示有 prompt 条件的模型输出,超参数 β c f g \beta_{cfg} βcfg表示 prompt 条件的强弱,模型最终的输出 ϵ p r d \epsilon_{prd} ϵprd可以表示为
ϵ p r d = ϵ u c + β c f g ( ϵ c − ϵ u c ) \large \epsilon_{\mathrm{prd}}=\epsilon_{\mathrm{uc}}+\beta_{\mathrm{cfg}}(\epsilon_{\mathrm{c}}-\epsilon_{\mathrm{uc}}) ϵprd=ϵuc+βcfg(ϵc−ϵuc)
在没有 prompt 条件的极端情况下,如果抽取完深层特征的图像条件同时加到 ϵ u c \epsilon_{uc} ϵuc和 ϵ c \epsilon_{c} ϵc上,这会使CFG完全失去控制条件强弱的作用;如果只加到 ϵ c \epsilon_{c} ϵc上,又会使控制条件对输出图像的影响过大. 因此,作者提出一种叫做Classifier-free guidance resolution weighting(CFG-RW)的方法. 具体做法,把图像条件加到 ϵ c \epsilon_{c} ϵc上,在ControlNet每一层输出加回UNet前乘系数 w i w_i wi( = 64 / h i =64/h_i =64/hi, h i h_i hi为第 i i i个 decoder 块的尺寸). 下图分别展示了该讨论各种情况下的输出图像:

有了上述方法之后,结合不同类别的图像条件,也只需要对应相加即可.
Experiments
消融实验
探索ControlNet其他可能结构
- 将
zero convolution换成随机初始化的卷积层 - 只使用一个卷积层作为
ControlNet
定量分析
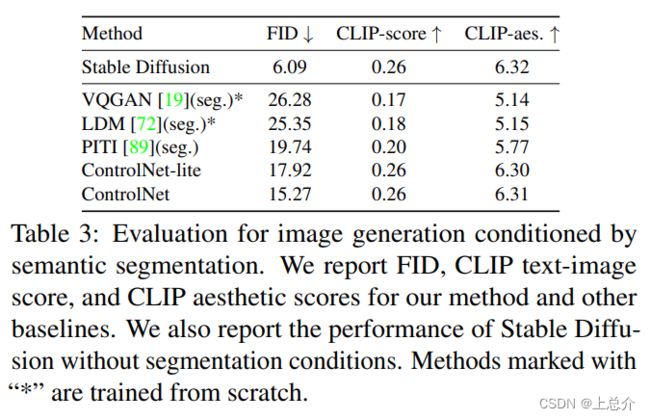
作者使用 ADE20K 作为测试集,在 OneFormer 上做语义分割,对比不同方法重构图像和原图像的 IoU .

之后,作者评估了不同模型的 FID、CLIP score、CLIP aesthetic score.
在作者 github 上的一些讨论
消融实验更进一步的探索
discussion 链接
将ControlNet简化为ControlNet-lite和ControlNet-mlp两种模型:

作者从根据一张房子的图片做了简单地涂鸦风格处理,作为控制条件

|

|
在精心设计 prompt 的情况下,发现原版模型和改后的两种模型输出的图像效果都不错.
Professional high-quality wide-angle digital art of a house designed by frank lloyd wright. A delightful winter scene. photorealistic, epic fantasy, dramatic lighting, cinematic, extremely high detail, cinematic lighting, trending on artstation, cgsociety, realistic rendering of Unreal Engine 5, 8k, 4k, HQ, wallpaper
|
|
|
|
但是当 prompt 为空时,两种改版都很拉胯.
|
|
|
|
一方面,这样的对比说明更深的 encoder 结构确实拥有更强的识别能力,所以如果你的目标是训练稳健的ControlNet投入到生产环境,这样的识别能力是很重要的. 反之,如果用来做解决特定问题的研究或者训练集足够简单,那可以考虑轻量化的方案.
另一方面,这也解释了ControlNet接受 prompt 条件和时间步输入是重要的,因为这么做可以让使用者仍然能靠 prompt 条件调整模型的输出.
Precomputed ControlNet 加快模型推理
这样做可以提前计算好ControlNet中每个块的输出,在推理时直接加到原模型的UNet上.
作者观察到这样训练的模型生成的图像更假,并且更不稳健,以失败告终.
评论中有人提到可以尝试使用 NAS (neural architecture search) 探索更好的模型结构,以降低 GPU 消耗.
迁移控制能力到其他 SD1.X 模型上
discussion 链接
作者尝试将在 Stable Diffusion 1.5上训练的ControlNet迁移到AnythingV3上,作者给出的方法是:
AnythingV3_control_openpose = AnythingV3 + SD15_control_openpose – SD15
限制有两点:
- text encoder 不同会导致意外结果
- 在例如 human pose 的应用中,输入最好不是二刺螈人物图片,因为检测姿势用的 OpenPose 不擅长处理二刺螈人物.
这种方法已经过时了. 目前在实际应用中,直接把ControlNet插到其他 SD1.X 模型上就行.
其他
- Riffusion + ControlNet 音乐修复
- 将原图转换成像素风格
- 人物换衣
- 调色