初阶数据结构:顺序表相关题目练习
顺序表相关题目练习
- 一,引子
- 二, 练习题目
-
- 1. 移除指定元素
- 2. 删除有序数组中的重复项
- 3. 合并两个有序数组
一,引子
在对顺序表这一数据结构进行了学习与自实现后,我明白了顺序表的是使用了物理地址上连续的数组模型实现的,而插入删除的操作都会涉及到其中数据的挪动与边界问题。接下来,就结合算法时空间复杂的要求来对这一相关问题通过几道题目进行巩固练习。
二, 练习题目
1. 移除指定元素
- 数组nums
- 数组长度numsSize
- 移除元素值val
题目链接:
题目:移除元素
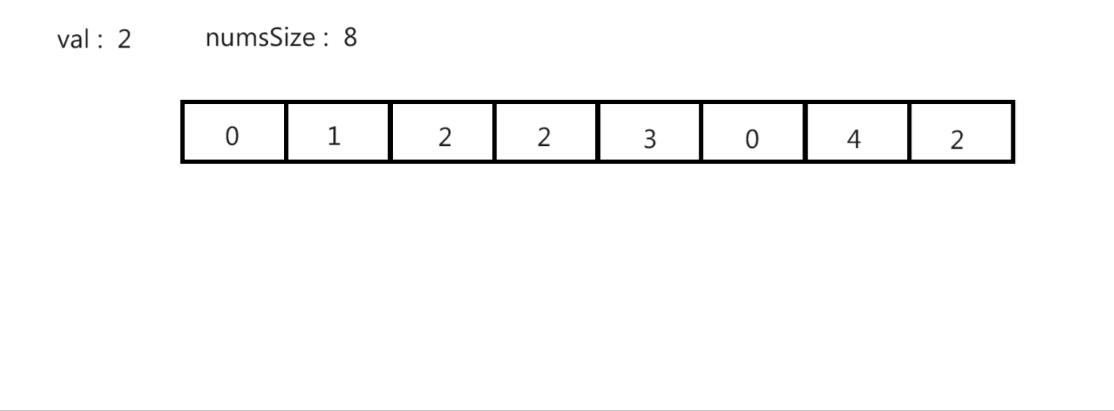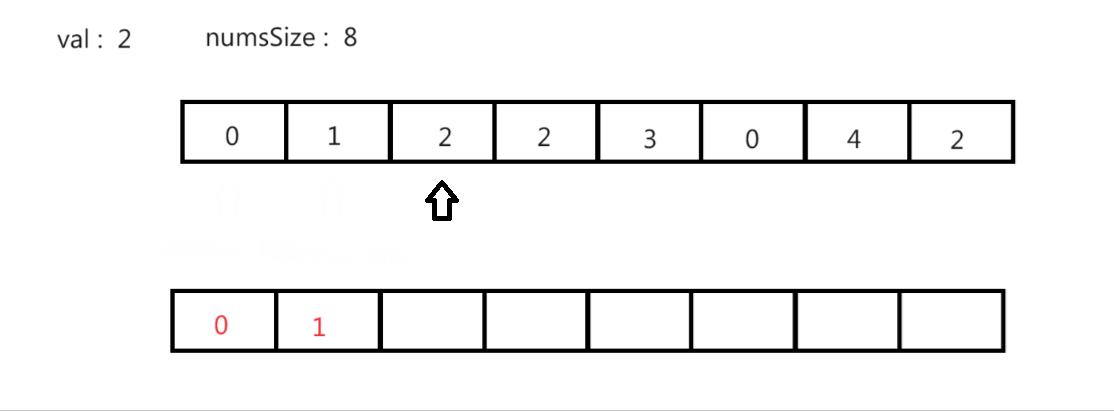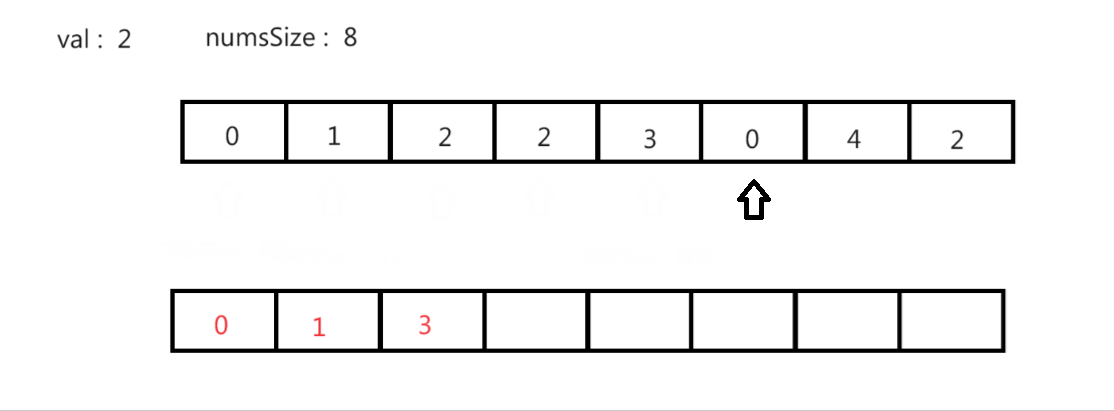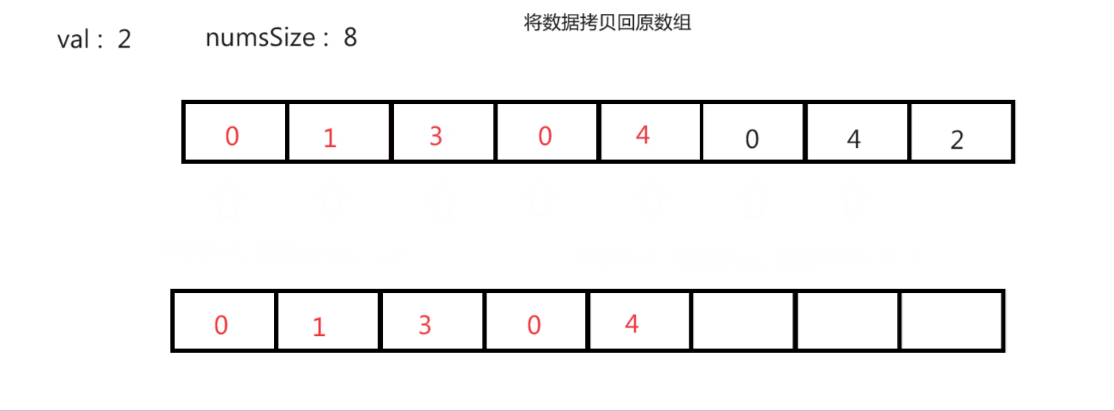
方法1(空间换时间):
思路(时间复杂度 O(n) 空间复杂度 O(n)):开辟一块相同大小的空间,将原数组中不等于val的值拷贝进新空间内。遍历完成后,将新空间中的数据再拷贝回原数组中。
int removeElement1(int* nums, int numsSize, int val)
{
//开辟新空间
int* arr = (int*)malloc(numsSize * sizeof(int));
int i = 0;
int j = 0;
//将不等于val的值复制至新空间内
for (i = 0; i < numsSize; i++)
{
if (nums[i] != val)
{
arr[j] = nums[i];
j++;
}
}
//将数据拷贝会原数组
memcpy(nums, arr, (j * sizeof(int)));
//释放申请的新空间
free(arr);
return j;
}
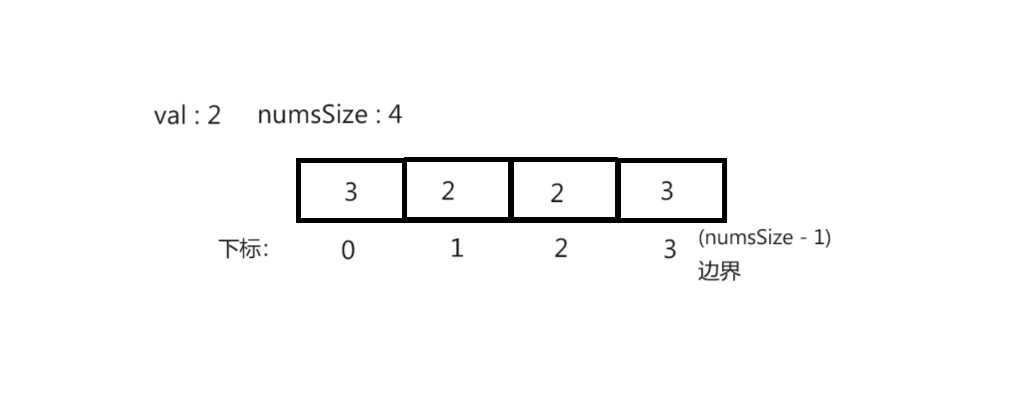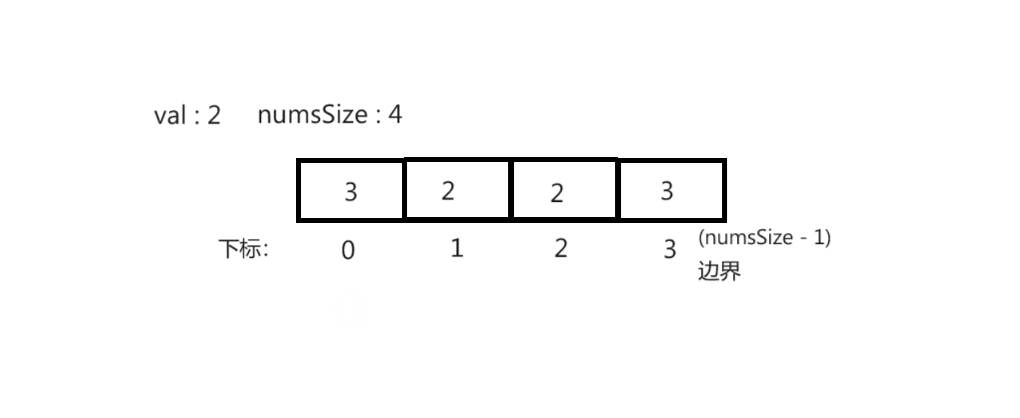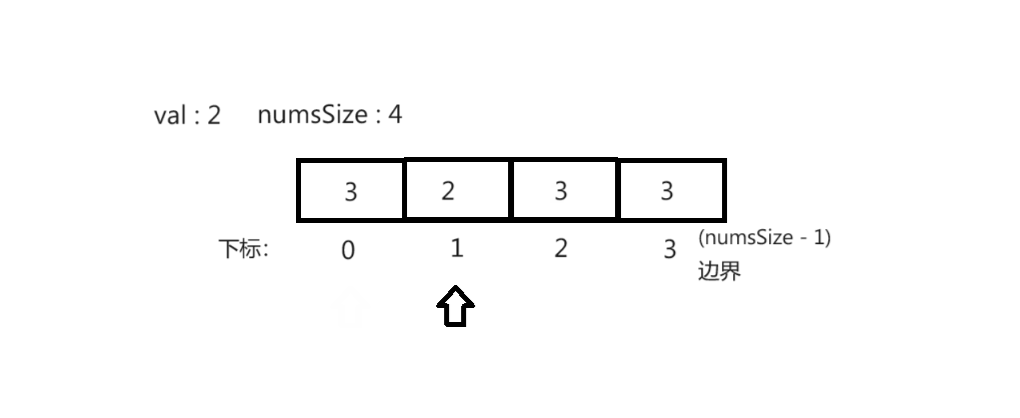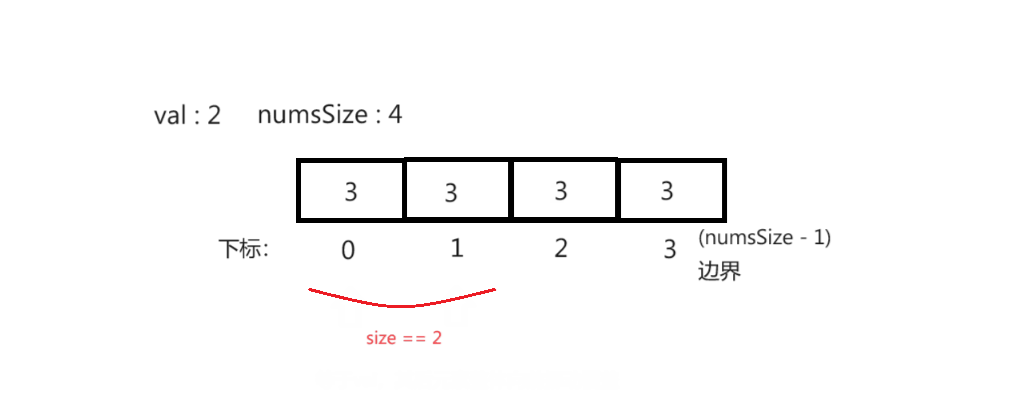
方法2(挪动覆盖元素):
思路(时间复杂度 O(n^2) 空间复杂度 O(1)):遍历数组,若数组元素等于val,将数组后面元素整体前移覆盖,若不等于下标加1。
int removeElement2(int* nums, int numsSize, int val)
{
//原地挪动覆盖
//时间复杂度O(n^2),空间复杂度O(1)
int len = numsSize;
int i = 0;
while (i < len)
{
if (nums[i] == val)
{
int j = i;
while (j < len - 1)
{
nums[j] = nums[j + 1];
j++;
}
len--;
}
else
{
i++;
}
}
return len;
}
2. 删除有序数组中的重复项
- 数组nums
- 数组长度numsSize
- 数组为非严格递增序列(不递减)
题目链接:
题目:删除重复项
方法1(空间换时间):
思路(时间复杂度 O(n) 空间复杂度 O(n)):开辟等大小空间,将每个元素拷贝一份到新空间中,最后全部拷贝回去。
int removeDuplicates1(int* nums, int numsSize)
{
//额外空间拷贝
int* arr = (int*)malloc(numsSize * sizeof(int));
int i = 0;
int j = 0;
while (i < numsSize)
{
if (i + 1 >= numsSize || nums[i] != nums[i + 1])
{
arr[j] = nums[i];
j++;
}
i++;
}
memcpy(nums, arr, j * sizeof(int));
free(arr);
return j;
}
方法2(挪移覆盖):
思路(时间复杂度 O(n^2) 空间复杂度 O(1)):将重复出现的元素使用数组后续元素挪移覆盖。
int removeDuplicates2(int* nums, int numsSize)
{
//非严格递增排列
//暴力求解挪移
//O(n^2)
int i = 0;
int len = numsSize;
while (i < len - 1)
{
if (nums[i] == nums[i + 1])
{
int j = i;
while (j < len - 1)
{
nums[j] = nums[j + 1];
j++;
}
len--;
}
else
{
i++;
}
}
return len;
}
3. 合并两个有序数组
- 两个数组:nums1,nums2
- 两数组中分别的元素个数:m,n
- 两数组容量:numsSize1,numsSize2
- 两数列都为非严格递增序列
- 最后合并数据存放在数组nums1
题目链接:
题目:合并两个有序数组
方法1(从前向后比较,需要额外空间):
注:从前向后往nums1数组中拷贝数据会对原数据产生覆盖,所以需要开辟新空间。
void merge1(int* nums1, int nums1Size, int m, int* nums2, int nums2Size, int n)
{
int* cp_num = (int*)malloc((m + n) * sizeof(int));
int* long_num = nums1;
if (nums1Size < nums2Size)
{
long_num = nums2;
}
int i = 0;
int j = 0;
int x = 0;
while (i < m || j < n)
{
//nums2为空数组
if (j == n || (i < m && nums1[i] <= nums2[j]))
{
cp_num[x] = nums1[i];
i++;
}
else
{
cp_num[x] = nums2[j];
j++;
}
x++;
}
memcpy(long_num, cp_num, (m + n) * sizeof(int));
}
方法2(从后向前比较):
从后比较,自后向前拷贝数据,不会产生数据的覆盖,直接拷贝到nums1中。
void merge2(int* nums1, int nums1Size, int m, int* nums2, int nums2Size, int n)
{
//非递减顺序
//1. 比大小,将较小的元素放入大数组中(从前往后)
//2. 将较大的元素放入大数组中(从后往前)
int* long_num = nums1;
if (nums1Size < nums2Size)
{
long_num = nums2;
}
int end1 = m - 1;
int end2 = n - 1;
int insert = m + n - 1;
while (end1 >= 0 || end2 >= 0)
{
//特殊情况,有一个数组插入完成
//nums1插入完,nums2插入完
if ((end2 < 0) || (end1 >= 0 && nums1[end1] >= nums2[end2]))
{
long_num[insert] = nums1[end1];
end1--;
}
else
{
long_num[insert] = nums2[end2];
end2--;
}
insert--;
}
}
方法2(改):
注:(优化)当nums2中的元素插入完成,nums1没有插入完成无,需再进行插入操作,数组中数据本就有序。
void merge3(int* nums1, int nums1Size, int m, int* nums2, int nums2Size, int n)
{
int end1 = m - 1;
int end2 = n - 1;
int end = m + n - 1;
//固定为nums1存放合并后的数组
while (end1 >= 0 && end2 >= 0)
{
if (nums1[end1] >= nums2[end2])
{
nums1[end--] = nums1[end1--];
}
else
{
nums1[end--] = nums2[end2--];
}
}
//nums1中的元素未遍历完,nums1的剩余元素本就有序,无需再插入
while (end2 >= 0)
{
nums1[end--] = nums2[end2--];
}
}