非递归实现归并排序

目录

非递归的归并排序

---

非递归的归并排序

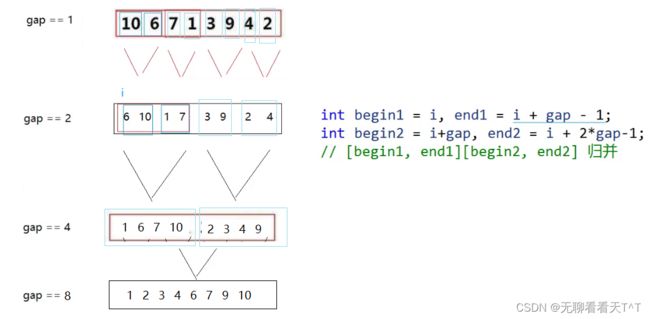
1、像递归实现归并排序一样，开辟n个空间大小的临时数组

2、gap表示归并时的每组数据的个数

3、while循环实现成对归并，每轮归并排序完之后（while循环结束，gap = gap*2为下一次更大范围的归并做准备），且gap应小于原数组本身的数据个数之和n（不能越界）

4、内嵌for循环实现单趟归并，i表示每次要归并的数组首元素的下标，初始值为0（当我们将10和6归并排序完成后，7和1进行归并排序）此时i的值应该发生变化（开始第二次for循环）i = i + gap * 2，即i在原来的基础上加上每次归并的数组元素个数*2（当gap==1时，第一次单趟归并的是下标为0的10和下标为1的6，第二次单趟归并的是下标为2的7和下表为3的1...；当gap==2时，第一次单趟归并的是下标为0的6、下标为1的10和下标为2的1、下标为3的7，第二次归并的是......；当gap==3时，单趟归并的是整个数组） 每一轮归并i的最大取值范围与gap有关

//非递归递归排序
void MergeSortNonR(int* a, int n)
{
	int* tmp = (int*)malloc(sizeof(int) * n);
	if (tmp == NULL)
	{
		perror("malloc fail");
		return;
	}

	int gap = 1;//gap用于表示归并时的每组数据的个数
	while (gap < n)
	{
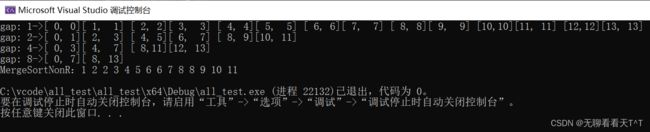
		printf("gap:%2d->", gap);
		for (size_t i = 0; i < n; i += 2 * gap)
		{
			int begin1 = i, end1 = i + gap - 1;
			int begin2 = i + gap, end2 = i + 2 * gap - 1;
			int j = begin1;
			while (begin1 <= end1 && begin2 <= end2)
			{
				if (a[begin1] < a[begin2])
				{
					tmp[j++] = a[begin1++];
				}
				else
				{
					tmp[j++] = a[begin2++];
				}
			}

			while (begin1 <= end1)
			{
				tmp[j++] = a[begin1++];
			}

			while (begin2 <= end2)
			{
				tmp[j++] = a[begin2++];
			}

			memcpy(a + i, tmp + i, sizeof(int) * (end2 - i + 1));
		}

		printf("\n");

		gap *= 2;
	}


	free(tmp);
}

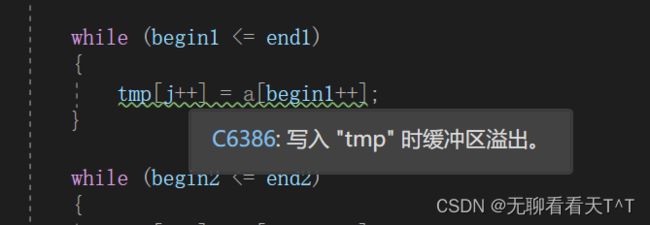
6、当我们处理数组{10，8，7，1，3，9，4，2}时，上述代码并不会出错，但是当我们处理数组{10，8，7，1，3，9，4，2，9，10}时系统就会提示栈溢出：

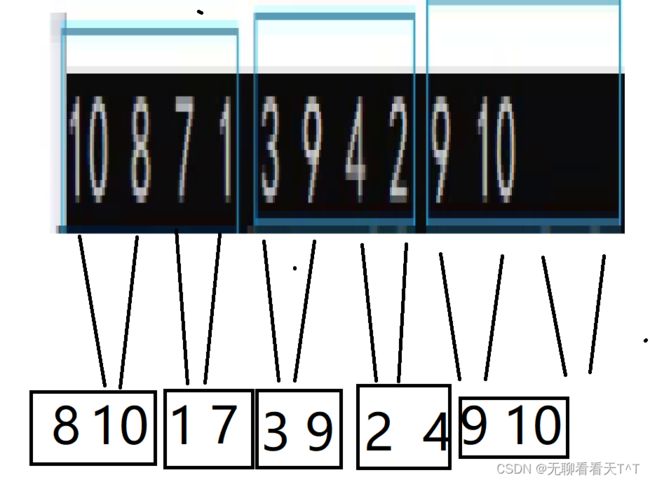
7、这是因为实际的数组元素个数不一定成恰当的倍数变大（八个数组元素时可以刚好满足需求，十六个数组元素时也刚好可以满足需求，但是其他情况呢？），每轮归并（while循环），i（数组元素下标）的最大取值范围虽然会一直小于n，但是begin1、begin2、end1、end2这些与i相关的变量的值可能在原数组下标中根本不存在（它们可能会大于原数组尾元素下标值，就比如下图中的gap==1时，十个元素可以刚好即第一轮归并排序各项内容正常，但是当gap==2时，第三趟的归并排序其实只有下标8的9和下标为9的10，但是实际上begin1 = 8 end1 = 9、begin2 = 10 end2 = 11明显超出了原数组尾元素下标的值9，当超出数组范围时，访问到的内存位置可能不属于当前数组，如下图所示a[9]就是最大了，怎么可能有a[10]，然后还让a[8]判断与a[10]的大小）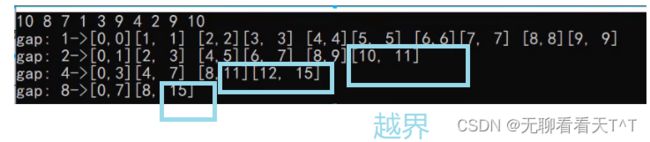

在归并操作时如果没有进行边界处理判断和调整，可能会导致以下问题：

1. 越界访问：如果第一组或第二组超出了数组的索引范围，则在读取或写入数据时会越界访问到不属于当前数组的内存位置。这将导致程序崩溃、段错误等运行时错误。

2. 归并错误：当越界发生时，很可能无法正确地执行归并操作。例如，在合并两个子序列之前需要比较它们的元素大小，并按顺序放入临时数组中。但是由于越界问题，无法得知实际应该比较哪些元素以及如何正确地放置它们。

3. 错误结果：由于缺少边界处理而产生上述问题后，排序算法将无法得到正确结果。排序后得到的数组可能包含错误顺序、重复元素或丢失部分元素等问题

处理前：

处理后：

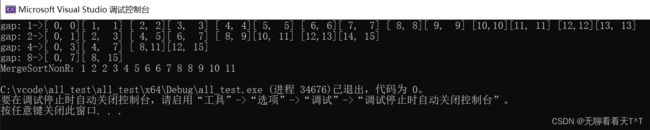
7、所以为了应对数组越界，我们还需要进行边界处理的操作，即当end1大于等于n（end1等于n，后面begin2肯定越界）或者begin2大于等于n时（begin2等于n，后面的end2肯定越界）应该结束此次循环，证明此时后面的已经没有有效数据需要进行归并了

8、当end2大于等于n时（此时可能还有数组的尾元素可能还需要进行归并，就剩它一个了），应end2的值进行修正，让它的大小重新回到正常n-1（end2每次的值都应该是原数组末尾元素的下标） 

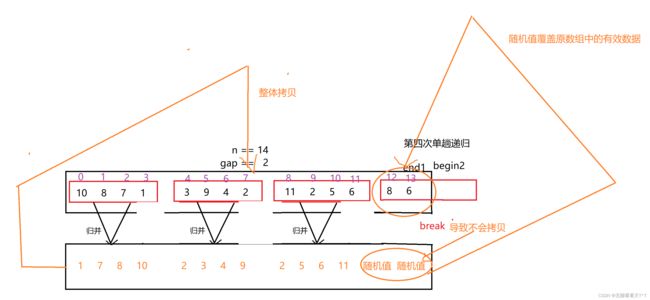
9、每一轮的单趟归并后就需要进行memcpy函数，而不是一轮的所有单趟归并都结束后才进行memcpy（memcpy放在for循环中）如果一轮拷贝一次，就会导致临时数组中末尾的位置可能出现因为break没有将原数组的有效数据归并进临时数组，故末尾位置上的数据为随机值，在最后将一轮归并后的tmp数组重新拷贝回原数组就会出现随机值覆盖原数组末尾未参与归并的有效数据：

//非递归递归排序
void MergeSortNonR(int* a, int n)
{
	int* tmp = (int*)malloc(sizeof(int) * n);
	if (tmp == NULL)
	{
		perror("malloc fail");
		return;
	}

	int gap = 1;//gap用于表示归并时的每组数据的个数
	while (gap < n)
	{
		printf("gap:%2d->", gap);
		for (size_t i = 0; i < n; i += 2 * gap)
		{
			int begin1 = i, end1 = i + gap - 1;
			int begin2 = i + gap, end2 = i + 2 * gap - 1;
			// [begin1, end1][begin2, end2] 归并
			//printf("[%2d,%2d][%2d, %2d] ", begin1, end1, begin2, end2);  //边界处理前的数组范围

			// 边界的处理
			if (end1 >= n || begin2 >= n)
			{
				break;
			}

			if (end2 >= n)
			{
				end2 = n - 1;
			}

			//printf("[%2d,%2d][%2d, %2d] ", begin1, end1, begin2, end2);  //边界处理后的数组范围

			int j = begin1;
			while (begin1 <= end1 && begin2 <= end2)
			{
				if (a[begin1] < a[begin2])
				{
					tmp[j++] = a[begin1++];
				}
				else
				{
					tmp[j++] = a[begin2++];
				}
			}

			while (begin1 <= end1)
			{
				tmp[j++] = a[begin1++];
			}

			while (begin2 <= end2)
			{
				tmp[j++] = a[begin2++];
			}

			memcpy(a + i, tmp + i, sizeof(int) * (end2 - i + 1));
		}

		printf("\n");

		gap *= 2;
	}


	free(tmp);
}

~over~