【算法深入浅出】字符串匹配之 KMP 算法
KMP 算法是一种字符串匹配算法。字符串匹配算法的目标是:在字符串 s 中找到与模式串 p 相等的子串,输出其位置。例如:s = “abcdef”,p = “cdef”,p 在 s 中的位置是 2(从 0 开始计数)。
int findString(string s, string p) {
int n = s.size(), m = p.size();
int i, j;
for (i = 0; i < n - m + 1; i++) {
for (j = 0; j < m; j++) {
if (s[i + j] == s[j]) continue;
break;
}
if (j == m) return i;
}
return -1;
}
暴力算法的最坏情况下,时间复杂度是 O ( n m ) O(nm) O(nm)。而本文尝试要讲明白的 kmp 算法,他的摊还时间复杂度是 O ( n ) O(n) O(n) 的。
kmp 算法执行速度要快不少,但是也是有代价的:也就是出了名的难理解。但我认为,只要 提纲挈领的找到 kmp 算法的主干,那还是比较好理解的,也就 2 分钟的事吧。算法实现上会有一些坑,这才是最难的地方,需要将里面的思路捋顺,但花些时间总能搞出来。那我们就开始吧。
从直觉开始
假设有这样一个样例:s = “bacbababababcbab”,p = “ababaca”。算法运行到如下位置,s 的索引为 9,p 的索引为 5 时匹配错误了。

暴力算法会将 s 移进 1 字符,然后重新从 s 的 5 号字符和 p 的 0 号字符开始匹配。相当于 s 的索引从 9 回退到 5,p 的索引从 5 回退到 0。
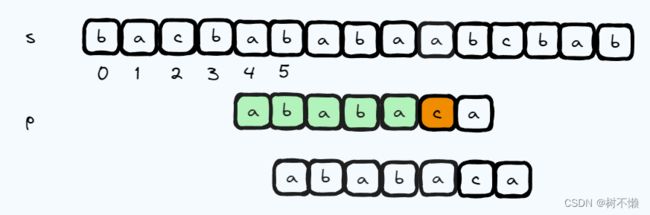
而 kmp 算法就比较聪明一些。既然 p 字符串的 0 到 4 号字符都匹配成功了,我们何不利用这个信息,多向前移动几个字符呢。怎么做呢? kmp 算法的思想如下:到目前位置,已经成功匹配了 p 的前缀中 " a b a b a " "ababa" "ababa" 这个字符串。然后我们同时考虑它的 前缀 和 后缀,会发现

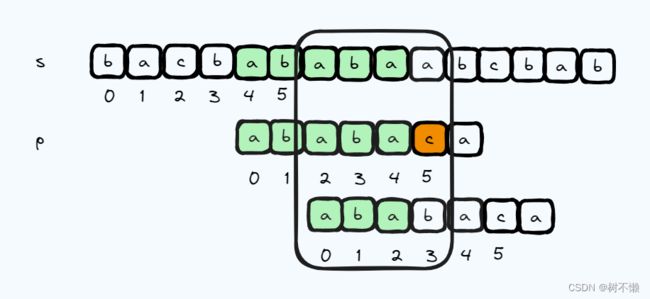
它的前三个字符和后三个字符是完全一样的。所以我们完全可以向下图一样,从 s 的 9 号 字符和 p 的 3 号字符开始匹配,相当于 s 的索引没有回退,p 的索引从 5 回退到 3。这可比暴力匹配回退的少多了,因此也就快多了。
至此 kmp 算法的思想就讲完了。上述思想,如果不考虑如何实现的话,可能最多 2 分钟就可以理解。
但是想要实现它却又不知该怎么下手,那我们就一点一点的拆解它。
next 数组引入
next 数组,往往又叫前缀函数。我们不整那么高深的东西,就为了解决一个问题:p 的索引该回退到哪? 根据上面的分析,s 的索引是没有回退的,那么 p 的索引该回退到哪里呢?这个问题需要再精确一些:如果 p 在 索引 i 的位置匹配失败了,那么 p 的索引该回退到哪里?这就是 next 数组的作用:索引应该回退到 next[i] 的位置。
为了不使代码复杂化,我们先假设,如果已经得到了 next 数组,算法框架是什么样的呢?
- 版本1(错误):
int findString(string s, string p) {
int n = s.size(), m = p.size();
int i, j = 0;
for (i = 0; i < n;) {
if (s[i] == p[j]) { // 如果相等,i 和 j 都进 1
i++, j++;
} else { // 如果不相等,i 保持不变,j 变为 next[j]
j = next[j];
}
// 如果 j == m 表示 s 在 i 处匹配完成了,返回 i - m;
if (j == m) return i - m;
}
return -1;
}
根据版本 1 的注释,看起来好像没什么问题,但不幸的是,它有 bug。j = next[j] 这一行没有处理边界情况:即当 s[i] 不等于 s[j],并且,当 j == 0 的情况,此时意味着 0 号位置也匹配失败了,这时候 next[j] 应该等于多少呢?答案是:还是 0。为什么呢?因为即使 0 号位置匹配失败了,下一次要变化的应该是要把 s 的索引加 1 才对,而 p 的索引依旧是 0。于是有了下面的代码版本。
plus. 有一些别的 kmp 算法版本 定义为 -1。实际上是把整个 next 数组做了一次变换,只要改一下 next 数组的定义即可。我们学会一个就好了。主要是另一个我没想通。。
- 版本2.1
int findString(string s, string p) {
int n = s.size(), m = p.size();
int i, j = 0, flag = 0;
for (i = 0; i < n;) {
if (s[i] == p[j]) { // 如果相等,i 和 j 都进 1
i++, j++;
} else { // 如果不相等,i 保持不变,j 变为 next[j]
j = next[j];
if (flag == 1) {
flag = 0;
i++;
} else if (j == 0) flag = 1;
}
// 如果 j == m 表示 s 在 i 处匹配完成了,返回 i - m + 1;
if (j == m) return i - m;
}
return -1;
}
版本2.1是一个正确的版本,但是不够优雅。作为一个程序员,要有一定的审美,版本 2.1 本质上是用单层循环模拟了多层循环,如果能够拆出来,就更好了。
版本2.2
int n = s.size(), m = p.size();
int i, j = 0;
for (i = 0; i < n; i++) {
// 如果不相等,i 保持不变,j 变为 next[j]
while (j != 0 && s[i] != p[j]) {
j = next[j];
}
if (s[i] == p[j]) { // 如果相等,j 进 1
j++;
}
// 如果 j == m 表示 s 在 i 处匹配完成了,返回 i - m + 1;
if (j == m) return i - m + 1;
}
return -1;
}
嗯,版本2.2 就优雅许多了。
next 数组生成
那么 next 数组该如何生成呢?

对照这幅图,当 p 的 5 号索引匹配失败是,j 应该跳转到 3 号。可以观察到,next[i] 表示 [0, i - 1] 区间表示的字符串 p i p_i pi 中 重叠的前缀与后缀的最长值 k,并且 k 要小于 p i p_i pi 的长度,因为自己等于自己可不算。
plus. 这句话要反复琢磨,写的不好但是确实很重要,决定了能不能正确实现。
所以算法如下
vector next(m, 0);
for (int i = 2; i < m; i++) { // 前两个数字默认为 0
int t = next[i - 1]; // 前面的前面的那个区间有最长多少个重叠的前后缀
// 前面的区间末尾 和 前面的前面的区间的末尾如果不相等就一直 next
// 这点和匹配算法很像
while (t != 0 && p[i - 1] != p[t]) {
t = next[t];
}
if (p[i - 1] == p[t]) t++; //如果相等就 +1
next[i] = t;
}
合成如下
int strStr(string s, string p) {
int n = s.size(), m = p.size();
// 求 next 数组
vector next(m, 0);
for (int i = 2; i < m; i++) {
int t = next[i - 1];
while (p[i - 1] != p[t] && t != 0) t = next[t];
if (p[i - 1] == p[t]) t++;
next[i] = t;
}
// 匹配
int j = 0;
for (int i = 0; i < n; i++) {
while (s[i] != p[j] && j != 0) j = next[j];
if (s[i] == p[j]) j++;
if (j == m) return i - m + 1;
}
return -1;
}
总结
kmp 算法思想就是使用已匹配的前缀字符串,从中抽取出前后缀的重叠部分信息,用以减少字符串匹配中的回退,从而达到加速的作用。其实现有两个坑,一个是next 数组含义的准确定义(我的定义应该和书上不一样),第二个坑就是使用内循环来多次使用 next 数组跳转。其中第二个坑相信大家自己写都能意识到,第一个坑才是决定你能不能写出来的关键因素。我的实现可能不是最好的,但是希望能够好懂一点。
kmp 算法已将前缀信息使用到了极致,还有一些别的字符串比较算法要比 kmp 容易一些,比如 sunday 算法等。还有一些算法可能比 kmp 还要复杂一些,使用到了后缀信息,例如:bm 算法。还有 一个 RK 算法使用哈希字符串的方式,简单易写。这些算法有机会再说吧。
