姿势的搬运工

【步进电机 stepping motor】二梯形加减速

前言：

声明：学习笔记来自正点原子B站教程，仅供学习交流！！

1. 梯形加减速算法概述

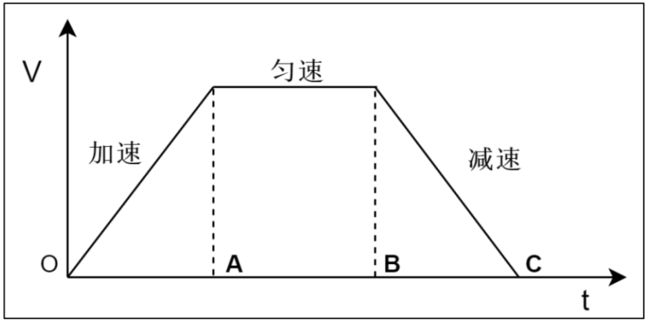
梯形加减速一共分为三个阶段，OA 加速部分、AB 匀速部分和 BC 减速部分。在 OA 加速过程中，由低于步进电机的启动频率开始启动（模型中由 0 启动），以固定的加速度增加速度到目标值；在 AB 匀速过程中，以最大速度匀速运动；在 BC 减速部分中，以加速度不变的速度递减到 0；这种算法是一种在加速过程和减速过程中加速度不变的匀变速控制算法，由于速度变化的曲线有折点，所以在启动、停止、匀速段中很容易产生冲击和振动

2. 算法基础

2.1 脉冲时间间隔的精确计算

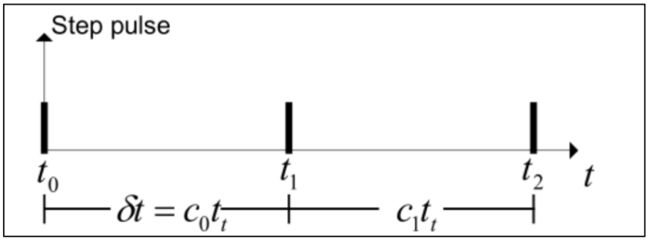
步进电机的转动需要控制器发送脉冲，如果控制器以恒定速度发送脉冲，那么步进电机就以恒定速度转动；如果控制器以加速度发送脉冲，那么步进电机就以加速度运动；所以只要改变脉冲的频率就可以改变速度的变化，也就是说调整脉冲之间的时间间隔就可以改变速度。

$t_{0}$ 表示第1个脉冲发送时刻
$t_{1}$ 表示第2个脉冲发送时刻
$t_{2}$ 表示第3个脉冲发送时刻
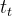$t_{t}$ 表示定时器的计数周期
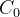$C_{0}$ 表示定时器从 $t_{0}$ ~ $t_{1}$ 时刻的定时器计数值
$C_{1}$ 表示定时器从 $t_{1}$ ~ $t_{2}$ 时刻的定时器计数值
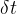$\delta t$ 表示两个脉冲之间的间隔时间

以 stm32 的高级定时器 8 为例，使用定时器PWM输出模式给控制器发送脉冲。高级定时器 8 的时钟频率为 168MHZ, 如果将分频值设置为 5，那么定时器的时钟频率则为: $f_{t}$ =168/(5+1)=28MHZ, 相当于计数 28M 次正好为一秒，周期与频率为倒数关系，所以分频值为 5 的定时器 8 的计数周期 $t_{t} = 1/f_{t}$ ； $C_{0}$ 和 $C_{1}$ 的值即为ARR寄存器的值，所以我们在固定的定时器频率下，只需要改变ARR的值，即可改变电机的速度。

2.2 公式推导

1. 电机转过的角度θ的计算：

$\theta = n*\alpha$ （1）

$S = v_{0}t + \frac{1}{2}at^{^{2}} \rightarrow \theta = w_{0}t + \frac{1}{2}\dot{w_{0}}t^{^{2}}$ （2）

n表示驱动电机的脉冲数，α表示电机的步距角， $\theta$ 为转过的角度 , $w{_{0}}$ 为初角速度，ώ为加角速度，t为所用的时间，

一般情况下，初角速度都为0，所以得到电机转过θ所用的时间 $t_{n}$ ：

$t _{n}= \sqrt{\frac{2*\theta }{\dot{w}}}$ （3）

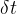
2. 间隔时间 $\delta t$

$\delta t = C_{n}*t_{t} = t_{n} - t_{n - 1}$ （4）

结合公式（3）和公式（4），可得出：

$C_{n} = \frac{1}{t_{t}}\sqrt{\frac{2\alpha}{\dot{w}} }(\sqrt{n+1} -\sqrt{n})$ （5）

上式中n表示转过 $\theta_{n-1}$ 角度时，所用的脉冲数

3. 求加减速阶段第n个周期内计数器的值

即令公式（5）的参数n = 0，即

$C_{0} = \frac{1}{t_{t}}\sqrt{\frac{2\alpha }{\dot{w}}}$ （6）

将公式（6）带入公式（5），即

$C_{n} = C_{0}(\sqrt{n + 1} - \sqrt{n})$ （7）根据泰勒公式的一个特例麦克劳林公式：

将上面公式代入公式（7），即：

最终化简得出以下公式：

$C_{n} = C_{n - 1} - \frac{2C_{n - 1}}{4n + 1}$ （8）

通过公式（8）和公式（6）即可推到出每个周期内的计时器的值，及每步的频率。经过化简的公式（8）有一定的误差，其得出的结果比公式（7）快。所以我们对公式（6）乘以0.676加以校正

$C_{0} = 0.676 * \frac{1}{t_{t}}\sqrt{\frac{2\alpha }{\dot{w}}}$ （9）

通过公式（8）和公式（9），我们就可以知道电机加速每一步的PWM频率

4. 求匀速阶段计数器的值

$w = \frac{\alpha}{\delta t}$ （10）

其中为角速度， $\alpha$ 为步距角， $\delta t$ 为间隔时间

将公式（10）带入公式（4），即

$C = \frac{\alpha f_{t}}{w}$ (11)

通过公式（11），我们就可以知道电机匀速时的PWM频率

5. 脉冲数和加速度成反比

将公式（1）带入公式（2）：

$t _{n}= \sqrt{\frac{2\alpha *n }{\dot{w}}}$ （12）

3. 梯形加减速的计算过程

我们通过控制定时器输出PWM波形来描绘上述梯形，至少需要知道以下变量：

1. 加速阶段

加速初始PWM频率，即我们要求的ARR寄存器的值 $C_{0}$
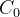
加速度accel
加速阶段时需要多少脉冲数，以n1表示

2. 匀速阶段

匀速所需要的脉冲数
匀速阶段的PWM频率

3. 减速阶段

减速阶段需要的脉冲数量
减速度decel

3.1 三角形运动

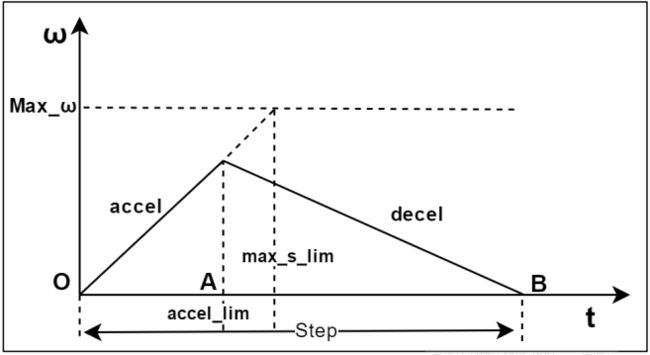
三角形运动是由于速度偏大，而加速度偏小，导致在加速阶段速度没有达到最大值而进入匀速阶段时，就必须进入减速阶段的情况

上图中，已知参数：

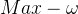$Max-\omega$ ：用户设置的最大速度
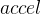：加速度大小
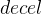：减速度大小
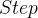：位移总步数

未知量：

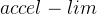：加速度曲线与减速度曲线的交点
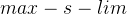：加速度一共需要的步数
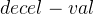：减速度所需要的步数

从上图可以看出，三角形运动没有匀速阶段，加速度过了即减速阶段，当 < 时，运动模型即为三角形运动

1. 计算加速度步数

从上图可以看出，加速度的末速度与减速度的是相等的，所以：

$\dot{w1}*t1 = \dot{w2}*t2$ （13）

其中， $\dot{w1}$ 为加速度，为加速度时间， $\dot{w2}$ 为减速度，为减速度时间

将公式（13）带入公式（12）：

$\dot{w1}*n1 = \dot{w2}*n2$ （14）

两边同时加上 $\dot{w2}*n1$ 后，化简得到：

$\dot{w1}*n1 + \dot{w2}*n1 = \dot{w2}*n2 + \dot{w2}*n1$

$(\dot{w1} + \dot{w2})*n1 = \dot{w2}*(n2 + n1)$

$n1 = \frac{\dot{w2}*(n1 + n2))}{\dot{w1} + \dot{w2}}$ （15）

又因为此时为三角形运动，所以为总步数，可以求出加速度步数

2. 计算减速度步数

（16）

3.2 梯形运动

如果加速度设置的足够大，那么在进入减速阶段之前达到最大速度，那么则会进行一段时间的匀速运动，运动图形如下：

上图中，已知参数：

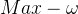$Max-\omega$ ：用户设置的最大速度
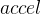：加速度大小
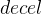：减速度大小
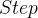：位移总步数

未知量：

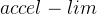：加速度曲线与减速度曲线的交点
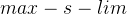：加速度一共需要的步数
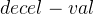：减速度所需要的步数

从上图可以看出，梯形运动中，是先进行匀减速，之后进入匀速阶段，最后进行匀减速的运动，当 > 时，运动模型即为梯形运动

1. 计算加速度步数

梯形公式，最大速度即为 $max-\omega$ ，带入公式（1）和（2），即为

$\partial n = \frac{1}{2}*\dot{w}^{2}t$

$\partial n = \frac{w^{2}}{2\dot{w}}$

$n = \frac{w^{2}}{2\partial\dot{w}}$

$n1 = \frac{max_w^{2}}{2\partial\dot{w}}$ （17）

其中，n即为加速度步数，即为 $max-\omega$ ， $\alpha$ 为电机步距角， $\dot{w}$ 为加速度

2. 计算减速不步数

将公式（17）带入公式（14）

$n2 = -n1*\frac{\dot{w1}}{\dot{w2}}$ （18）

4. 算法优化

由于算法在计算过程中涉及到一些浮点型运算，大量的浮点型运算会使得效率大大降低，为了使得计算速度得到更好的优化，我们做如下优化：

对于加减速的每一步来说，都需要重新计算下一步的时间，计算的过程中可能会出现除不尽的项式，为了更有利的加减速，可以采用加速向上取整，减速向下取整的原则来做运算，也可以采用余数累计的方法，在这里使用的是将余数累计的方法来提高间隔时间的精度和准确性。

$C_{n} = C_{n - 1} - \frac{2C_{n-1} - rest}{4n+1}$ （19）

求余公式：

$New-Rest = (2*C_{n - 1} + Rest)(mod(4*n+1))$ （20）

5. 实现步骤

在给定步距角α、定时器频率 $f_{t}$ ，加速度 $\dot{w1}$ ，减速度 $\dot{w2}$ ，最大速度，总步数Step的情况下：

匀加速阶段

1. 判断三角形运动还是梯形运动：

$accel-lim = n1 = \frac{\dot{w2}*(n1 + n2))}{\dot{w1} + \dot{w2}}$

$max-s-lim = \frac{max-w^{2}}{2\dot{w1*\alpha }}$

如果 < 则为三角形运动，则减速步数：

否则则为梯形运动，则减速步数

$n2 = -n1*\frac{\dot{w1}}{\dot{w2}}$

2. 求加速度第一步的定时器值，即 $C{_{0}}$ ：

$C_{0} = 0.676 * \frac{1}{t_{t}}\sqrt{\frac{2\alpha }{\dot{w}}}$

3. 加速阶段每步定时器的值

$C_{n} = C_{n - 1} - \frac{2C_{n-1} - rest}{4n+1}$

$New-Rest = (2*C_{n - 1} + Rest)(mod(4*n+1))$

匀速阶段

加速阶段的最大速度运行

匀减速阶段

1. 判断每步定时器值

$C_{n} = C_{n - 1} - \frac{2C_{n-1} - rest}{4n+1}$

$New-Rest = (2*C_{n - 1} + Rest)(mod(4*n+1))$

你可能感兴趣的:(电机专题,单片机,嵌入式硬件)

扫地机类清洁产品之直流无刷电机控制悟空胆好小清洁服务机器人单片机人工智能
扫地机类清洁产品之直流无刷电机控制1.1前言扫地机产品有很多的电机控制，滚刷电机1个，边刷电机1-2个，清水泵电机，风机一个，部分中高端产品支持抹布功能，也就是存在抹布盘电机，还有追觅科沃斯石头等边刷抬升电机，滚刷抬升电机等的，这些电机有直流有刷电机，直接无刷电机，步进电机，电磁阀，挪动泵等不同类型。电机的原理，驱动控制方式也不行。接下来一段时间的几个文章会作个专题分析分享。直流有刷电机会自动持续
FPGA复位专题---（3）上电复位？ FPGA系统设计指南针 FPGA系统设计(内训)fpga开发
（3）上电复位？1目录（a）FPGA简介（b）Verilog简介（c）复位简介（d）上电复位？（e）结束1FPGA简介（a）FPGA（FieldProgrammableGateArray）是在PAL（可编程阵列逻辑）、GAL（通用阵列逻辑）等可编程器件的基础上进一步发展的产物。它是作为专用集成电路（ASIC）领域中的一种半定制电路而出现的，既解决了定制电路的不足，又克服了原有可编程器件门电路数有限
基于STM32与Qt的自动平衡机器人：从控制到人机交互的的详细设计流程极客小张 stm32 qt 机器人物联网人机交互毕业设计 c语言
一、项目概述目标和用途本项目旨在开发一款基于STM32控制的自动平衡机器人，结合步进电机和陀螺仪传感器，实现对平衡机器人的精确控制。该机器人可以用于教育、科研、娱乐等多个领域，帮助用户了解自动控制、机器人运动学等相关知识。技术栈关键词STM32单片机步进电机陀螺仪传感器AD采集电路Qt人机界面实时数据监控二、系统架构系统架构设计本项目的系统架构设计包括以下主要组件：控制单元:STM32单片机传感器
以研发创新为驱动力，黄山谷捷助力新能源汽车产业高质量发展 L913197600 黄山谷捷制造科技
在新能源汽车产业蓬勃发展的浪潮中，车规级功率半导体作为驱动电机控制系统的核心部件，其性能与稳定性直接关系到汽车的动力输出、能效转化及安全性能。在这一关键领域，黄山谷捷股份有限公司（以下简称“黄山谷捷”或“公司”）以卓越的研发实力、精湛的生产工艺和严格的质量控制体系，成为行业内的佼佼者，特别是在功率半导体散热基板领域，更是树立了新的标杆。自2012年成立以来，黄山谷捷便深谙“科技是第一生产力”的真谛
AUTO TECH 2025 广州国际汽车软件与安全技术展览会 ws201907 汽车安全
AUTOTECH2025广州国际汽车软件与安全技术展览会ChinaGuangzhouSoftware-DefinedVehicleExpo2025亚洲领先的汽车软件与安全技术专业展会——是与来自世界各地的汽车工程师们交流的最佳平台！广州国际汽车软件与安全技术展览会是AUTOTECH2025华南展专题展之一，汇集了各种汽车嵌入式软件开发与应用、车载操作系统、智驾功能安全与SOTIF、基础软件平台、车
51单片机——I2C总线存储器24C02的应用老侯（Old monkey） 51单片机嵌入式硬件单片机
目标实现功能单片机先向24C02写入256个字节的数据，再从24C02中一次读取2个字节的数据、并在数码管上动态显示，直至读完24C02中256个字节的数据。1.I2C总线简介I2C总线有两根双向的信号线，一根是数据线SDA,另一根是时钟线SCL。I2C总线通过上拉电阻接正电源，因此，当总线空闲时为高电平。2.I2C通信协议起始信号、停止信号由主机发出。在数据传送时，当时钟线为高电平时，数据线上的
嵌入式单片机中数码管基本实现方法嵌入式开发星球单片机项目实战操作之优秀单片机
1.点亮数码管本节课利用已经学习的LED知识去控制一个8位数码管。本节的原理比较简单。不需要多少时间讲。更多时间是跟大家一起编码调试，从中学习一些编码思路和学习方法。1.1.什么是数码管数码管是什么？下图就是一个数码管从硬件上个看，其实就是8个LED组合在一起。8个LED应该有16个引脚，但是数码管上只有10个引脚。为什么呢？请看下图：1个LED有两个引脚，要控制LED，1个引脚接控制信号，另外一
2022-08-15 梁亦冕
当好“答卷人”，考出“好成绩”近日，习近平总书记在省部级主要领导干部“学习习近平总书记重要讲话精神，迎接党的二十大”专题研讨班上发表重要讲话时强调，高举中国特色社会主义伟大旗帜，奋力谱写全面建设社会主义现代化国家崭新篇章。此次重要讲话明确宣示党在新征程上举什么旗、走什么路、以什么样的精神状态、朝着什么样的目标继续前进，对团结和激励全国各族人民为夺取中国特色社会主义新胜利而奋斗具有十分重大的意义。广
【K8s】专题十一：Kubernetes 集群证书过期处理方法行者Sun1989 Kubernetes kubernetes 云原生容器
本文内容均来自个人笔记并重新梳理，如有错误欢迎指正！如果对您有帮助，烦请点赞、关注、转发、订阅专栏！专栏订阅入口Linux专栏|Docker专栏|Kubernetes专栏往期精彩文章【Docker】（全网首发）KylinV10下MySQL容器内存占用异常的解决方法【Docker】（全网首发）KylinV10下MySQL容器内存占用异常的解决方法（续）【Docker】MySQL源码构建Docker镜
变频器：原理、应用及其在现代工业与生活中的节能与智能控制作用智能科技前沿人工智能科技生活单片机嵌入式硬件
创作不易，您的打赏、关注、点赞、收藏和转发是我坚持下去的动力！1.变频器的原理变频器（Inverter），是一种将固定频率的交流电（通常是50Hz或60Hz）转换为可变频率和电压的交流电的电气设备。其工作原理是基于电力电子技术和控制理论的应用，能够通过改变供给电机的电源频率来控制电动机的速度和扭矩。变频器的基本工作原理可以分为以下几个阶段：整流：首先，将输入的交流电（AC）通过整流器（通常是二极管
4×4矩阵键盘详解（STM32）辰哥单片机设计 STM32传感器教学矩阵计算机外设 stm32 嵌入式硬件单片机传感器
目录一、介绍二、传感器原理1.原理图2.工作原理介绍三、程序设计main.c文件button4_4.h文件button4_4.c文件四、实验效果五、资料获取项目分享一、介绍矩阵键盘，又称为行列式键盘，是用4条I/O线作为行线，4条I/O线作为列线组成的键盘。在行线和列线的每一个交叉点上设置一个按键，因此键盘中按键的个数是4×4个。这种行列式键盘结构能够有效地提高单片机系统中I/O口的利用率，节约单
社群运营专题第2期——社群促活、留存瓷然
社群的建立不是一日之功，而是日复一日的运营。01以内容引导、拉新留存为主社群建立初期，社群的用户处于100—200人之间，是代购最容易迁入的时期。“垃圾”群初期运营人要进行用户拉新留存和话题内容的引导,日常内容维护包含:与社群有关的小知识、实时热点等。运营人发布内容后无人回复时，可进行小号切换、营造氛围、创造3-5条内容，开启"闲聊"模式，待自带活跃性质的“核心人物”出现。删除一切乱发广告的代购、
学单片机怎么在3-5个月内找到工作？无际单片机编程单片机嵌入式开发物联网 stm32 c语言
每个初学者，都如履薄冰，10几年前，我自学单片机时，也一样。想通过学习，找一份体面点的工作，又害怕辛辛苦苦学出来，找不到工作。好在，当初执行力，还算可以，自学java没成功，后面自学单片机，成功入行了。转眼间，毕业到现在有13年了，马上也到了奔4的年纪。这13年一直在跟单片机打交道，打过工，创过业，对行业，对企业，都有一定的认知，坚持看完这篇内容，相信能帮你少走几个月弯路。有些老铁，加了我很久，时
android进阶之光！Android面试必备的集合源码详解，系列篇程序员Sunbu 程序员 Android
前言面试：如果不准备充分的面试，完全是浪费时间，更是对自己的不负责。文末会给大家分享下我整理的Android面试专题及答案其中大部分都是大企业面试常问的面试题，可以对照这查漏补缺，当然了，这里所列的肯定不可能覆盖全部方式，不过对大家找工作肯定是有帮助！本月飞机到达上海，到今天第6天了，四家大公司华为，小米，映客，抖音，还有二家中小型公司。有几家已经面了几轮，下周还要面，挂了几家，不过目前已经选择了
51单片机：P3.3口输入/P 1口输出实验 li星野单片机
51单片机：P3.3口输入/P1口输出实验一、实验内容1P3.3口做输入口，外接一脉冲,每输入一个脉冲,P1口按十六进制除2（乘2）。2.P1口做输出口，P1口接的8个发光二极管L1—L8按十六进制除2（乘2）方式点亮。二、仿真图三、代码实现C语言实现：#include#includesbitKEY=P3^3;voiddelay10ms(void);voidmain(){charnum=0xfe;
2020-11-12 写单片机内存的脚本 nc openocd 事务自动测试 linuxScripter
这是写单片机内存的脚本：z@z-ThinkPad-T400:~/zworkT400/EDA_heiche/zREPOgit/simple-gcc-stm32-project$catz.wholeRun.oneCase.cmdcattmp6.toWrite|awk'{system("echomwb"$1""$2"|nclocalhost4444");}'catUSER/DEBUG/debug.h|g
单片机中断 woainizhongguo. STM32单片机原理解析篇单片机嵌入式硬件
**在51单片机中，中断向量表的地址是如何被设置的？**在51单片机中，中断向量表的设置是中断系统的核心部分，它定义了中断服务程序的入口地址。以下是中断向量表的设置方法：中断向量表的位置：51单片机的中断向量表通常位于程序存储器的起始位置，即地址0x0000到0x000F（对于双字节的中断向量，实际占用0x0000到0x001F）。这些地址是固定的，由单片机的硬件设计决定。中断向量的分配：每个中断
基于STC12C5A60S2单片机的LED汉字显示系统的设计 lantiandianzi 单片机嵌入式硬件
本设计基于单片机的LED汉字显示装置，该设计以STC12C5A60S2单片机为核心，利用最小系统和多个模块完成设计，包括点阵驱动模块、时钟模块、串口通信模块、红外线接收模块以及LED点阵屏。其中，点阵驱动模块采用74HC245芯片设计完成，结合DS1302时钟芯片完成LED点阵显示屏的汉字与时间显示，使用按键、串口、红外线遥控可以完成时间的实时更新、自定义汉字显示、改变汉字显示颜色、改变汉字滚动方
51单片机-AT24C02-实验2-秒表实验（可参考上一节） Whappy001 51单片机嵌入式硬件单片机
利用定时器去对按键和数码管进行扫描(Whappy)main.c#include#include"LCD1602.h"#include"AT24C02.h"#include"Delay.h"#include"Timer0.h"#include"Nixie.h"#include"Key.h"unsignedcharKeyNum;unsignedcharMin,Sec,MiniSec;unsignedc
单片机在医疗设备中的应用实例教程 kkchenjj 单片机单片机嵌入式硬件
单片机在医疗设备中的应用实例教程单片机基础单片机概述单片机，全称为单片微型计算机（Single-ChipMicrocomputer），是一种将中央处理器（CPU）、存储器、输入输出接口等主要计算机部件集成在一块芯片上的微型计算机系统。它具有体积小、功耗低、成本低廉、控制功能强大等特点，广泛应用于工业控制、家用电器、汽车电子、医疗设备等多个领域。特点集成度高：单片机将计算机的主要部件集成在一块芯片上
单片机与传感器接口技术应用实例教程 kkchenjj 单片机单片机 nosql 嵌入式硬件
单片机与传感器接口技术应用实例教程单片机基础单片机概述单片机，全称为单片微型计算机（Single-ChipMicrocomputer），是一种将中央处理器（CPU）、存储器、输入输出接口等主要计算机部件集成在一块芯片上的微型计算机系统。它具有体积小、功耗低、成本低廉、控制功能强大等特点，广泛应用于工业控制、家用电器、汽车电子、通信设备、医疗器械等领域。特点集成度高：单片机将计算机的主要部件集成在一
C语言《智能自平衡小车，实现平衡功能的基础上，加入了超声波避障、超声波跟随、蓝牙遥控等功能》+源代码+文档说明 jzpfbpx c语言开发语言
文章目录源代码下载地址项目介绍项目功能项目备注源代码下载地址源代码下载地址点击这里下载源码项目介绍C语言《智能自平衡小车，实现平衡功能的基础上，加入了超声波避障、超声波跟随、蓝牙遥控等功能》+源代码+文档说明项目功能为了实现小车功能，小车硬件主要包括：控制核心板带编码器的直流电机车架12V1900mah锂电池项目备注1、该资源内项目代码都经过测试运行成功，功能ok的情况下才上传的，请放心下载使用！
为什么戴森可以？ 9a1c995d045b
你们买的的贼贵的戴森，他们的老板就叫戴森，现在是英国首富。把吹风机卖遍了全世界。为什么他可以？【强到变态的产品力/创新力】让人震撼的是，戴森研发出的第一款产品，用了十五年，是一款无尘吸尘器。出道是用邮购目录的零售方式，迅速打开当地市场，随即跻身百货商店。90年代末，已经享誉全球。吸气的反面是排气，既然独创的电机这么优秀，为什么不反过来做一个吹风机？很快空气干手机就被研发出来，获得了洛杉矶机场的采购
2019-01-21 张盼老师
专题30《我能速读增记忆》。学习目标：一、了解人的眼睛接受文字的信息的速度远远落后于人脑思维的速度。了解速读能使眼睛跳跃式扫描、思维快速运转，做到眼看脑记，眼脑同步。二、尝试在阅读时减少头脑中潜在的发音现象，扩大视区和识记的范围。学会把阅读的主视区放在每一段文字的开头和结尾部分。三、感受速度对提高记忆效率的作用，以及由此带来的快乐体验和自信心。①热身阶段：“过目不忘”有点难。通过一个过目不忘的游戏
【OpenHarmony嵌入式硬件开发】基于OpenHarmony标准系统的C++公共基础类库案例2：SafeMap 青少年编程作品集嵌入式硬件 c++java sql harmonyos 华为华为云
1、程序简介该程序是基于OpenHarmony的C++公共基础类库的安全关联容器：SafeMap。OpenHarmony提供了一个线程安全的map实现。SafeMap在STLmap基础上封装互斥锁，以确保对map的操作安全。本案例主要完成如下工作：创建1个子线程，负责每秒调用EnsureInsert()插入元素；创建1个子线程，负责每秒调用Insert()插入元素；创建1个子线程，负责每秒调用Er
阀门定位器 ZHD18060503853 单片机嵌入式硬件
阀门定位器：（福克斯波罗,YTC，山武）PLC：（西门子，施耐德，ABB,AB,三菱，欧姆龙）泵阀：（威格士，哈威，伊顿，阿托斯)传感器：（倍加福，西克，伦茨，巴鲁夫，易福门，图尔克，安川)编码器：（海德汉，堡盟，亨士乐）西门子：罗宾康，6AG1模块,6FC5851数控软件，3UF电机保护器，数控卡件，烟气分析仪霍尼韦尔：微动开关，测厚仪配件，麦克森燃烧ABB：DCS，张力控制器，压力计，机器人配
A20B-8002-0020发那科 ZHD18060503853 自动化
阀门定位器：（福克斯波罗,YTC，山武）PLC：（西门子，施耐德，ABB,AB,三菱，欧姆龙）泵阀：（威格士，哈威，伊顿，阿托斯)传感器：（倍加福，西克，伦茨，巴鲁夫，易福门，图尔克，安川)编码器：（海德汉，堡盟，亨士乐）西门子：罗宾康，6AG1模块,6FC5851数控软件，3UF电机保护器，数控卡件，烟气分析仪霍尼韦尔：微动开关，测厚仪配件，麦克森燃烧ABB：DCS，张力控制器，压力计，机器人配
东芝 TB67S128FTG：释放精密电机控制的力量东芝、铠侠总代13610068393 单片机嵌入式硬件
在电机控制领域，精度和效率至关重要。东芝的TB67S128FTG是一款专为先进电机控制应用设计的两相双极步进电机驱动器。让我们深入了解这款出色的芯片的功能和优点。TB67S128FTG概述TB67S128FTG是一款采用东芝BiCD工艺（结合双极、CMOS和DMOS技术）设计的高度集成的单片IC。此集成实现了高性能和可靠性，使TB67S128FTG成为需要精确电机控制的各种应用（如3D打印机、工业
【不一样】５月联合主题征文非村
故事与小说伯乐非村、冬天开的猫【不一样】主题专区，每月指定一句话做为文章开头，由作者接续成文，自由创意。两位伯乐指定句会有些许不同，作者可自由决定要以哪句话作为开头，完成后将作品投稿至【不一样】专题。我们将从投稿中择优推文，并依喜爱度给予收录奖励20~50贝不等，每期活动结束后，伯乐会从当期推文中各自选出“伯乐最爱奖”并给予666贝奖励，若没有最爱的作品，那就没有。本期主题：非村指定句：终于要过去
掌握单片机,其实并不难培林将军单片机嵌入式硬件
Fearwillbeyourenemy恐惧将会是你的敌人单片机的学习绝不仅仅是对一项知识的掌握。想要学好单片机，需要从硬件结构、内部资源、外设应用等几个方面多方位入手。而要想成为一名嵌入式工程师，就要对单片机的基础非常熟悉，并且掌握C语言当中各个功能的初始化、启动、停止各类函数的编写调试。那么想要掌握单片机需要从哪几个方面入手呢？数字I/O的应用在大多数的单片机实验中，跑马灯实验正是数字I/O的典
ASM系列六利用TreeApi 添加和移除类成员 lijingyao8206 jvm 动态代理 ASM 字节码技术 TreeAPI
同生成的做法一样，添加和移除类成员只要去修改fields和methods中的元素即可。这里我们拿一个简单的类做例子，下面这个Task类，我们来移除isNeedRemove方法，并且添加一个int 类型的addedField属性。 package asm.core; /** * Created by yunshen.ljy on 2015/6/
Springmvc-权限设计 bee1314 spring Web jsp
万丈高楼平地起。权限管理对于管理系统而言已经是标配中的标配了吧，对于我等俗人更是不能免俗。同时就目前的项目状况而言，我们还不需要那么高大上的开源的解决方案，如Spring Security，Shiro。小伙伴一致决定我们还是从基本的功能迭代起来吧。目标： 1.实现权限的管理（CRUD） 2.实现部门管理（CRUD) 3.实现人员的管理（CRUD） 4.实现部门和权限
算法竞赛入门经典（第二版）第2章习题 CrazyMizzz c 算法
2.4.1 输出技巧 #include <stdio.h> int main() { int i, n; scanf("%d", &n); for (i = 1; i <= n; i++) printf("%d\n", i); return 0; } 习题2-2 水仙花数(daffodil
struts2中jsp自动跳转到Action 麦田的设计者 jsp webxml struts2 自动跳转
1、在struts2的开发中，经常需要用户点击网页后就直接跳转到一个Action，执行Action里面的方法，利用mvc分层思想执行相应操作在界面上得到动态数据。毕竟用户不可能在地址栏里输入一个Action（不是专业人士） 2、＜jsp:forward page="xxx.action" /＞，这个标签可以实现跳转，page的路径是相对地址,不同与jsp和j
php 操作webservice实例 IT独行者 PHP webservice
首先大家要简单了解了何谓webservice，接下来就做两个非常简单的例子，webservice还是逃不开server端与client端。我测试的环境为：apache2.2.11 php5.2.10做这个测试之前，要确认你的php配置文件中已经将soap扩展打开，即extension=php_soap.dll; OK 现在我们来体验webservice //server端 serve
Windows下使用Vagrant安装linux系统 _wy_ windows vagrant
准备工作：下载安装 VirtualBox ：https://www.virtualbox.org/ 下载安装 Vagrant ：http://www.vagrantup.com/ 下载需要使用的 box ：官方提供的范例：http://files.vagrantup.com/precise32.box 还可以在 http://www.vagrantbox.es/
更改linux的文件拥有者及用户组(chown和chgrp) 无量 c linux chgrp chown
本文（转） http://blog.163.com/yanenshun@126/blog/static/128388169201203011157308/ http://ydlmlh.iteye.com/blog/1435157 一、基本使用：使用chown命令可以修改文件或目录所属的用户：命令
linux下抓包工具矮蛋蛋 linux
原文地址： http://blog.chinaunix.net/uid-23670869-id-2610683.html tcpdump -nn -vv -X udp port 8888 上面命令是抓取udp包、端口为8888 netstat -tln 命令是用来查看linux的端口使用情况 13 . 列出所有的网络连接 lsof -i 14. 列出所有tcp 网络连接信息 l
我觉得mybatis是垃圾！：“每一个用mybatis的男纸，你伤不起” alafqq mybatis
最近看了每一个用mybatis的男纸，你伤不起原文地址：http://www.iteye.com/topic/1073938 发表一下个人看法。欢迎大神拍砖；个人一直使用的是Ibatis框架，公司对其进行过小小的改良；最近换了公司，要使用新的框架。听说mybatis不错；就对其进行了部分的研究；发现多了一个mapper层；个人感觉就是个dao；
解决java数据交换之谜百合不是茶数据交换
交换两个数字的方法有以下三种，其中第一种最常用 /* 输出最小的一个数 */ public class jiaohuan1 { public static void main(String[] args) { int a =4; int b = 3; if(a<b){ // 第一种交换方式 int tmep =
渐变显示 bijian1013 JavaScript
<style type="text/css"> #wxf { FILTER: progid:DXImageTransform.Microsoft.Gradient(GradientType=0, StartColorStr=#ffffff, EndColorStr=#97FF98); height: 25px; } </style>
探索JUnit4扩展：断言语法assertThat bijian1013 java 单元测试 assertThat
一.概述 JUnit 设计的目的就是有效地抓住编程人员写代码的意图，然后快速检查他们的代码是否与他们的意图相匹配。 JUnit 发展至今，版本不停的翻新，但是所有版本都一致致力于解决一个问题，那就是如何发现编程人员的代码意图，并且如何使得编程人员更加容易地表达他们的代码意图。JUnit 4.4 也是为了如何能够
【Gson三】Gson解析{"data":{"IM":["MSN","QQ","Gtalk"]}} bit1129 gson
如何把如下简单的JSON字符串反序列化为Java的POJO对象? {"data":{"IM":["MSN","QQ","Gtalk"]}} 下面的POJO类Model无法完成正确的解析： import com.google.gson.Gson;
【Kafka九】Kafka High Level API vs. Low Level API bit1129 kafka
1. Kafka提供了两种Consumer API High Level Consumer API Low Level Consumer API(Kafka诡异的称之为Simple Consumer API，实际上非常复杂) 在选用哪种Consumer API时，首先要弄清楚这两种API的工作原理，能做什么不能做什么，能做的话怎么做的以及用的时候，有哪些可能的问题
在nginx中集成lua脚本：添加自定义Http头，封IP等 ronin47 nginx lua
Lua是一个可以嵌入到Nginx配置文件中的动态脚本语言，从而可以在Nginx请求处理的任何阶段执行各种Lua代码。刚开始我们只是用Lua 把请求路由到后端服务器，但是它对我们架构的作用超出了我们的预期。下面就讲讲我们所做的工作。强制搜索引擎只索引mixlr.com Google把子域名当作完全独立的网站，我们不希望爬虫抓取子域名的页面，降低我们的Page rank。 location /{
java-归并排序 bylijinnan java
import java.util.Arrays; public class MergeSort { public static void main(String[] args) { int[] a={20,1,3,8,5,9,4,25}; mergeSort(a,0,a.length-1); System.out.println(Arrays.to
Netty源码学习-CompositeChannelBuffer bylijinnan java netty
CompositeChannelBuffer体现了Netty的“Transparent Zero Copy” 查看API（ http://docs.jboss.org/netty/3.2/api/org/jboss/netty/buffer/package-summary.html#package_description）可以看到，所谓“Transparent Zero Copy”是通
Android中给Activity添加返回键 hotsunshine Activity
// this need android:minSdkVersion="11" getActionBar().setDisplayHomeAsUpEnabled(true); @Override public boolean onOptionsItemSelected(MenuItem item) {
静态页面传参 ctrain 静态
$(document).ready(function () { var request = { QueryString : function (val) { var uri = window.location.search; var re = new RegExp("" + val + "=([^&?]*)", &
Windows中查找某个目录下的所有文件中包含某个字符串的命令 daizj windows 查找某个目录下的所有文件包含某个字符串
findstr可以完成这个工作。 [html] view plain copy >findstr /s /i "string" *.* 上面的命令表示，当前目录以及当前目录的所有子目录下的所有文件中查找"string&qu
改善程序代码质量的一些技巧 dcj3sjt126com 编程 PHP 重构
有很多理由都能说明为什么我们应该写出清晰、可读性好的程序。最重要的一点，程序你只写一次，但以后会无数次的阅读。当你第二天回头来看你的代码时，你就要开始阅读它了。当你把代码拿给其他人看时，他必须阅读你的代码。因此，在编写时多花一点时间，你会在阅读它时节省大量的时间。让我们看一些基本的编程技巧：尽量保持方法简短尽管很多人都遵
SharedPreferences对数据的存储 dcj3sjt126com
SharedPreferences简介： &nbs
linux复习笔记之bash shell (2) bash基础 eksliang bash bash shell
转载请出自出处： http://eksliang.iteye.com/blog/2104329 1.影响显示结果的语系变量（locale） 1.1locale这个命令就是查看当前系统支持多少种语系，命令使用如下： [root@localhost shell]# locale LANG=en_US.UTF-8 LC_CTYPE="en_US.UTF-8"
Android零碎知识总结 gqdy365 android
1、CopyOnWriteArrayList add(E) 和remove(int index)都是对新的数组进行修改和新增。所以在多线程操作时不会出现java.util.ConcurrentModificationException错误。所以最后得出结论：CopyOnWriteArrayList适合使用在读操作远远大于写操作的场景里，比如缓存。发生修改时候做copy，新老版本分离，保证读的高
HoverTree.Model.ArticleSelect类的作用 hvt Web .net C#hovertree asp.net
ArticleSelect类在命名空间HoverTree.Model中可以认为是文章查询条件类，用于存放查询文章时的条件，例如HvtId就是文章的id。HvtIsShow就是文章的显示属性，当为-1是，该条件不产生作用，当为0时，查询不公开显示的文章，当为1时查询公开显示的文章。HvtIsHome则为是否在首页显示。HoverTree系统源码完全开放，开发环境为Visual Studio 2013
PHP 判断是否使用代理 PHP Proxy Detector 天梯梦 proxy
1. php 类 I found this class looking for something else actually but I remembered I needed some while ago something similar and I never found one. I'm sure it will help a lot of developers who try to
apache的math库中的回归——regression（翻译） lvdccyb Math apache
这个Math库，虽然不向weka那样专业的ML库，但是用户友好，易用。多元线性回归，协方差和相关性（皮尔逊和斯皮尔曼），分布测试（假设检验，t，卡方，G），统计。数学库中还包含，Cholesky，LU，SVD，QR，特征根分解，真不错。基本覆盖了：线代，统计，矩阵，最优化理论曲线拟合常微分方程遗传算法（GA），还有3维的运算。。。
基础数据结构和算法十三：Undirected Graphs (2) sunwinner Algorithm
Design pattern for graph processing. Since we consider a large number of graph-processing algorithms, our initial design goal is to decouple our implementations from the graph representation
云计算平台最重要的五项技术 sumapp 云计算云平台智城云
云计算平台最重要的五项技术 1、云服务器云服务器提供简单高效，处理能力可弹性伸缩的计算服务，支持国内领先的云计算技术和大规模分布存储技术，使您的系统更稳定、数据更安全、传输更快速、部署更灵活。特性机型丰富通过高性能服务器虚拟化为云服务器，提供丰富配置类型虚拟机，极大简化数据存储、数据库搭建、web服务器搭建等工作；仅需要几分钟，根据CP
《京东技术解密》有奖试读获奖名单公布 ITeye管理员活动
ITeye携手博文视点举办的12月技术图书有奖试读活动已圆满结束，非常感谢广大用户对本次活动的关注与参与。 12月试读活动回顾： http://webmaster.iteye.com/blog/2164754 本次技术图书试读活动获奖名单及相应作品如下：一等奖（两名） Microhardest：http://microhardest.ite

按字母分类： A B C D E F G H I J K L M N O P Q R S T U V W X Y Z 其他