哈夫曼树的基本概念及其构建（C++）

哈夫曼树的基本概念：

 

在了解哈夫曼树的概念之前，我们要了解到的是带权路径长度的概念：

1. 在实际应用当中，树中的结点往往都会被赋予某种意义的数值，这个数值就称为该结点的权；
2. 从根结点到任意结点的路径长度（经过的边数）与该结点上的权值得乘积称之为该结点的带权路径长度；
3. 树中所有叶结点的带权路径长度称为该树的带权路径长度（WPL），其计算公式如下：

 那么可以想象，给定n（n>1）个结点，并给定每个结点的权值，构造出来的树是有许多中的，每种树的WPL也可能不同，那么在这些构造出来的树当中，WPL最小的那颗树就称之为哈夫曼树，也称之为最优二叉树。

 

哈夫曼树的应用：

由哈夫曼树的特性，衍生出来的应用场景是非常多的，其中应用最多的就是压缩编码。

哈夫曼树的构造：

哈夫曼树的构造的基本思想其实就是，在给定的n个结点序列中，每次选取两个权值最小的两个结点凑成一颗二叉树，这两个结点的权值之和就是它们的新根结点，将这个新的新结点从新放回序列中，循环上述操作，直至最终所有的结点序列构建成一颗二叉树，也就是最终的哈夫曼树。

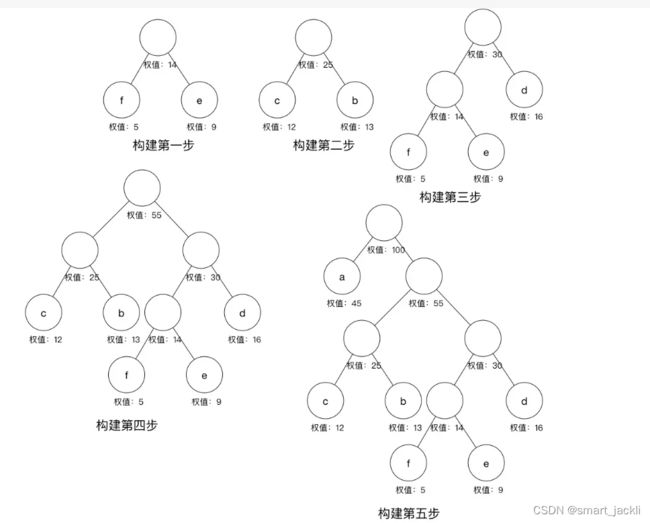
以序列{a(45),b(13),c(12),d(16),e(9),f(5)}为例，建立哈夫曼树的步骤如下所示：

哈夫曼树构造过程：

运用不同的存储方式和结点定义方式，代码有些许不同，但是整体的编码思想就是上述过程的衍生，本文以最简单的顺序存储来实现哈夫曼树的构造：

1.结点定义：

由哈夫曼树的性质其实可以推出哈夫曼树结点所具备的基本要素：

 包括了元素，父节点，左孩子结点，右孩子结点，权值。

那么定义如下：

typedef struct {
	char data; //元素
	int weight; //权值
	int parent, lch,rch; //父节点，左孩子，右孩子
}HTNode,*HuffmanTree;

2.构造哈夫曼树：

void CreateHuffmanTree(HuffmanTree& HT, int n)
{
	if (n <= 1)  cout << "error" << endl;
	int s1, s2;
	int m = n * 2 - 1;  // 没有度为1的节点，则总结点是2*叶子节点数-1个 
	HT = new HTNode[m + 1];
	for (int i = 1; i <= m; ++i)  // 初始化 
	{
		HT[i].data = '*';  //所有结点元素值设为‘*’，根据自己的需要可以更改或者删除这行代码
		HT[i].parent = 0; 
		HT[i].lch = 0;
		HT[i].rch = 0;
	}
	for (int i = 1; i <= n; ++i)
	{
		cin >> HT[i].data >> HT[i].weight; //从键盘输入结点元素值和权值
	}
	for (int i = n + 1; i <= m; ++i)
	{
		select(HT, i - 1, s1, s2);  // 从前面的范围里选择权重最小的两个节点 
		HT[s1].parent = i;  
		HT[s2].parent = i;
		HT[i].lch = s1;
		HT[i].rch = s2;
		HT[i].weight = HT[s1].weight + HT[s2].weight;  // 得到一个新节点 
	}
}

3.选择最小两个结点：

void select(HuffmanTree HT, int top, int  &s1, int &s2)
{
	int min = INT_MAX;
	for (int i = 1; i <= top; ++i)  // 选择没有双亲的节点中，权重最小的节点 
	{
		if (HT[i].weight < min && HT[i].parent == 0)
		{
			min = HT[i].weight;
			s1 = i;
		}
	}
	min = INT_MAX;
	for (int i = 1; i <= top; ++i)  // 选择没有双亲的节点中，权重次小的节点 
	{
		if (HT[i].weight < min && i != s1 && HT[i].parent == 0)
		{
			min = HT[i].weight;
			s2 = i;
		}
	}
}

完整代码：

#include
using namespace std;
typedef struct {
	char data;
	int weight;
	int parent, lch,rch;
}HTNode,*HuffmanTree;
void select(HuffmanTree HT, int top, int  &s1, int &s2)
{
	int min = INT_MAX;
	for (int i = 1; i <= top; ++i)  // 选择没有双亲的节点中，权重最小的节点 
	{
		if (HT[i].weight < min && HT[i].parent == 0)
		{
			min = HT[i].weight;
			s1 = i;
		}
	}
	min = INT_MAX;
	for (int i = 1; i <= top; ++i)  // 选择没有双亲的节点中，权重次小的节点 
	{
		if (HT[i].weight < min && i != s1 && HT[i].parent == 0)
		{
			min = HT[i].weight;
			s2 = i;
		}
	}
}

void CreateHuffmanTree(HuffmanTree& HT, int n)
{
	if (n <= 1)  cout << "error" << endl;
	int s1, s2;
	int m = n * 2 - 1;  // 没有度为1的节点，则总结点是2*叶子节点数-1个 
	HT = new HTNode[m + 1];
	for (int i = 1; i <= m; ++i)  // 初始化 
	{
		HT[i].data = '*';
		HT[i].parent = 0;
		HT[i].lch = 0;
		HT[i].rch = 0;
	}
	for (int i = 1; i <= n; ++i)
	{
		cin >> HT[i].data >> HT[i].weight;
	}
	for (int i = n + 1; i <= m; ++i)
	{
		select(HT, i - 1, s1, s2);  // 从前面的范围里选择权重最小的两个节点 
		HT[s1].parent = i;
		HT[s2].parent = i;
		HT[i].lch = s1;
		HT[i].rch = s2;
		HT[i].weight = HT[s1].weight + HT[s2].weight;  // 得到一个新节点 
	}
}
int main() {
	HuffmanTree hf;
	CreateHuffmanTree(hf, 5);
	for (int i = 1; i <= 9; i++)
	{
		cout<< i <<": " << hf[i].data << " " << hf[i].weight << " "<

执行结果：