8、VAE:变分自编码器
目录
一、背景与动机
二、创新与卖点
三、实现细节
VAE模型架构
损失函数
VAE的背后的数学原理
简易代码
四、总结
一、背景与动机
在深度学习领域,数据的有效表示和生成模型一直是研究的重点。VAE,即变分自编码器(Variational Auto-Encoder),正是在这种背景下应运而生的前沿技术。它结合了自编码器和概率图模型的优点,旨在解决高维复杂数据的高效表示和生成问题。
VAE最想解决的问题是什么?
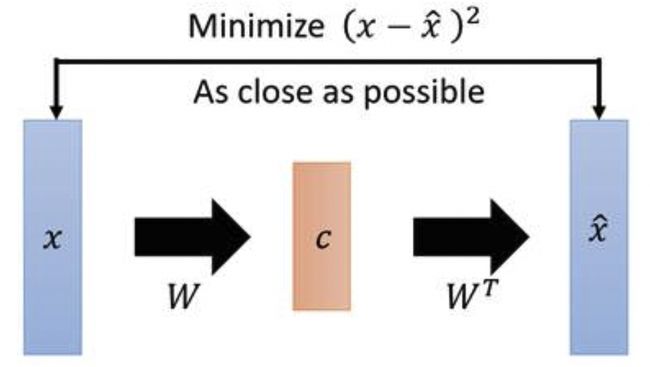
首先是如何构造编码器和解码器,使得图片能够编码成易于表示的形态,并且这一形态能够尽可能无损地解码回原真实图像。这与PCA(主成分分析)有些相似,而PCA本身是用来做矩阵降维的:
![]() 本身是一个矩阵,通过一个变换
本身是一个矩阵,通过一个变换![]() 变成了一个低维矩阵
变成了一个低维矩阵![]() ,因为这一过程是线性的,所以再通过一个
,因为这一过程是线性的,所以再通过一个![]() 变换就能还原出一个
变换就能还原出一个![]() ,现在我们要找到一种变换
,现在我们要找到一种变换![]() ,使得矩阵
,使得矩阵![]() 与
与![]() 能够尽可能地一致,这就是PCA做的事情。在PCA中找这个变换
能够尽可能地一致,这就是PCA做的事情。在PCA中找这个变换![]() 用到的方法是SVD(奇异值分解)算法,这是一个纯数学方法。
用到的方法是SVD(奇异值分解)算法,这是一个纯数学方法。
PCA与我们想要构造的自编码器的相似之处是在于,如果把矩阵![]() 视作输入图像,
视作输入图像,![]() 视作一个编码器,低维矩阵
视作一个编码器,低维矩阵![]() 视作图像的编码,然后
视作图像的编码,然后![]() 和
和![]() 分别视作解码器和生成图像,PCA就变成了一个自编码器网络模型的雏形。
分别视作解码器和生成图像,PCA就变成了一个自编码器网络模型的雏形。
所以首先最明显能改进的地方是用神经网络代替变换![]() 和
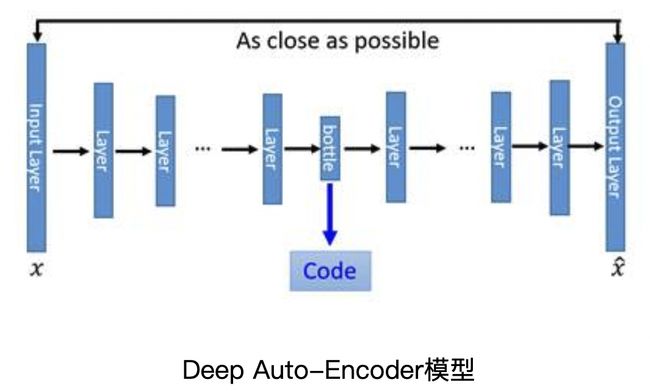
和![]() 变换,就得到了如下Deep Auto-Encoder模型:
变换,就得到了如下Deep Auto-Encoder模型:
这一替换的明显好处是,引入了神经网络强大的拟合能力,使得编码(Code)的维度能够比原始图像![]() 的维度低非常多。但是这并没有达到我们真正想要构造的生成模型的标准。
的维度低非常多。但是这并没有达到我们真正想要构造的生成模型的标准。
对于一个生成模型而言,解码器部分应该是单独能够提取出来的,并且对于在规定维度下任意采样的一个编码,都应该能通过解码器产生一张清晰且真实的图片。
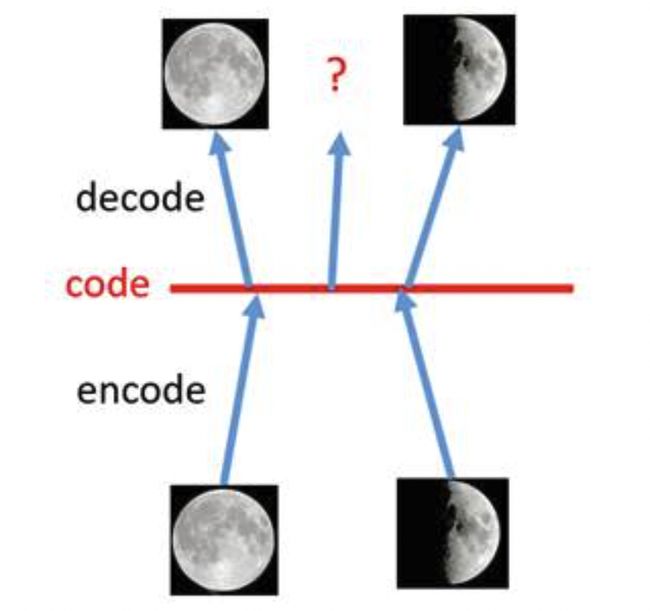
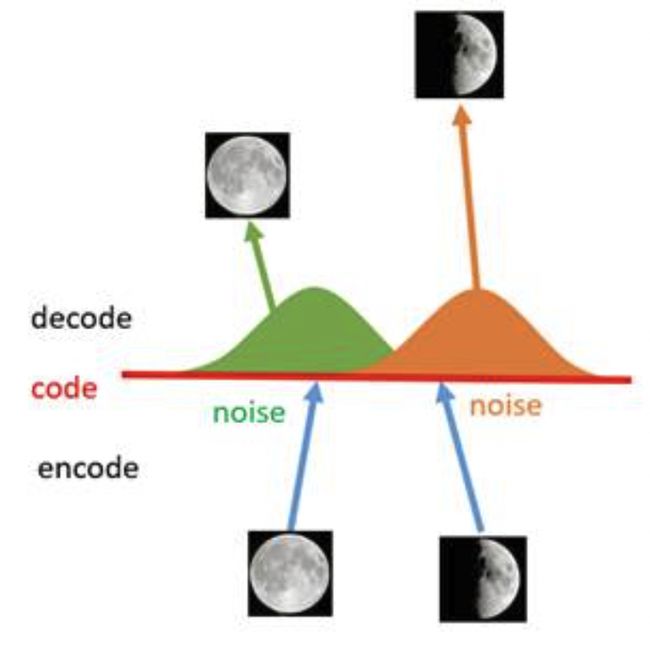
假设有两张训练图片,一张是全月图,一张是半月图,经过训练的自编码器模型能无损地还原这两张图片。如果在code空间上,两张图片的编码点中间处取一点,然后将这一点交给解码器,我们希望新的生成图片是一张清晰的图片(类似3/4全月的样子)。但是,实际的结果是,生成图片是模糊且无法辨认的乱码图。其原因是因为:1、编码和解码的过程使用了深度神经网络,这是一个非线性的变换过程,所以在code空间上点与点之间的迁移是非常没有规律的。2、神经网络强大的拟合能力造成了过拟合现象。使得生成模型生成图像的过程渐渐变成查字典的现象。
如何解决这个问题呢?我们可以引入噪声,使得图片的编码区域得到扩大,从而掩盖掉失真的空白编码点。
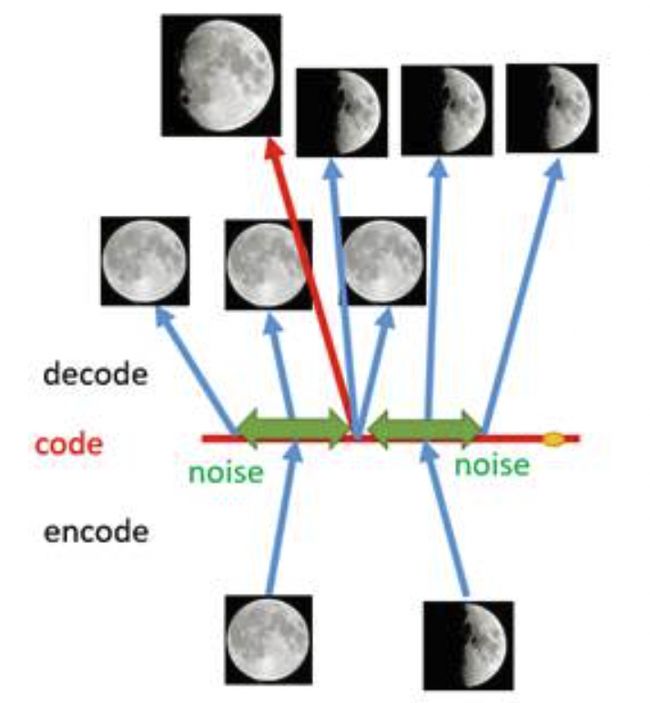
现在在给两张图片编码的时候加上一点噪音,使得每张图片的编码点出现在绿色箭头所示范围内,于是在训练模型的时候,绿色箭头范围内的点都有可能被采样到,这样解码器在训练时会把绿色范围内的点都尽可能还原成和原图相似的图片。然后我们可以关注之前那个失真点,现在它处于全月图和半月图编码的交界上,于是解码器希望它既要尽量相似于全月图,又要尽量相似于半月图,于是它的还原结果就是两种图的折中(3/4全月图)。
给编码器增添一些噪音,可以有效覆盖失真区域。不过这还并不充分,因为在上图的距离训练区域很远的黄色点处,它依然不会被覆盖到,仍是个失真点。为了解决这个问题,我们可以试图把噪音无限拉长,使得对于每一个样本,它的编码会覆盖整个编码空间,不过我们得保证,在原编码附近编码的概率最高,离原编码点越远,编码概率越低。在这种情况下,图像的编码就由原先离散的编码点变成了一条连续的编码分布曲线,如下图所示。
这种将图像编码由离散变为连续的方法,就是变分自编码的核心思想。
二、创新与卖点
-
隐变量建模:VAE的核心创新在于对隐变量的处理上。在VAE中,每个输入样本对应一个隐藏的随机变量,这个随机变量遵循一定的概率分布,通过最大化观测数据下隐藏变量的后验概率,使得学习到的隐含空间既能保留数据的主要特征,又能捕捉数据的概率结构。
-
变分推断:VAE利用变分推断方法近似难以直接计算的后验概率分布,通过优化一个可计算的变分下界(Evidence Lower Bound, ELBO)来间接地最大化模型的似然性。这一策略为复杂概率模型的学习提供了一种可行且高效的解决方案。
-
生成能力:VAE强大的卖点在于其生成能力。由于其能学习到数据的概率分布,因此可以用来生成全新的、未在训练集中出现过的数据样本,这在图像生成、文本生成等领域具有广泛的应用前景。
三、实现细节
VAE模型架构
AE的架构:
AutoEncoder通过encode和decode实现,与PCA类似,在卷积的AutoEncoder中,encode通过卷积池化进行降维,decode通过反卷积进行升维,目标是使输入和输出图片的差异性最小。
VAE的架构:
需要注意的是,图中的![]() 和正太分布
和正太分布![]() 中不是一回事。实际上模型输出的是
中不是一回事。实际上模型输出的是![]() (正太分布标准差的log值)。
(正太分布标准差的log值)。
在auto-encoder中,编码器是直接产生一个编码的,但是在VAE中,为了给编码添加合适的噪音,编码器会输出两个编码,一个是原有编码![]() ,另外一个是控制噪音干扰程度的编码
,另外一个是控制噪音干扰程度的编码![]() ,第二个编码其实很好理解,就是为随机噪音码
,第二个编码其实很好理解,就是为随机噪音码![]() 分配权重,然后加上exp(
分配权重,然后加上exp(![]() )的目的是为了保证这个分配的权重是个正值,最后将原编码与噪音编码相加,就得到了VAE在code层的输出结果
)的目的是为了保证这个分配的权重是个正值,最后将原编码与噪音编码相加,就得到了VAE在code层的输出结果![]() 。其它网络架构都与Deep Auto-encoder无异。
。其它网络架构都与Deep Auto-encoder无异。
为什么是这样子实现的呢?
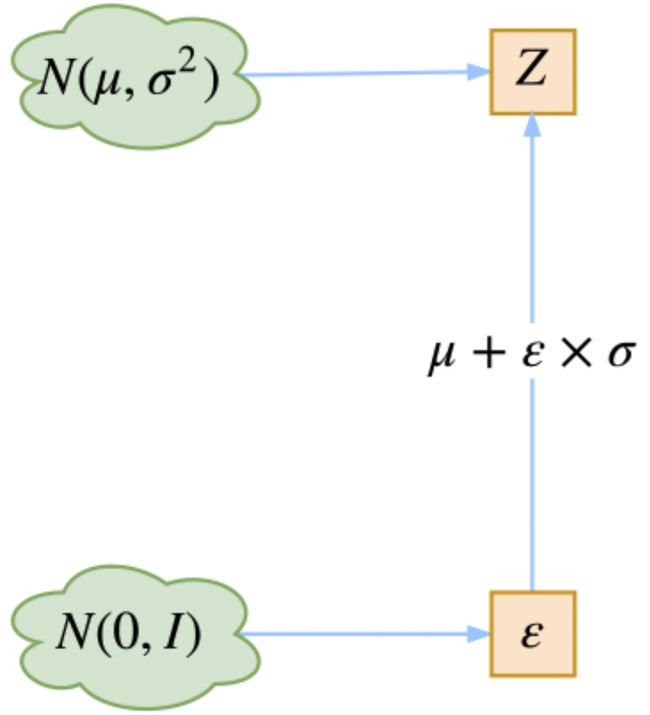
是实现模型的一个技巧,英文名是reparameterization trick,重参数。其实很简单,就是我们要从![]() 中采样一个
中采样一个![]() (这里的
(这里的![]() 其实就是上面的
其实就是上面的![]() )出来。尽管我们知道了
)出来。尽管我们知道了![]() 中是正态分布,但是均值方差都是靠模型算出来的,我们要靠这个过程反过来优化均值方差的模型,但是“采样”这个操作是不可导的,而采样的结果是可导的。所以我们迂回一下,想得到从
中是正态分布,但是均值方差都是靠模型算出来的,我们要靠这个过程反过来优化均值方差的模型,但是“采样”这个操作是不可导的,而采样的结果是可导的。所以我们迂回一下,想得到从![]() 中采样一个
中采样一个![]() ,相当于从
,相当于从![]() 中采样一个
中采样一个![]() ,然后让
,然后让![]() 。
。
所以其实整体框架这样更好理解一点:
损失函数
损失函数也是一个很关键的点,除了必要的重构损失外,VAE还增添了一个损失函数。首先,我们希望重构![]() ,也就是最小化输入与输出的误差,但是这个重构过程受到噪声的影响,因为
,也就是最小化输入与输出的误差,但是这个重构过程受到噪声的影响,因为![]() 是通过重新采样过的,不是直接由encoder算出来的。显然噪声会增加重构的难度,不过好在这个噪声强度(也就是方差)通过一个神经网络算出来的,所以最终模型为了重构得更好,肯定会想尽办法让方差为0。而方差为0的话,也就没有随机性了,所以不管怎么采样其实都只是得到确定的结果(也就是均值),只拟合一个当然比拟合多个要容易,而均值是通过另外一个神经网络算出来的。说白了,模型会慢慢退化成普通的AutoEncoder,噪声不再起作用。
是通过重新采样过的,不是直接由encoder算出来的。显然噪声会增加重构的难度,不过好在这个噪声强度(也就是方差)通过一个神经网络算出来的,所以最终模型为了重构得更好,肯定会想尽办法让方差为0。而方差为0的话,也就没有随机性了,所以不管怎么采样其实都只是得到确定的结果(也就是均值),只拟合一个当然比拟合多个要容易,而均值是通过另外一个神经网络算出来的。说白了,模型会慢慢退化成普通的AutoEncoder,噪声不再起作用。
所以VAE还让所有的![]() 都向标准正态分布看齐,这样就防止了噪声为零,同时保证了模型具有生成能力。具体的做法是计算一般(各分量独立的)正态分布与标准正态分布的KL散度。
都向标准正态分布看齐,这样就防止了噪声为零,同时保证了模型具有生成能力。具体的做法是计算一般(各分量独立的)正态分布与标准正态分布的KL散度。
VAE的背后的数学原理
VAE的理论基础是高斯混合模型。
首先我们有一批数据样本![]() ,其整体用X来描述,我们本想根据
,其整体用X来描述,我们本想根据![]() 得到
得到![]() 的分布
的分布![]() ,如果能得到的话,那我直接根据
,如果能得到的话,那我直接根据![]() 来采样,就可以得到所有可能的
来采样,就可以得到所有可能的![]() 了(包括
了(包括![]() 以外的),这是一个终极理想的生成模型了。当然,直接通过样本来求
以外的),这是一个终极理想的生成模型了。当然,直接通过样本来求![]() 是很难实现的。所以要另辟蹊径。
是很难实现的。所以要另辟蹊径。
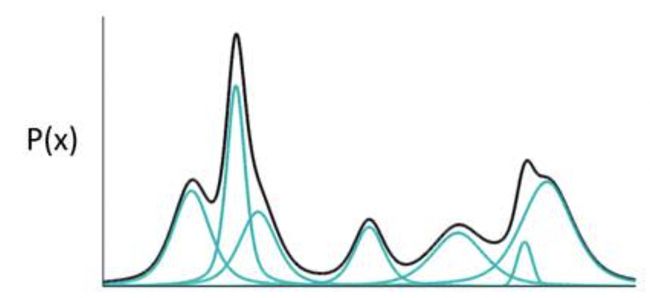
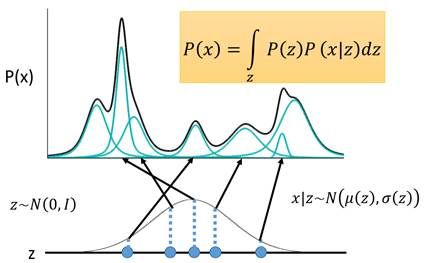
如果![]() 代表一种分布的话,存在一种拆分方法能让它表示成图中若干浅蓝色曲线对应的高斯分布的叠加。只要拆分的数量足够多,其叠加的分布相对于原始分布而言,误差就会非常非常小。
代表一种分布的话,存在一种拆分方法能让它表示成图中若干浅蓝色曲线对应的高斯分布的叠加。只要拆分的数量足够多,其叠加的分布相对于原始分布而言,误差就会非常非常小。
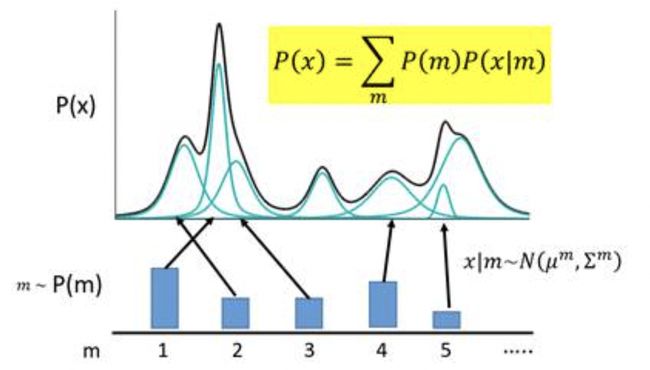
于是我们可以利用这一理论模型去描述这个复杂的![]() 。一种最直接的思路是,直接用每一组高斯分布的参数作为一个编码值实现编码。
。一种最直接的思路是,直接用每一组高斯分布的参数作为一个编码值实现编码。
图中,![]() 代表着每一个高斯组件的编码,
代表着每一个高斯组件的编码,![]() 会服从于一个概率分布
会服从于一个概率分布![]() (多项式分布)。现在编码的对应关系是,每采样一个
(多项式分布)。现在编码的对应关系是,每采样一个![]() ,其对应到一个小的高斯分布
,其对应到一个小的高斯分布![]() ,
,![]() 就可以等价为所有的这些高斯分布的叠加,即:
就可以等价为所有的这些高斯分布的叠加,即:
其中,![]() ,
,![]() 。
。
有了这个模型之后,将来我们需要产生一个样本怎么产生呢? 首先,首先我们根据![]() 的概率采样一个
的概率采样一个![]() , 再根据
, 再根据![]() 找到对应的高斯分布,得到其均值方差,就可以根据这个高斯分布产生一个样本。
找到对应的高斯分布,得到其均值方差,就可以根据这个高斯分布产生一个样本。
上述的这种编码方式是非常简单粗暴的,它对应的是我们之前提到的离散的、有大量失真区域的编码方式。
VAE将这种离散的编码换成一个连续变量z,规定z服从正态分布![]() ,(实际上并不一定要选用
,(实际上并不一定要选用![]() ,其他的连续分布都是可行的)。将每对于一个采样
,其他的连续分布都是可行的)。将每对于一个采样![]() ,会有两个函数
,会有两个函数![]() 和
和![]() ,分别决定z对应到的高斯分布的均值和方差,然后在积分域上所有的高斯分布的累加就成为了原始分布P(X),即用无限个高斯去逼近真实分布:
,分别决定z对应到的高斯分布的均值和方差,然后在积分域上所有的高斯分布的累加就成为了原始分布P(X),即用无限个高斯去逼近真实分布:
![]()
其中,![]() ,
,![]() 。
。
接下来就可以求解这个式子。由于![]() 是已知的,
是已知的,![]() 未知,而
未知,而![]()
,于是我们真正需要求解的,是![]() 和
和![]() 两个函数的表达式。根据极大似然估计,对于给定的x,我们希望所有的样本发生的可能性越大越好,这等价于求解:
两个函数的表达式。根据极大似然估计,对于给定的x,我们希望所有的样本发生的可能性越大越好,这等价于求解:
![]()
又因为![]() 通常非常复杂,导致
通常非常复杂,导致 ![]() 和
和![]() 难以计算,我们需要引入两个神经网络来帮助我们求解。
难以计算,我们需要引入两个神经网络来帮助我们求解。
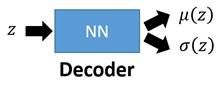
第一个神经网络叫做Decoder,它求解的是 ![]() 和
和![]() 两个函数,这等价于求解
两个函数,这等价于求解![]() 。
。
但问题是这个z怎么来呢,我们不能穷举z的所有空间来做这件事情,我们虽然规定z是属于标准正态分布,但其实在这个z空间中很多地方没法生成我们的图像分布。我们没法把所有的z都穷举完了去算那个表达式。我们现在有的是一批训练样本![]() , 所以我们可以考虑用现有样本去生成那些可以产生图像分布的
, 所以我们可以考虑用现有样本去生成那些可以产生图像分布的![]() , (其目的就是要确定z空间中哪些z是有效的,辅助第一个Decoder求解
, (其目的就是要确定z空间中哪些z是有效的,辅助第一个Decoder求解![]()
)所以要引入第二个神经网络叫做Encoder,它求解的结果是![]() ,给定样本,生成对应的
,给定样本,生成对应的![]() 。
。
绝大数情况下,我们所拥有的数据是非常有限的,导致![]() 的真实分布总是未知的,因此我们希望基于已有的数据,通过一个神经网络即编码器来近似该分布
的真实分布总是未知的,因此我们希望基于已有的数据,通过一个神经网络即编码器来近似该分布
注意到:
上式的第二项是一个大于等于0的值,于是我们就找到了一个![]() 的下界:
的下界:
我们把这个下界记作
 。
。
而求解maximum![]() 就转化为了求解maximum
就转化为了求解maximum ![]() 。
。
注意到:
我们先来求第一项,展开式刚好等于:
于是,第一项式子就是第二节VAE模型架构中第二个损失函数的由来。
接下来求第二项,注意到
上述的这个期望,也就是表明在给定![]() (编码器输出)的情况下
(编码器输出)的情况下![]() (解码器输出)的值尽可能高,这其实就是一个类似于Auto-Encoder的损失函数(方差忽略不计的话):
(解码器输出)的值尽可能高,这其实就是一个类似于Auto-Encoder的损失函数(方差忽略不计的话):
因此,第二项式子就是第二节VAE模型架构中第一个损失函数的由来。
综上,关于VAE模型架构中的理论证明部分至此全部介绍完毕。
简易代码
latent_dim = 2
input_dim = 28 * 28
inter_dim = 256
class VAE(nn.Module):
def __init__(self, input_dim=input_dim, inter_dim=inter_dim, latent_dim=latent_dim):
super(VAE, self).__init__()
elf.encoder = nn.Sequential(
nn.Linear(input_dim, inter_dim),
nn.ReLU(),
nn.Linear(inter_dim, latent_dim * 2),
)
self.decoder = nn.Sequential(
nn.Linear(latent_dim, inter_dim),
nn.ReLU(),
nn.Linear(inter_dim, input_dim),
nn.Sigmoid(),
)
def reparameterise(self, mu, logvar):
epsilon = torch.randn_like(mu)
return mu + epsilon * torch.exp(logvar)
def forward(self, x):
org_size = x.size()
batch = org_size[0]
x = x.view(batch, -1)
h = self.encoder(x)
mu, logvar = h.chunk(2, dim=1)
z = self.reparameterise(mu, logvar)
recon_x = self.decoder(z).view(size=org_size)
return recon_x, mu, logvar
# loss: VAE的损失由重构损失和KL损失组成
kl_loss = lambda mu, logvar: -0.5 * torch.sum(1 + logvar - mu.pow(2) - logvar.exp())
recon_loss = lambda recon_x, x: F.binary_cross_entropy(recon_x, x, size_average=False)四、总结
VAE它本质上就是在我们常规的自编码器的基础上,对encoder的结果(在VAE中对应着计算均值的网络)加上了“高斯噪声”,使得结果decoder能够对噪声有鲁棒性;而那个额外的KL loss(目的是让均值为0,方差为1),事实上就是相当于对encoder的一个正则项,希望encoder出来的东西均有零均值。
那另外一个encoder(对应着计算方差的网络)的作用呢?它是用来动态调节噪声的强度的。直觉上来想,当decoder还没有训练好时(重构误差远大于KL loss),就会适当降低噪声(KL loss增加),使得拟合起来容易一些(重构误差开始下降);反之,如果decoder训练得还不错时(重构误差小于KL loss),这时候噪声就会增加(KL loss减少),使得拟合更加困难了(重构误差又开始增加),这时候decoder就要想办法提高它的生成能力了。
说白了,重构的过程是希望没噪声的,而KL loss则希望有高斯噪声的,两者是对立的。所以,VAE跟GAN一样,内部其实是包含了一个对抗的过程,只不过它们两者是混合起来,共同进化的。