【unity c#】程序化网格生成基础
可能很多想入行的新人都已经开始接触houdini的那一套pcg生成案例,这次主要是学习基于unity c#的程序化网格生成。
程序化生成(或者在本篇笔记中,我更倾向于称之为程序化网格)的本质,就是实现对点线面几何数据的操作,不同的工具间最多的接口和封装有区别,底层思维上应该还是相似的。
希望大家也能够有所收获。
程序化生成网格
从概念上讲,三维模型最终都会以网格的形式导入各类渲染引擎,而网格又是由一系列顶点,和连接不同顶点间的三角面构成的。
由于三角形是平的,有直边,它们可以用来完美地呈现平面和直边的东西,比如立方体的表面。弯曲或圆形的表面只能通过使用许多小三角形来近似。如果三角形看起来足够小——不超过一个像素——那么你就不会注意到近似值。通常,这对于实时性能来说是不可行的,因此曲面在某种程度上总是会出现锯齿状。
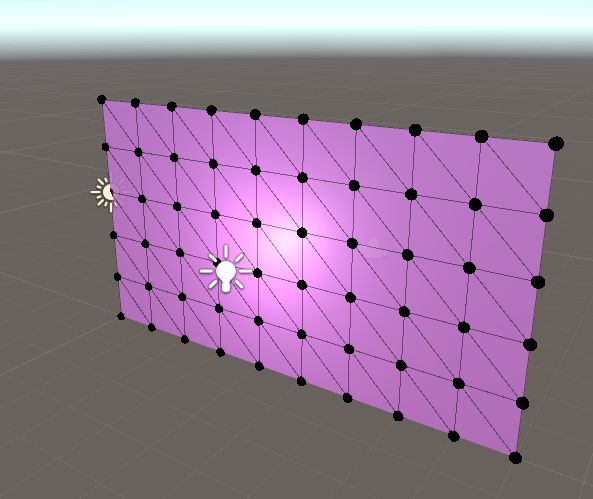
1. 创建平面网格
使模型可见,需要两大基本要素:即网格和材质。
对于网格来说,基础则是顶点。我们先从顶点开始进行绘制:
这里我们使用gizmos类的draw方法进行绘制,注意绘制的结果只能在scene视图里看到,game里面是看不到的。
public class Grid : MonoBehaviour
{
public int xSize, ySize;
public Vector3[] vertices;
public void Awake(){
Generate();
}
private void Generate(){
vertices = new Vector3[(xSize + 1)*(ySize + 1)];
for (int i = 0, y = 0; y <= ySize; y++) {
for (int x = 0; x <= xSize; x++, i++) {
vertices[i] = new Vector3(x, y);
}
}
}
private void OnDrawGizmos(){
Gizmos.color = Color.black;
if(vertices == null){
Debug.Log("vertices is null");
return;
}
for (int i =0; i< vertices.Length; i++){
Gizmos.DrawSphere(vertices[i], 0.1f);
}
}
}
那如果我们想要他们在逐帧里逐个出现呢?
比如说我们直接写多上几个public变量记录当前读取的粒子序号,然后在update里逐个画出?
也不是不行,但是在update里实现的话,就需要一个额外的public向量,来记录当前draw的粒子序号。如果是更复杂的,需要等待上一步执行完毕顺序性逻辑呢?这样会导致update里面会有非常庞大的状态机。
这里我们采用协程的方法来实现。通过协程来实现,就能避免繁琐的状态管理问题。
简单来说,使用协程就三步:
1)调用的时候要套一个StartCoroutine();
2)对应的协程函数,声明类型改为IEnumerator
3)中断执行的地方,写yield return ;
参考unity doc里面对协程的描述和案例参考:unity doc coroutine
public void Awake()
{
StartCoroutine(Generate());
}
private IEnumerator Generate()
{
//今天的shift tab比较反常,就先不对齐了
vertices = new Vector3[(xSize + 1)*(ySize + 1)];
for (int i = 0, y = 0; y <= ySize; y++) {
for (int x = 0; x <= xSize; x++, i++) {
vertices[i] = new Vector3(x, y);
yield return new WaitForSeconds(0.08f);
}
}
}
有了顶点,我们必然就要想办法组成面。
首先我们要创建mesh,把顶点组赋予给mesh,然后指定创建面的顶点顺序,就可以生成我们的第一个三角面了。
1.1 创建基本三角面
public class Grid : MonoBehaviour
{
public int xSize, ySize;
public Vector3[] vertices;
private Mesh mesh;
//其他部分不变
private IEnumerator Generate(){
vertices = new Vector3[(xSize + 1)*(ySize + 1)];
GetComponent<MeshFilter>().mesh = mesh = new Mesh();
// mesh = new Mesh();
mesh.name = "Procedural Grid Plane";
for (int i = 0, y = 0; y <= ySize; y++) {
for (int x = 0; x <= xSize; x++, i++) {
vertices[i] = new Vector3(x, y, 0);
yield return new WaitForSeconds(0.01f);
}
}
// 赋予网格顶点组
mesh.vertices = vertices;
// 通过triangles数组,记录对应的的组成三角面的顶点顺序
int[] triangles = new int[3];
triangles[0] = xSize + 1;
triangles[1] = 1;
triangles[2] = 0;
mesh.triangles = triangles;
}
}
要注意的两点:
1)关于三角面的正反区别:组成面的三个顶点,从当前的视角下观察,顺时针顺序组成的面,为正面,逆时针顺序组成的面,为反面。

2) 关于局部坐标:生成的三角面,是处在以绑定grid.script的game object当前的坐标为原点的局部空间。但是我们设置顶点组所赋予的位置是世界空间,要注意game object的坐标也得是世界原点。


//同理,更新两个三角面
int[] triangles = new int[6];
triangles[0] = xSize + 1;
triangles[1] = 1;
triangles[2] = 0;
triangles[3] = triangles[0];
triangles[4] = triangles[0] + 1;
triangles[5] = 1;
mesh.triangles = triangles;

接下来写一个适用于循环的,注意涉及到行,列递进的部分,要仔细处理清楚。尤其是创建顶点的时候做了xsize, ysize的增加,很容易出错。强烈建议大家都手推一下,这里可以有很多种写法。
//其他部分不变
// 通过triangles数组,记录对应的的组成三角面的顶点顺序
int[] triangles = new int[xSize * ySize * 6];
int tag = 0;
for (int i = 0; i < ySize; i++)
{
for (int j = 0; j< xSize; j++)
{
triangles[tag] = (xSize + 1) * (i + 1) + j ;
triangles[tag + 1] = (xSize + 1) * i + j + 1;
triangles[tag + 2] = (xSize + 1)* i + j;
triangles[tag + 3] = triangles[tag];
triangles[tag + 4] = triangles[tag] + 1;
triangles[tag + 5] = triangles[tag + 1];
tag += 6;
//使面建立也有渐进效果,这里把更新triangles的部分提前到循环里面
mesh.triangles = triangles;
yield return new WaitForSeconds(0.05f);
}
}
效果如下:(这里白色材质是录制动图的问题)
1.2 计算法线
计算法线很简单,直接调用方法即可:
很复杂的法线,最好还是在dcc里面搞。
//完成创建面的迭代之后
mesh.RecalculateNormals();
1.3 赋予uv
在建立顶点组时,同样赋予uv坐标。平面的uv坐标很好理解,直接按百分比去除算,记得要做浮点数的转换。
//.........
Vector2[] uv = new Vector2[vertices.Length];
for (int i = 0, y = 0; y <= ySize; y++) {
for (int x = 0; x <= xSize; x++, i++) {
vertices[i] = new Vector3(x, y, 0);
uv[i] = new Vector2((float)x/xSize, (float)y/ySize);
//同理也可以赋予tangents
//tangents[i] = new Vector4(1f, 0f, 0f, -1f);
yield return new WaitForSeconds(0.01f);
}
}
// 赋予网格顶点组
mesh.vertices = vertices;
mesh.uv = uv;
2. 创建立方体网格
那么来到创建3d cube mesh的情况下,问题就会复杂一些了。
2.1 建立顶点集
首先就是要确定顶点数的问题。
对于一个立方体来说,我们可以把他们拆分为:
1)上下两个完整面(即1.1中的平面):共2个
2)纯边长的面(即无内填顶点的面):共ySize - 1个
那么总顶点数就很显而易见了:
totalVertexs = 2 * (xSize + 1)*(zSize + 1) + (ySize - 1) * (xSize + zSize) * 2;

那么绘制的方法也不难,这里我们主要分为三部分。
1)对于y=0或y=ySize(底面和顶点),我们使用平面一样的方法来绘制
2)对侧面,我们采用仅绘制侧面点的方法来绘制,不做中间填充:
2.1)对于z轴上的两个侧面(z=0或z=zSize),仍能够采用平面绘制的方法
2.2)对于x轴上的两个侧面,只需要绘制两点
int totalVertexs = 2 * (xSize + 1)*(zSize + 1) + (ySize - 1) * (xSize + zSize) * 2;
vertices = new Vector3[totalVertexs];
mesh.name = "Procedural Grid Plane";
for (int i = 0, y = 0; y <= ySize; y++)
{
for (int z = 0; z <= zSize; z++)
{
for (int x = 0; x <= xSize; x++, i++)
{
if(y == 0 || y == ySize){
vertices[i] = new Vector3(x, y, z);
}
else{
if (z == 0 || z == zSize){
vertices[i] = new Vector3(x, y, z);
}
else{
vertices[i] = new Vector3(x, y, z);
x += xSize - 1;
}
}
yield return new WaitForSeconds(0.01f);
}
}
}
2.2 生成面
实际上,3d条件下的面生成没有这么复杂。总的来说就是需要计算好:
1)每一个面的起始节点序号
2)单个面的循环内,每一次换行的节点序号会如何变化
3)每一个面对应的三角朝向
另外比较建议用逐面生成(即各个面单独一个循环来做生成,分为6个重建面的过程)的方法,比一个三层大循环套起来好处理很多。
简单的示意图如下,其实比较麻烦的情况就是从底面到中间面,从中间面到顶面这个地方,由于其层间节点数有差异,所以去求解对应的顶点序号会有不同,处理起来比较麻烦。

下面给大家看一下我的屎山代码,注意只有y = ySize和z = zSize这两个面,我用逐面生成的方法来写了(仅参考最后两个循环即可),其他都是扔到三层大循环里面来做条件判断。。。真的给我干吐了。
private IEnumerator GenerateFaces(){
// 通过triangles数组,记录对应的的组成三角面的顶点顺序
int[] triangles = new int[(xSize * ySize * 2 + xSize * zSize * 2 + ySize * zSize *2) * 6];
int tag = 0;
// 这三个嵌套循环已经成为屎山 千万别碰
for (int y = 0; y < ySize; y++){
for (int z = 0; z < zSize; z++)
{
for (int x = 0; x< xSize; x++)
{
if (y == 0){
// 注意的是,底面和顶面的朝向相反,所以顶点顺序不一样,这里不能统一来处理
triangles[tag] = (xSize + 1) * (z + 1) + x ;
triangles[tag + 1] = (xSize + 1)* z + x;
triangles[tag + 2] = (xSize + 1) * (z + 1) + x + 1;
triangles[tag + 3] = triangles[tag + 1];
triangles[tag + 4] = triangles[tag + 3] + 1;
triangles[tag + 5] = triangles[tag] + 1;
tag += 6;
}
else if(z == 0){ //y!= 0 and z = 0
//处理z轴上的两个面
// z = zSize的情况单独在循环外处理
if (y == 1){
Debug.Log(tag);
Debug.Log($"x: {x}, y: {y}, z: {z}");
triangles[tag] = (xSize + 1) * (zSize + 1) + (y - 1) * (xSize + zSize) * 2 + x;
triangles[tag+1] = triangles[tag] - (xSize + 1) * (zSize + 1) - (y - 1) * (xSize + zSize) * 2 + 1;
triangles[tag+2] = triangles[tag] - (xSize + 1) * (zSize + 1) - (y - 1) * (xSize + zSize) * 2;
triangles[tag+3] = triangles[tag];
triangles[tag + 4] = triangles[tag] + 1;
triangles[tag + 5] = triangles[tag + 1];
Debug.Log($"v1: {triangles[tag]}, v2: {triangles[tag+1]}, v3: {triangles[tag+2]}");
tag += 6;
}
else{
Debug.Log(tag);
Debug.Log($"x: {x}, y: {y}, z: {z}");
triangles[tag] = (xSize + 1) * (zSize + 1) + (y - 1) * (xSize + zSize) * 2 + x;
triangles[tag+1] = triangles[tag] - (xSize + zSize) * 2 + 1;
triangles[tag+2] = triangles[tag] - (xSize + zSize) * 2;
triangles[tag+3] = triangles[tag];
triangles[tag + 4] = triangles[tag] + 1;
triangles[tag + 5] = triangles[tag + 1];
Debug.Log($"v1: {triangles[tag]}, v2: {triangles[tag+1]}, v3: {triangles[tag+2]}");
tag += 6;
if(y == ySize - 1){
//取 y != 1的处理方法,进行调整
Debug.Log(tag);
Debug.Log($"x: {x}, y: {y}, z: {z}");
triangles[tag] = (xSize + 1) * (zSize + 1) + (y) * (xSize + zSize) * 2 + x;
triangles[tag+1] = triangles[tag] - (xSize + zSize) * 2 + 1;
triangles[tag+2] = triangles[tag] - (xSize + zSize) * 2;
triangles[tag+3] = triangles[tag];
triangles[tag + 4] = triangles[tag] + 1;
triangles[tag + 5] = triangles[tag + 1];
Debug.Log($"v1: {triangles[tag]}, v2: {triangles[tag+1]}, v3: {triangles[tag+2]}");
tag += 6;
}
}
}
else{//z != 0 and y != 0
if(y == 1 && z == 1){
// Debug.Log(tag);
Debug.Log($"x: {x}, y: {y}, z: {z}");
triangles[tag] = (xSize + 1) * (zSize + 1) + (y - 1) * (xSize + zSize) * 2 + xSize + 2 * (z - 1) + 1;
triangles[tag + 1] = (xSize + 1) * (zSize + 1) + (y - 1) * (xSize + zSize) * 2 + 2 * (z - 1);
triangles[tag + 2] = (y - 1) * (xSize + zSize) * 2 + xSize * z + 1;
triangles[tag + 3] = triangles[tag + 1];
triangles[tag + 4] = triangles[tag + 2] - (xSize + 1);
triangles[tag + 5] = triangles[tag + 2];
Debug.Log($"v1: {triangles[tag]}, v2: {triangles[tag+1]}, v3: {triangles[tag+2]}");
tag += 6;
//使x = 0 或 x = xSize, 确保每次建面都位于x轴上的两个侧面上
x += xSize;
}
else if(y == 1){
// Debug.Log(tag);
Debug.Log($"x: {x}, y: {y}, z: {z}");
triangles[tag] = (xSize + 1) * (zSize + 1) + (y - 1) * (xSize + zSize) * 2 + xSize + 1 + 2 * (z - 1) ;
triangles[tag + 1] = (xSize + 1) * (zSize + 1) + (y - 1) * (xSize + zSize) * 2 + xSize + 1 + 2 * (z - 2);
triangles[tag + 2] = (y - 1) * (xSize + zSize) * 2 + (xSize + 1) * z;
triangles[tag + 3] = triangles[tag + 1];
triangles[tag + 4] = triangles[tag + 2] - (xSize + 1);
triangles[tag + 5] = triangles[tag + 2];
Debug.Log($"v1: {triangles[tag]}, v2: {triangles[tag+1]}, v3: {triangles[tag+2]}");
tag += 6;
if(z == zSize - 1){
Debug.Log($"final z value building faces for x: {x}, y: {y}, z: {z}");
triangles[tag] = (xSize + 1) * (zSize + 1) + (y - 1) * (xSize + zSize) * 2 + xSize + 1 + 2 * (z) ;
triangles[tag + 1] = (xSize + 1) * (zSize + 1) + (y - 1) * (xSize + zSize) * 2 + xSize + 1 + 2 * (z - 1);
triangles[tag + 2] = (y - 1) * (xSize + zSize) * 2 + (xSize + 1) * (z + 1);
triangles[tag + 3] = triangles[tag + 1];
triangles[tag + 4] = triangles[tag + 2] - (xSize + 1);
triangles[tag + 5] = triangles[tag + 2];
Debug.Log($"v1: {triangles[tag]}, v2: {triangles[tag+1]}, v3: {triangles[tag+2]}");
tag += 6;
}
x += xSize;
}
else{ // y!= 1 and z != 0 and y != 0
if(z == 1){
Debug.Log($"x: {x}, y: {y}, z: {z}");
triangles[tag] = (xSize + 1) * (zSize + 1) + (y - 1) * (xSize + zSize) * 2 + xSize + 1 + 2 * (z - 1) ;
triangles[tag + 1] = (xSize + 1) * (zSize + 1) + (y - 1) * (xSize + zSize) * 2 + 2 * (z - 1);
triangles[tag + 2] = (xSize + 1) * (zSize + 1) + (y - 2) * (xSize + zSize) * 2 + xSize + 1 + 2 * (z - 1);
triangles[tag + 3] = triangles[tag + 1];
triangles[tag + 4] = triangles[tag + 2] - (xSize + 1);
triangles[tag + 5] = triangles[tag + 2];
Debug.Log($"v1: {triangles[tag]}, v2: {triangles[tag+1]}, v3: {triangles[tag+2]}");
tag += 6;
if(y == ySize - 1){
Debug.Log($"y = ySize -1, z = 1; x: {x}, y: {y}, z: {z}");
triangles[tag] = (xSize + 1) * (zSize + 1) + (y - 1) * (xSize + zSize) * 2 + xSize + 1 + 2 * (z - 1) ;
triangles[tag + 1] = (xSize + 1) * (zSize + 1) + (y) * (xSize + zSize) * 2 + z * (xSize + 1) ;
triangles[tag + 2] = triangles[tag + 1] - xSize - 1;
triangles[tag + 3] = triangles[tag + 2];
triangles[tag + 4] = triangles[tag] - xSize - 1;
triangles[tag + 5] = triangles[tag];
Debug.Log($"v1: {triangles[tag]}, v2: {triangles[tag+1]}, v3: {triangles[tag+2]}");
tag += 6;
}
x += xSize;
}
else{
Debug.Log($"x: {x}, y: {y}, z: {z}");
triangles[tag] = (xSize + 1) * (zSize + 1) + (y - 1) * (xSize + zSize) * 2 + xSize + 1 + 2 * (z - 1) ;
triangles[tag + 1] = (xSize + 1) * (zSize + 1) + (y - 1) * (xSize + zSize) * 2 + xSize + 1 + 2 * (z - 2);
triangles[tag + 2] = (xSize + 1) * (zSize + 1) + (y - 2) * (xSize + zSize) * 2 + xSize + 1 + 2 * (z - 1);
triangles[tag + 3] = triangles[tag + 1];
triangles[tag + 4] = triangles[tag + 2] - 2;
triangles[tag + 5] = triangles[tag + 2];
Debug.Log($"v1: {triangles[tag]}, v2: {triangles[tag+1]}, v3: {triangles[tag+2]}");
tag += 6;
//由于循环内x,y,z都不会取到最后一列顶点
//如果z = zSize - 1,则做两次建面,左侧一次,右侧一次
if(z == zSize - 1){
Debug.Log($"final z value building faces for x: {x}, y: {y}, z: {z}");
triangles[tag] = (xSize + 1) * (zSize + 1) + (y - 1) * (xSize + zSize) * 2 + xSize + 1 + 2 * (z) ;
triangles[tag + 1] = (xSize + 1) * (zSize + 1) + (y - 1) * (xSize + zSize) * 2 + xSize + 1 + 2 * (z - 1);
triangles[tag + 2] = (xSize + 1) * (zSize + 1) + (y - 2) * (xSize + zSize) * 2 + xSize + 1 + 2 * (z);
triangles[tag + 3] = triangles[tag + 1];
triangles[tag + 4] = triangles[tag + 2] - 2;
triangles[tag + 5] = triangles[tag + 2];
Debug.Log($"v1: {triangles[tag]}, v2: {triangles[tag+1]}, v3: {triangles[tag+2]}");
tag += 6;
}
if(y == ySize - 1){
Debug.Log($"x: {x}, y: {y}, z: {z}");
triangles[tag] = (xSize + 1) * (zSize + 1) + (y - 1) * (xSize + zSize) * 2 + xSize + 1 + 2 * (z - 1) ;
triangles[tag + 1] = (xSize + 1) * (zSize + 1) + (y) * (xSize + zSize) * 2 + (z - 1) * (xSize + 1);
triangles[tag + 2] = triangles[tag] - 2;
triangles[tag + 3] = triangles[tag];
triangles[tag + 4] = triangles[tag + 1] + xSize + 1;
triangles[tag + 5] = triangles[tag + 1];
Debug.Log($"v1: {triangles[tag]}, v2: {triangles[tag+1]}, v3: {triangles[tag+2]}");
tag += 6;
if(z == zSize -1){
Debug.Log($"final z value building faces for x: {x}, y: {y}, z: {z}");
triangles[tag] = (xSize + 1) * (zSize + 1) + (y - 1) * (xSize + zSize) * 2 + xSize + 1 + 2 * (z - 1) ;
triangles[tag + 1] = triangles[tag] + 2;
triangles[tag + 2] = (xSize + 1) * (zSize + 1) + (y) * (xSize + zSize) * 2 + z * (xSize + 1) ;
triangles[tag + 3] = triangles[tag + 1];
triangles[tag + 4] = triangles[tag + 2] + xSize + 1;
triangles[tag + 5] = triangles[tag + 2];
Debug.Log($"v1: {triangles[tag]}, v2: {triangles[tag+1]}, v3: {triangles[tag+2]}");
tag += 6;
}
}
x += xSize;
}
}
if(x == xSize){
if(y == 1 && z == 1){
Debug.Log($"x: {x}, y: {y}, z: {z}");
triangles[tag] = (xSize + 1) * (zSize + 1) + (y - 1) * (xSize + zSize) * 2 + xSize + 2 * (z - 1) + 2;
triangles[tag + 1] = (y - 1) * (xSize + zSize) * 2 + xSize * z + 1 + xSize;
triangles[tag + 2] = (xSize + 1) * (zSize + 1) + (y - 1) * (xSize + zSize) * 2 + xSize + 2 * (z - 1) ;
triangles[tag + 3] = triangles[tag + 2];
triangles[tag + 4] = triangles[tag + 1];
triangles[tag + 5] = triangles[tag + 1] - (xSize + 1);
Debug.Log($"v1: {triangles[tag]}, v2: {triangles[tag+1]}, v3: {triangles[tag+2]}");
tag += 6;
}
else if(y == 1){
Debug.Log($"x: {x}, y: {y}, z: {z}");
triangles[tag] = (xSize + 1) * (zSize + 1) + (y - 1) * (xSize + zSize) * 2 + xSize + 2 + 2 * (z - 1) ;
triangles[tag + 1] = (y - 1) * (xSize + zSize) * 2 + (xSize + 1) * z + x;
triangles[tag + 2] = (xSize + 1) * (zSize + 1) + (y - 1) * (xSize + zSize) * 2 + xSize + 2 * (z - 1) ;
triangles[tag + 3] = triangles[tag + 2];
triangles[tag + 4] = triangles[tag + 1];
triangles[tag + 5] = triangles[tag + 1] - (xSize + 1);
Debug.Log($"v1: {triangles[tag]}, v2: {triangles[tag+1]}, v3: {triangles[tag+2]}");
tag += 6;
if (z == zSize - 1){
Debug.Log($"final z value building faces for x: {x}, y: {y}, z: {z}");
triangles[tag] = (xSize + 1) * (zSize + 1) + (y - 1) * (xSize + zSize) * 2 + xSize + 2 + 2 * (z - 1) + xSize + 1;
triangles[tag + 1] = (y - 1) * (xSize + zSize) * 2 + (xSize + 1) * z + x + xSize + 1;
triangles[tag + 2] = (xSize + 1) * (zSize + 1) + (y - 1) * (xSize + zSize) * 2 + xSize + 2 * (z) ;
triangles[tag + 3] = triangles[tag + 2];
triangles[tag + 4] = triangles[tag + 1];
triangles[tag + 5] = triangles[tag + 1] - (xSize + 1);
Debug.Log($"v1: {triangles[tag]}, v2: {triangles[tag+1]}, v3: {triangles[tag+2]}");
tag += 6;
}
}
else{
if(z == 1){
Debug.Log(tag);
Debug.Log($"x: {x}, y: {y}, z: {z}");
triangles[tag] = (xSize + 1) * (zSize + 1) + (y - 2) * (xSize + zSize) * 2 + xSize + 2 + 2 * (z - 1);
triangles[tag + 1] = (xSize + 1) * (zSize + 1) + (y - 1) * (xSize + zSize) * 2 + xSize + 2 + 2 * (z - 2);
triangles[tag + 2] = (xSize + 1) * (zSize + 1) + (y - 1) * (xSize + zSize) * 2 + xSize + 2 + 2 * (z - 1) ;
triangles[tag + 3] = triangles[tag];
triangles[tag + 4] = triangles[tag] - 2;
triangles[tag + 5] = triangles[tag + 1];
Debug.Log($"v1: {triangles[tag]}, v2: {triangles[tag+1]}, v3: {triangles[tag+2]}");
tag += 6;
if(y == ySize -1){
Debug.Log($"y = ySize -1, z = 1; x: {x}, y: {y}, z: {z}");
triangles[tag] = (xSize + 1) * (zSize + 1) + (y - 1) * (xSize + zSize) * 2 + xSize + 2 + 2 * (z - 1) ;
triangles[tag + 1] = (xSize + 1) * (zSize + 1) + (y) * (xSize + zSize) * 2 + z * (xSize);
triangles[tag + 2] = triangles[tag + 1] + xSize + 1;
triangles[tag + 3] = triangles[tag];
triangles[tag + 4] = triangles[tag] - 2;
triangles[tag + 5] = triangles[tag + 1];
Debug.Log($"v1: {triangles[tag]}, v2: {triangles[tag+1]}, v3: {triangles[tag+2]}");
tag += 6;
}
}
else{
Debug.Log(tag);
Debug.Log($"x: {x}, y: {y}, z: {z}");
triangles[tag] = (xSize + 1) * (zSize + 1) + (y - 1) * (xSize + zSize) * 2 + xSize + 2 + 2 * (z - 1) ;
triangles[tag + 1] = (xSize + 1) * (zSize + 1) + (y - 2) * (xSize + zSize) * 2 + xSize + 2 + 2 * (z - 1);
triangles[tag + 2] = (xSize + 1) * (zSize + 1) + (y - 1) * (xSize + zSize) * 2 + xSize + 2 + 2 * (z - 2);
triangles[tag + 3] = triangles[tag + 2];
triangles[tag + 4] = triangles[tag + 1];
triangles[tag + 5] = triangles[tag + 1] - 2;
Debug.Log($"v1: {triangles[tag]}, v2: {triangles[tag+1]}, v3: {triangles[tag+2]}");
tag += 6;
if(z == zSize - 1){
Debug.Log($"final z value building faces for x: {x}, y: {y}, z: {z}");
triangles[tag] = (xSize + 1) * (zSize + 1) + (y - 1) * (xSize + zSize) * 2 + xSize + 2 + 2 * (z - 1) + xSize + 1;
triangles[tag + 1] = (xSize + 1) * (zSize + 1) + (y - 2) * (xSize + zSize) * 2 + xSize + 2 + 2 * (z - 1) + xSize + 1;
triangles[tag + 2] = (xSize + 1) * (zSize + 1) + (y - 1) * (xSize + zSize) * 2 + xSize + 2 + 2 * (z - 1);
triangles[tag + 3] = triangles[tag + 2];
triangles[tag + 4] = triangles[tag + 1];
triangles[tag + 5] = triangles[tag + 1] - xSize - 1;
Debug.Log($"v1: {triangles[tag]}, v2: {triangles[tag+1]}, v3: {triangles[tag+2]}");
tag += 6;
}
if(y == ySize -1){
Debug.Log($"y = ySize -1, z = 1; x: {x}, y: {y}, z: {z}");
triangles[tag] = (xSize + 1) * (zSize + 1) + (y - 1) * (xSize + zSize) * 2 + xSize + 2 + 2 * (z - 1) ;
triangles[tag + 1] = (xSize + 1) * (zSize + 1) + (y) * (xSize + zSize) * 2 + (z) * (xSize + 1) - 1;
triangles[tag + 2] = triangles[tag + 1] + xSize + 1;
triangles[tag + 3] = triangles[tag];
triangles[tag + 4] = triangles[tag] - 2;
triangles[tag + 5] = triangles[tag + 1];
Debug.Log($"v1: {triangles[tag]}, v2: {triangles[tag+1]}, v3: {triangles[tag+2]}");
tag += 6;
if(z == zSize -1){
Debug.Log($"y = ySize -1, z = 1; x: {x}, y: {y}, z: {z}");
triangles[tag] = (xSize + 1) * (zSize + 1) + (y - 1) * (xSize + zSize) * 2 + xSize + 2 + 2 * (z - 1) ;
triangles[tag + 1] = (xSize + 1) * (zSize + 1) + (y) * (xSize + zSize) * 2 + (z + 1) * (xSize + 1) - 1;
triangles[tag + 2] = triangles[tag] + xSize + 1;
triangles[tag + 3] = triangles[tag + 1];
triangles[tag + 4] = triangles[tag + 1] + xSize + 1;
triangles[tag + 5] = triangles[tag + 2];
Debug.Log($"v1: {triangles[tag]}, v2: {triangles[tag+1]}, v3: {triangles[tag+2]}");
tag += 6;
}
}
}
}
}
}
mesh.triangles = triangles;
yield return new WaitForSeconds(0.05f);
}
}
}
Debug.Log(tag);
yield return new WaitForSeconds(0.5f);
//对顶面进行面构建,请参考这个以及以下的循环
int FaceTag = ySize;
int startVertex = (xSize + 1) * (zSize + 1) + (ySize - 1) * (xSize + zSize) * 2;
// tag = startVertex * 6;
for(int z = 0; z < zSize; z++){
for(int x = 0; x<= xSize; x++){
if (x == xSize){
continue;
}
triangles[tag] = startVertex + x + z * (xSize + 1);
triangles[tag + 1] = triangles[tag] + xSize + 1;
triangles[tag + 2] = triangles[tag + 1] + 1;
triangles[tag + 3] = triangles[tag];
triangles[tag + 4] = triangles[tag + 2];
triangles[tag + 5] = triangles[tag] + 1;
tag += 6;
Debug.Log($"y = ySize; x: {x}, z: {z}, startVertex:{startVertex + x + z * xSize}");
mesh.triangles = triangles;
yield return new WaitForSeconds(0.05f);
}
}
//z = zSize面
startVertex = zSize * (xSize + 1);
for(int y = 0; y < ySize; y++){
for(int x = 0; x<= xSize; x++){
if(x == xSize){
continue;
}
if(y != ySize - 1){
triangles[tag] = startVertex + x + y * 2 * (xSize + zSize);
triangles[tag + 1] = triangles[tag] + 1;
triangles[tag + 2] = startVertex + x + (y + 1) * 2 * (xSize + zSize);
triangles[tag + 3] = triangles[tag + 2];
triangles[tag + 4] = triangles[tag + 1] ;
triangles[tag + 5] = triangles[tag + 2] + 1;
tag += 6;
Debug.Log($"y = ySize;tag:{tag}, x: {x}, y: {y}, startVertex:{startVertex + x + y * 2 * (xSize + zSize)}");
Debug.Log($"v1:{triangles[tag]}, v2:{triangles[tag+1]}, v3:{triangles[tag+2]}");
yield return new WaitForSeconds(0.05f);
mesh.triangles = triangles;
}
else{
triangles[tag] = startVertex + x + y * 2 * (xSize + zSize);
triangles[tag + 1] = triangles[tag] + 1;
triangles[tag + 2] = startVertex + x + (y) * 2 * (xSize + zSize) + (xSize + 1) * (zSize + 1);
triangles[tag + 3] = triangles[tag + 2];
triangles[tag + 4] = triangles[tag + 1] ;
triangles[tag + 5] = triangles[tag + 2] + 1;
tag += 6;
if (tag >= (xSize * ySize * 2 + xSize * zSize * 2 + ySize * zSize *2) * 6){
mesh.triangles = triangles;
break;
}
Debug.Log($"y = ySize;tag:{tag}, x: {x}, y: {y}, startVertex:{startVertex + x + y * 2 * (xSize + zSize)}");
Debug.Log($"v1:{triangles[tag]}, v2:{triangles[tag+1]}, v3:{triangles[tag+2]}");
yield return new WaitForSeconds(0.05f);
mesh.triangles = triangles;
}
}
}
// mesh.triangles = triangles;
// mesh.RecalculateNormals();
}

另外,上述的写法仍存在bug,这种庞大循环套条件处理的方法,对于y小于等于2,xsize,zsize都为1的情况下,由于缺少对应的处理逻辑,会导致失灵,而单个面构建(顶面和z = zSize面)的方法则没有这种bug。


调整为6个面单独构建后,bug的问题解决,现在可以建立1x1x1的网格了。

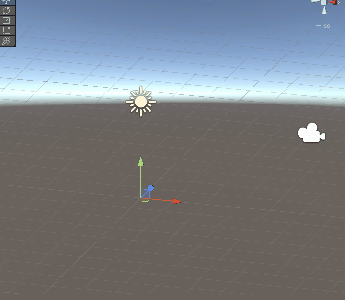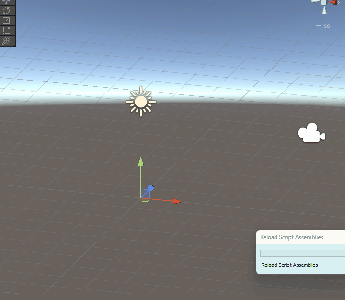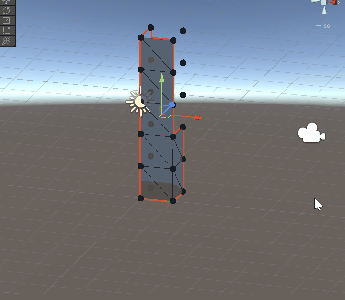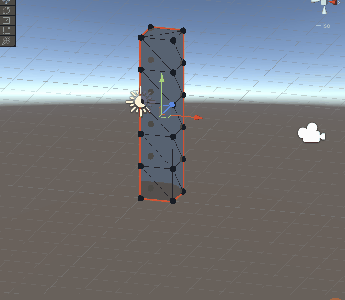
3. 建立圆角立方体网格
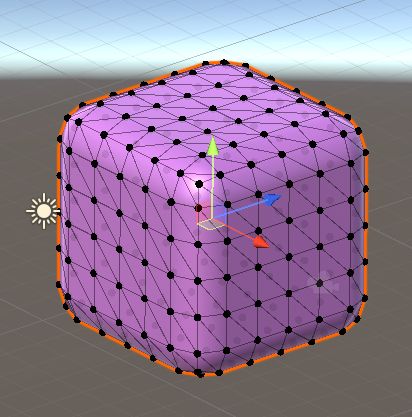
为了实现圆角立方体的构建,我们需要去调整边缘部分的顶点的位置。这里我们增加一个新参数:roundness。
它的物理意义是圆角的柔和程度,不过在取值上不是0-1,而是具体要被圆滑的顶点数,被圆滑的顶点越多,则圆滑程度越大。
当然也有前提,一是立方体本身顶点数不能过少,二是平滑的程度也不能大于对应边的顶点数的一半。
主要还是基于六个面做成面,所以成面方式还是不变,改变的主要是成点的方法。
基于需要进行圆角调整的顶点,主要是位置属于以下三类顶点:
1)x < roundness or x > xSize - roundness
2)y < roundness or y > ySize - roundness
3) z < roundness or z > zSize - roundness
先基于符合范围的外部顶点,向内坍缩出内部顶点,再由外部顶点减内部顶点求得法线,基于法线对内部顶点进行偏移。
private void GenerateVertexs(){
vertices = new Vector3[totalVertexs];
normals = new Vector3[totalVertexs];
for (int i = 0, y = 0; y <= ySize; y++)
{
for (int z = 0; z <= zSize; z++)
{
for (int x = 0; x <= xSize; x++, i++)
{
bool marchTag = false;
if(y == 0 || y == ySize){
vertices[i] = new Vector3(x, y, z);
}
else{
if (z == 0 || z == zSize){
vertices[i] = new Vector3(x, y, z);
}
else{
vertices[i] = new Vector3(x, y, z);
marchTag = true;
}
}
Vector3 innerPoint = vertices[i];
if ( x < roundness){
innerPoint.x = roundness;
}
else if( x > xSize - roundness){
innerPoint.x = xSize - roundness;
}
if(y < roundness){
innerPoint.y = roundness;
}
else if(y > ySize - roundness){
innerPoint.y = ySize - roundness;
}
if(z < roundness){
innerPoint.z = roundness;
}
else if(z > zSize - roundness){
innerPoint.z = zSize - roundness;
}
normals[i] = (vertices[i] - innerPoint).normalized;
vertices[i] = innerPoint + roundness * normals[i];
if(marchTag){
x += xSize - 1;
}
}
}
}
// 赋予网格顶点组
mesh.vertices = vertices;
mesh.normals = normals;
// mesh.uv = uv;
// mesh.tangents = tangents;
}
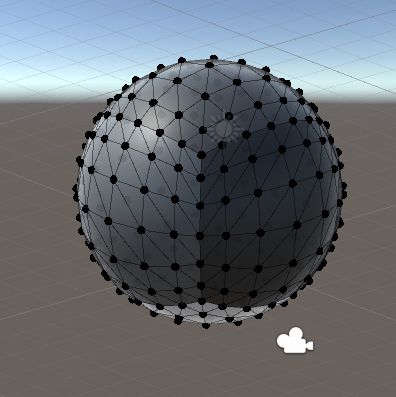
以立方体为例,展示下圆滑程度(1-2-3)的变化带来的效果差异:


3.1 实现逐面拆分
主要通过设置mesh的子mesh数目的方式,并且建立对应的三角序号数组。
// in function : GenerateFaces
int[] triangles = new int[(xSize * ySize * 2 + xSize * zSize * 2 + ySize * zSize *2) * 6];
int tag = 0;
//设置子mesh数目,并同时建立6个字面对应的三角数组
mesh.subMeshCount = 6;
int[] triangles1 = new int[xSize * zSize * 6];
int[] triangles2 = new int[xSize * ySize * 6];
int[] triangles3 = new int[zSize * ySize * 6];
int[] triangles4 = new int[zSize * ySize * 6];
int[] triangles5 = new int[zSize * xSize * 6];
int[] triangles6 = new int[xSize * ySize * 6];
//构建底面,以构建底面的部分为例,构建其他面的处理,处理方法类似
for (int z = 0; z<zSize ; z ++){
for(int x = 0; x<xSize; x++){
triangles[tag] = (xSize + 1) * (z + 1) + x ;
triangles[tag + 1] = (xSize + 1)* z + x;
triangles[tag + 2] = (xSize + 1) * (z + 1) + x + 1;
triangles[tag + 3] = triangles[tag + 1];
triangles[tag + 4] = triangles[tag + 3] + 1;
triangles[tag + 5] = triangles[tag] + 1;
tag += 6;
// mesh.triangles = triangles;
}
}
Array.Copy(triangles, 0, triangles1, 0, triangles1.Length);
mesh.SetTriangles(triangles1, 0);
同样的,我们需要在mesh renderer处设置额外的材质,不然就会出现子网格渲染不出来的情况。

这里我们给六个面做了颜色不一样的材质。

3.2 增加碰撞体
主要是通过立方体+胶囊体的形式,多个碰撞体叠加来完成mesh碰撞体的构建。
配置上,主要分为对应6个平面的3个立方体碰撞体,以及对应8个圆角的4个胶囊体(根据情况可以增加,但建议从简,在这个场景下,就算碰撞体配置的再多,穿模也不可避免)。
private void SizeColliders(float x, float y, float z){
BoxCollider c = gameObject.AddComponent<BoxCollider>();
c.size = new Vector3(x, y, z);
}
private void AddCapsuleCollider (int direction, float x, float y, float z) {
CapsuleCollider c = gameObject.AddComponent<CapsuleCollider>();
c.center = new Vector3(x, y, z);
c.direction = direction;
c.radius = roundness;
c.height = c.center[direction] * 2f;
}
private void GenerateColliders(){
SizeColliders(xSize, ySize - roundness* 2, zSize - roundness * 2);
SizeColliders(xSize - roundness * 2, ySize, zSize - roundness * 2);
SizeColliders(xSize - roundness * 2, ySize - roundness * 2, zSize);
Vector3 min = Vector3.one * roundness;
Vector3 half = new Vector3(xSize, ySize, zSize) * 0.5f;
Vector3 max = new Vector3(xSize, ySize, zSize) - min;
AddCapsuleCollider(0, half.x, min.y, min.z);
AddCapsuleCollider(0, half.x, min.y, max.z);
AddCapsuleCollider(0, half.x, max.y, min.z);
AddCapsuleCollider(0, half.x, max.y, max.z);
}
记得在碰撞体的基础上,赋予刚体,不然碰撞体加了也是没用的。
进行简单的场景搭建,全场景程序化生成的效果如下: