day16 二叉树的最大深度 n叉树的最大深度 二叉树的最小深度 完全二叉树的节点数
题目1:104 二叉树的最大深度
题目链接:104 二叉树的最大深度
题意
二叉树的根节点是root,返回其最大深度(从根节点到最远叶子节点的最长路径上的节点数)
递归
根节点的的高度就是二叉树的最大深度 所以使用后序遍历求最大高度的方式求出最大深度
递归三部曲
1)确定递归函数的参数和返回值
2)确定终止条件
3)确定单层递归的逻辑
代码
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
int result;
int maxDepth(TreeNode* root) {
//终止条件
if(root==NULL) return 0;
//单层递归逻辑 后序遍历 左右中
int leftheight = maxDepth(root->left);//左
int rightheight = maxDepth(root->right);//右
int height = 1 + max(leftheight,rightheight);
return height;
}
};层序遍历
最大深度就是判断二叉树有几层
代码
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
int result;
int maxDepth(TreeNode* root) {
queue que;
if(root!=NULL) que.push(root);
int count = 0;
while(!que.empty()){
int size = que.size();
while(size--){
TreeNode* node = que.front();
que.pop();
if(node->left) que.push(node->left);
if(node->right) que.push(node->right);
}
count++;
}
return count;
}
}; 逻辑
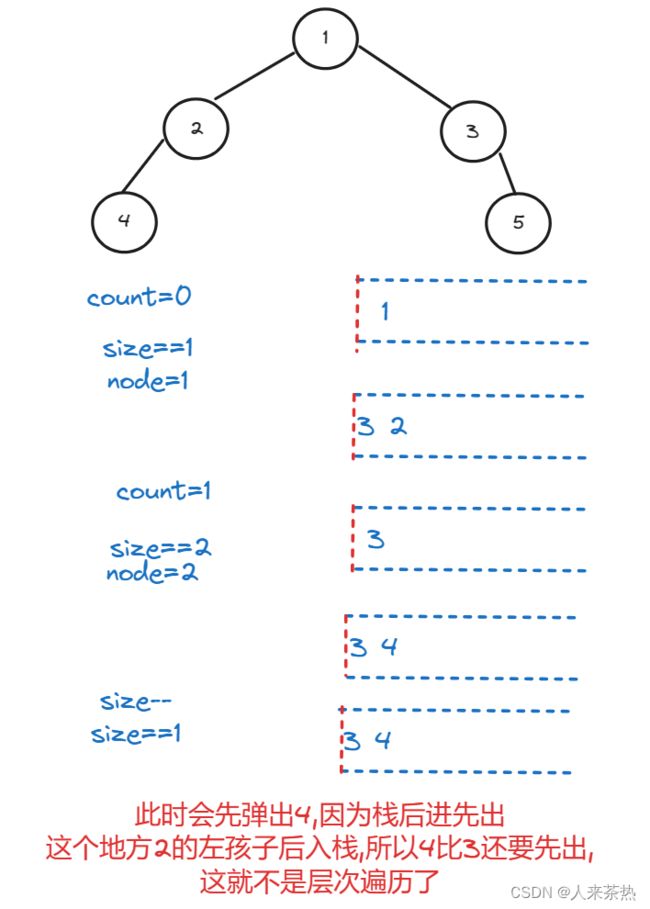
例1:层次遍历只能使用队列不能使用栈,以下是使用栈的反例
题目2:559 n叉树的最大深度
题目链接:555 n叉树的最大深度
题意
n叉树的最大深度
递归(难)
代码
/*
// Definition for a Node.
class Node {
public:
int val;
vector children;
Node() {}
Node(int _val) {
val = _val;
}
Node(int _val, vector _children) {
val = _val;
children = _children;
}
};
*/
class Solution {
public:
int maxDepth(Node* root) {
//终止条件
if(root==NULL) return 0;
//单层递归逻辑 后序遍历 左右中
int depth = 0;
for(int i=0;ichildren.size();i++){
depth = max(depth,maxDepth(root->children[i]));
cout<<"node:"<children[i]->val< 层序遍历
一个node可能有多个孩子
代码
/*
// Definition for a Node.
class Node {
public:
int val;
vector children;
Node() {}
Node(int _val) {
val = _val;
}
Node(int _val, vector _children) {
val = _val;
children = _children;
}
};
*/
class Solution {
public:
int maxDepth(Node* root) {
queue que;
if(root!=NULL) que.push(root);
int count = 0;
while(!que.empty()){
int size = que.size();
while(size--){
Node* node = que.front();
que.pop();
//一个node可能有多个海泽
for(int i=0;ichildren.size();i++){
if(node->children[i]) que.push(node->children[i]);
}
}
count++;
}
return count;
}
}; 题目3:111 二叉树的最小深度
题目链接:111 二叉树的最小深度
题意
根据二叉树的根节点root,找出其最小深度(根节点到最近叶子节点的路径上的节点数量)
递归
递归三部曲:
1)确定递归函数的返回值和参数
2)确定终止条件
3)确定单层递归逻辑
左子树为空,右子树不为空,最小深度是1+右子树的深度
左子树不为空,右子树为空,最小深度是1+左子树的深度
左子树不为空,右子树也不为空,最小深度是左右子树深度最小值+1
代码
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
int minDepth(TreeNode* root) {
//终止条件
if(root==NULL) return 0;
//单层递归逻辑 后序遍历 左右中
int leftheight = minDepth(root->left);//左
int rightheight = minDepth(root->right);//右
//中
if(root->left==NULL && root->right!=NULL) return 1 + rightheight;
if(root->left!=NULL && root->right==NULL) return 1 + leftheight;
int result = 1 + min(rightheight,leftheight);
return result;
}
};层序遍历
遇到一个节点,该节点的左右孩子都为空,才是最终的叶子节点,return height即可
代码
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
int minDepth(TreeNode* root) {
queue que;
int count = 0;
if(root!=NULL) que.push(root);
while(!que.empty()){
int size =que.size();
count++;//这时count必须在前面,不能写在后面,要先加
//如果写在后面,有可能还没有加呢,就直接满足node->left和node->right都为空就直接return了
while(size--){
TreeNode* node = que.front();
que.pop();
if(node->left){
que.push(node->left);
}
if(node->right){
que.push(node->right);
}
if(node->left==NULL && node->right==NULL){
return count;
}
}
}
return count;
}
}; 题目4:222 完全二叉树的节点个数
题目链接:222 完全二叉树的节点个数
题意
根据完全二叉树的根节点root,求出该树的节点个数
递归
递归三部曲
1)确定递归函数的参数和返回值
2)确定终止条件
3)确定单层递归的逻辑
后序遍历
普通二叉树
代码
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
int countNodes(TreeNode* root) {
//终止条件
if(root==NULL) return 0;
//单层递归逻辑 后序遍历 左右中
int leftnum = countNodes(root->left);
int rightnum = countNodes(root->right);
int result = leftnum + rightnum + 1;
return result;
}
};- 时间复杂度:O(n) 遍历了所有节点
- 空间复杂度:O(log n),算上了递归系统栈占用的空间
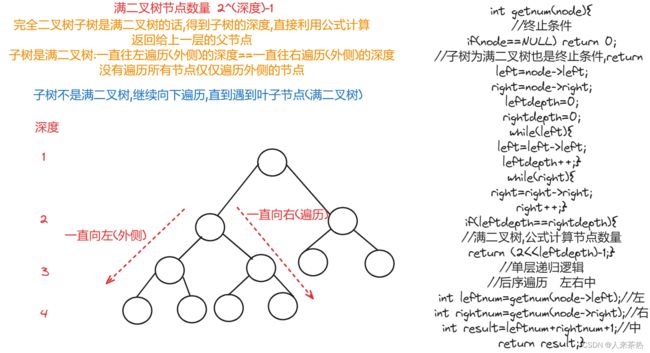
完全二叉树
代码
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
int countNodes(TreeNode* root) {
//终止条件 空节点,子树为满二叉树
if(root==NULL) return 0;//空节点
TreeNode* leftnode = root->left;
TreeNode* rightnode = root->right;
int leftdepth = 0;
int rightdepth = 0;
while(leftnode){
leftnode = leftnode->left;
leftdepth++;
}
while(rightnode){
rightnode = rightnode->right;
rightdepth++;
}
if(leftdepth==rightdepth) return (2<left);
int rightnum = countNodes(root->right);
int result = leftnum + rightnum + 1;
return result;
}
}; - 时间复杂度:O(log n × log n)
- 空间复杂度:O(log n)
层序遍历
可以求任意一个二叉树的节点个数,并没有用上题目中说的完全二叉树的条件
代码
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
int countNodes(TreeNode* root) {
queue que;
if(root!=NULL) que.push(root);
int count = 0;
while(!que.empty()){
int size = que.size();
while(size--){
count++;
TreeNode* node = que.front();
que.pop();
if(node->left) que.push(node->left);
if(node->right) que.push(node->right);
}
}
return count;
}
}; - 时间复杂度:O(n)
- 空间复杂度:O(n)