刷题第一天

1.阶乘求和

令 S = 1! + 2! + 3! + ... + 202320232023! ，求 S 的末尾 9 位数字。

提示：答案首位不为 0 。

很明显,这题如果死算肯定会超出最大数据类型的范围,n∈[1,202320232023],n越大,其中包含10,2,5,的数字(5,12,25,32......)也变多,这些数字相乘末尾为0,这些数字越多,末尾的0也就越多,我们要求最后九位数字,我们就先看看到什么程度的时候最后九位数字都为0,最后我们再求后九位不为0的数的阶乘之和,这样数字范围就不会超标了,所以我们先估计一下大概多少数的阶乘会有9个0,假设50

import java.math.BigInteger;

public class question1 {
    public static void main(String[] args) {
        BigInteger n=new BigInteger("1");
        BigInteger sum=new BigInteger("0");
        for(int i=1;i<50;i++) {
            n=n.multiply(new BigInteger(""+i));
            sum=sum.add(n);
            System.out.println("i="+i+"时，sum后九位是："+sum.mod(new BigInteger(""+1000000000)));
        }
    }
}

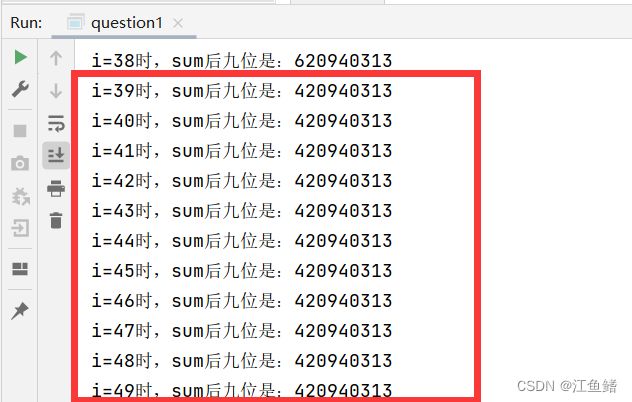
然后我们看运行结果,很明显当i>38,sum的后九位都是维持在420940313,所以这就是结果 

 

http://t.csdnimg.cn/R1h0G      代码借鉴于该链接

2.幸运数字
哈沙德数是指在某个固定的进位制当中，可以被各位数字之和整除的正整数。例如 126 是十进制下的一个哈沙德数，因为 (126)10 mod (1+2+6) = 0；126也是八进制下的哈沙德数，因为 (126)10 = (176)8，(126)10 mod (1 + 7 + 6) = 0；同时 126 也是 16 进制下的哈沙德数，因为 (126)10 = (7e)16，(126)10 mod (7 + e) = 0。小蓝认为，如果一个整数在二进制、八进制、十进制、十六进制下均为哈沙德数，那么这个数字就是幸运数字，第 1 至第 10 个幸运数字的十进制表示为：1 , 2 , 4 , 6 , 8 , 40 , 48 , 72 , 120 , 126 . . . 。现在他想知道第 2023 个幸运数字是多少？你只需要告诉小蓝这个整数的十进制表示即可。
这里简单讲解一下题目,mod 的意思是:a mod b = 0,就是 a ÷ b 的余数为0(怕有不知道的小伙伴,我这里解释一下)

public class {
    public static void main(String[] args) {
        int j=0;
        for (int i=1;i<10000000;i++){
            if (BaseConversion(i)){
                j++;
                if (j==2023){
                    System.out.println(i);//215040
                    break;
                }
            }
        }
    }
    public static boolean BaseConversion(int n){
        //十进制
        int sum=0;
        int x=n;
        while (x!=0){
            sum+=(x%10);
            x/=10;
        }
        if (n%sum!=0)
            return false;
        //二进制
        sum=0;
        x=n;
        while (x!=0){
            sum+=(x%2);
            x/=2;
        }
        if (n%sum!=0)
            return false;
        //八进制
        sum=0;
        x=n;
        while (x!=0){
            sum+=(x%8);
            x/=8;
        }
        if (n%sum!=0)
            return false;
        //十六进制
        int[] arr={0,1,2,3,4,5,6,7,8,9,10,11,12,13,14,15};
        sum=0;
        x=n;
        while (x!=0){
            sum+=(arr[x%16]);
            x/=16;
        }
        if (n%sum!=0)
            return false;
        return true;
    }
}
 

http://t.csdnimg.cn/lARtX    上面代码借鉴于该连接

第三题

这题简单来说就是有一个数组A,从数组中抽出一些数放在 R1 ,剩下的数放在 R2 ,但是R1 和 R2 各自里面的数的总和 S1 和 S2 需要为偶数,比如A中有{1,2,3,4},把2放在R1,R1 的总和 S1 就是2也就是偶数,剩下的1,3,4放在 R2,那 R2 的总和 S2 就等于8也是偶数,这样的情况就是符合条件的,题目要我们一组数据有多少种分配结果能够符合上述条件

当 A 中有奇数个奇数时,不管怎么分配相加,都是不可能达到S1和S2为偶数的,所以这种情况直接输出0

当 A 中有偶数个奇数,假设奇数个数为b,偶数个数为a,那要达到上述情况,R1和R2中分配的数据若有奇数,那么奇数的个数必须为偶数个,而偶数可以随意分配,所以根据排列组合,每个偶数都有两种情况(被选/没被选)那么a个偶数就有2的a次幂种选法,而奇数必须选偶数个,选法如下图所示

然后高中有一个公式是这样的

由于奇数那个式子只选取了公式的一半,结果也就是公式的结果除以2,所以可以化简为2的b-1次幂 

然后2的b-1次幂再和2的a次幂相乘,就能得到所有符合题目条件的分配结果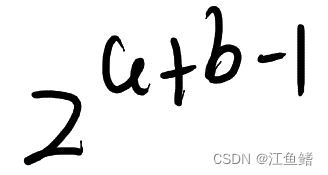

import java.util.Scanner;

public class question2 {
    public static void main(String[] args) {
        Scanner scanner = new Scanner(System.in);
        int t = scanner.nextInt();//先输入t组数据
        while(t--  >0){
            int n = scanner.nextInt();
            int odd = 0;//奇数个数
            int even = 0;//偶数个数
            for (int i= 0;i

该题参考下面链接 

全网最详细第十四届蓝桥杯JAVA B组省赛真题讲解（上）_哔哩哔哩_bilibili