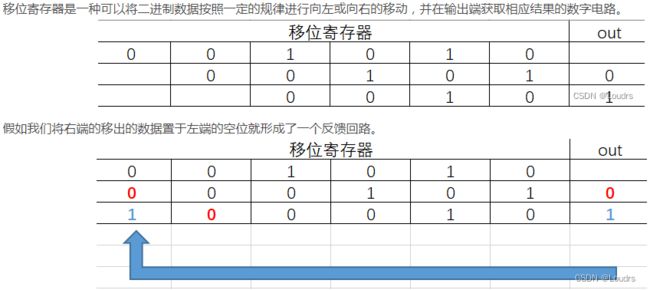
【业务领域】Scramble/de-Scramble加扰解扰总结

一、加扰/解扰是什么

什么是加扰（scrambler)?

所谓加扰是将源数据流与一个随机序列异或后，再发送出去，异或操作完成后的数据流基本是伪随机的。所谓加扰技术，就是不用增加多余度而扰乱信号，改变数字信号统计特性，使其近似于白噪声统计特性的一种技术。

异或使用的随机序列是如何产生的？

以PCIE 为例，PCIE总线通过一个16位线性反馈移位寄存器(Linear Feedback Shift register, LFSR),产生为随机序列，该移位寄存器的表达式如下所示：

G(x)=X¹⁶+X⁵+X⁴+X³+1

该公式是一个本原多项式（具有最大周期的不可以约多项式，详细见此文章《高等代数：有理数域上的不可约多项式》），使用该公式可以产生一个周期为216-1的伪随机序列。对应的，由本预案多项式作为生成多项式所产生的LFST序列为最大周期序列。这些序列一般被称为m-序列，在m-序列中“0”和“1”所占的比例相对均衡，但是1的个数比0的个数多1，因为全0不能作为初始值，，也不可能是中间状态。

源数据流与这个伪随机序列中的字符流进行异或操作，从而称为一个相对较为随机的字符流，从而降低了数据流的EMI噪声。

什么是解扰（de-scrambler)?

PCIE数据发送端有加扰，数据接收端也有解扰操作，解扰与加扰使用相同的公式，必须完全同步，即LFSR使用相同的初始值。在PCIE链路的两端，该初始值为0xFFFF。PCIE链路两端设计每次加解扰一个8b数据后，LFSR进行8次移位操作。

二、为什么需要加扰/解扰

一般来说，数字通信系统的设计及其性能都与所传输的数字信号的统计特性有关。在数字通信设备中，通常从0和1码的交变点提取位定时信息，若经常出现长0或1游程，则将影响位同步的建立和保持。如果数字信号具有周期性，则信号频谱中存在离散谱线。为了限制这种串扰，常要求数字信号的最小周期足够长。在serdes高速链路中，为了提高链路的鲁棒性，应该尽量避免长0，长1以及周期性数据的出现。

通过“加扰”的方法消减EMI噪声，所谓加扰是将源数据流与一个随机序列异或后，再发送出去。此时被发出的数据流也基本是伪随机的，从而降低了发送数据时产生的EMI噪声。

如果我们能够先将信源产生的数字信号变换成具有近似白噪声统计特性的数字序列，再进行传输，这样就可以给数字通信系统的设计和性能估计带来很大方便。

这种技术的基础是建立在反馈移存器序列（伪随机序列）的理论基础之上。

扰码有以下两个作用：

(1)扰码可以使重复的数据图案的频谱被展宽。例如，在数据流中重复出现序列10101010，这会导致高频离散频谱的出现从而产生较强的EMI(电磁干扰）。当进行扰码后，该数据被随机化，EMI噪声会大大减弱。

(2)扰码的另一用处是减少并行线路中的串扰。扰码可以使功率谱分布更为平滑和均匀，从而降低高频串扰。

在串行总线为了实现一下三中目的的通常会使用加扰技术：

1：序列均衡：要求序列不能出现长0或者1，面向时钟嵌入的总线可以保证时钟恢复避免失步；减少直流分量更好的实现交流耦合；

2：序列随机化：避免传输信号具有周期性。在多路传输中造成串扰；

3：在通信领域加扰技术可以实现加密，扩频，划分频道等应用

通俗解释：加扰是数字信号的加工处理方法，就是用扰码与原始信号相乘，从而得到新的信号，与原始信号相比，新的信号在时间上，频率上被打散，因此，从广义上说，加扰也是一种调制技术，加扰也有一个你操作，就是解扰。

三、怎么实现加扰/解扰

1、数学基础

1.1 逻辑异或

异或运算使用符号⊕或者nor表示，真值表如下
F = A ⊕ B

A B F
0 0 0
0 1 1
1 0 1
1 1 0
异或运算可以有3种理解方式：

1 相同得0，不同得1
2 二进制加法，只留模2的余数，抛弃进位（模2加法）
3 二进制减法，大数减小数，不借位（模2减法）

1.2 模2乘法 和 模2除法
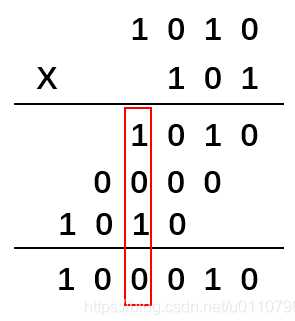
两个二进制数的模2乘法是指在乘法竖式运算中需要做加法的地方都使用异或运算。

模2乘法1010 * 101=100010，下图红框中，1⊕0⊕1=0，没有进位：

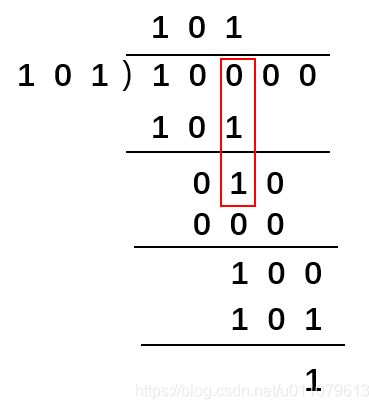
两个二进制数的模2除法是指在除法竖式运算中需要做减法的地方都使用异或运算。

模2除法10000 / 101=101余1，下图红框中，0⊕1=1，没有借位：

2、线性反馈移位寄存器

反馈移位寄存器的工作原理是什么呢？

反馈移位寄存器（Feedback Shift Register，FSR）：每个时钟脉冲，移位寄存器向右移动一位，则移位寄存器的左左侧就会空出一位。这个如果左侧有输入，则移位寄存器的右侧输出端则会有源源不断的数据输出。如果来自移位寄存器的某些序列根据一定的反馈函数形成左侧输入，则称该结构为反馈移位寄存器。当反馈移位寄存器的反馈函数f(x)是线性时，则称为线性反馈移位寄存器。线性反馈移位寄存器的反馈函数为：对移位寄存器中的某些位进行异或。将反馈函数得到的计算结果反馈到移位寄存器的最左边，即得到了线性反馈移位寄存器。

在现代密码学中存在一种特殊移位寄存器——线性反馈移位寄存器（Feedback Shift Register，FSR）。

线性反馈移位寄存器由N级触发器和若干异或门组成，事先选定初始值即随机种子(seed)和抽头（参与运算的比特位），再在种子的基础和抽头的运算下得到一组人工生成的伪随机序列。之所以是伪随机序列，是因为该随机数是按照一定算法模拟产生的，其结果是确定的并且可预见的，因此并不是真正的随机数。对于LFSR随机种子和抽头的选择就十分重要，如果随机种子和抽头发生改变，线性反馈移位寄存器LFSR产生的随机数也会相应改变。

除了知道LFSR的工作原理，应当还了解一些重要的基本概念：

如图所示，这是一个三级反馈移位寄存器，此时选择种子即初始值001可以遍布除000外的所有状态，此时LFSR级数为3且周期为7。

线性反馈移位寄存器： (Linear Feedback Shift Register，LFSR)和循环冗余码（Cyclic Redundancy Check，CRC）是微控制器中常用的底层原理。LFSR用于生成伪随机数，后者用于生成检错码。他们的数学原理都是一样的。

LFSR通常由移位寄存器和异或门逻辑组成。

原理：扰码器使用LFSR实现，用来产生伪随机比特序列，它和串行输入的数据进行异或，从而实现对输入数据的随机化。正如我们在LFSR部分讨论过的，伪随机序列也是周期重复的，其周期长度取决于LFSR中触发器的级数和所选择的多项式。接收电路本地有一个和发送电路中相同的伪随机序列产生器，它产生的数据与接收数据进行异或，可以恢复出发端原始的串行数据。

这里用到了一个逻辑运算表达式：如果A^B=C，那么C^B=A，此处A为原始数据，B为扰码器的输出，C为扰码后的数据。如图6.4所示：

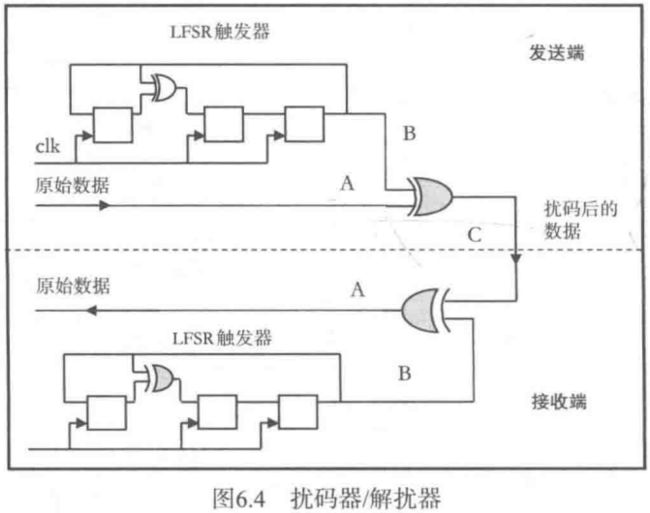
在实际应用中，加扰技术一般采用两种典型的方式：

（1）帧同步码（Frame synchronous Scrambling，FSS）

（2）自同步扰码（Self synchronous Scambling，SSS）

帧同步扰码结构是由反馈移位寄存器构成的，由反馈移位寄存器产生伪随机序列再通过异或单元实现扰码和信号的逻辑加，帧同步加扰器的主要参数是伪随机序列生成式和移位寄存器的初始状态，其中生成式决定反馈移位寄存器的结构，此部分收发双方可以事先约定，但移位寄存器的初始状态也称为“扰码seed”是需要收发双方采用某种方式完成交互的，比如在收到某个特定值时设定某个固定初始化状态。

上述说明可以看到，帧同步扰码的伪随机序列的生成与输入信号无关，具有良好的随机化性能，但是在使用中收发双方需要同步完成初始化设定才能实现解扰，而自同步扰码无需通过帧同步实现移位寄存器的初始化同步，可以在正常通讯中完成同步，自扰码同步原理比较简单，自同步的伪随机序列生成与输入信号是相关的，当输入信号持续输入一段时间后，扰码器和解码器的寄存器值就会变成一致，也就完成了同步，之后就可以确定的完成解扰，一般自同步过程都是在协议中空闲状态完成。

帧同步扰码和自同步扰码在最坏情况下都无法产生随机序列，帧同步扰码可以实现错误检测，发送中的错误不会产生扩散，但是需要确保初始化种子同步否则会产生连续错误；自同步扰码不需要额外的同步机制，但是在扰码端输入单比特错误会导致输出端的多位错误，错误数与加扰器反馈抽头相关。

扰码技术所表现出的特性都是与生成的伪随机序列的特性相关的，而在逻辑电路中主要采用线性反馈移位寄存器来生成伪随机序列，而某种生成式能产生多大周期的伪随机序列？什么生成式能产生最大生成序列，生成M序列的特性？这些都是扰码技术需要的数学支撑，在实际应用中可以直接按照协议规范中生成式来实现扰码或者解码，可以不用来哦姐相关知识。

串行扰码解码逻辑实现是比较简单的，通过生成式画出逻辑电路图，直接通过图形或者是硬件描述语言实现就可以，随着串行总线速度的提升，例如PCIE，通过串行移位的方式来计算扰码已经很难满足高速需求，所以提出了并行扰码技术，实际上也是把多次串行移位的结果一次性写出，多位串行迭代的逻辑经过简化就可以得到并行实现的逻辑。

抽头和特征多项式是什么

f(Rn-1, … R1, R0) = (Rn-1gn)⊕(Rn-2gn-1)⊕…⊕(R0*g1)*g0 可以用多项式表示为：

G(x)=gnxn+gn-1xn-1+…+g1x+g0

G(x)称为LFSR的特征多项式。

影响线性反馈寄存器下一个状态的 gi = 0 或1叫做抽头，抽头的设定会决定线性反馈寄存器存储的结果 (Rn-1, … R1, R0) 的变化规律。

通常N位的线性反馈寄存器最多有 2’N 个不同的状态。但是如果出现初值为N个0的情况，线性反馈寄存器陷入死循环，要排除掉。所以N位线性反馈寄存器能产生最长的不重复序列为 2’N-1。

抽头的位置会影响LSFR的最大输出状态的个数
例如：3位的抽头为(g3, g2, g1, g0) = (1, 1, 0, 1)会产生7个状态（多项式对应为：G(x)=x3+x2+1)
若抽头为(g3, g2, g1, g0) = (1, 0, 1, 1)，会产生2个状态（多项式对应为：x3+x+1)。

使最大输出序列长度为2N-1的不可约多项式称为LFSR的本原多项式，本原多项式产生的寄存器序列为M序列。

当N位下，本原多项式不是唯一的。下表为不同的位下的本原多项式：

阶线性反馈移位寄存器实例:

上图为3阶线性反馈移位寄存器：
抽头为(g3, g2, g1, g0) = (1, 1, 0, 1)
多项式对应为：G(x)=x3+x2+1
线性反馈函数R0 = f(R2, R1, R0) = R1⊕R2
初始值为SEED = (R2, R1, R0) = (1, 0, 1)

3阶线性反馈移位寄存器周期为7：

通过设定seed和抽头，LFSR最多可产生2N-1个序列，这些序列之间看似是随机产生的，之所以称之为伪随机，是因为这些数是通过具体的关系式产生，最终会实现循环。

抽头(tap)：影响线性反馈寄存器下一个状态的比特位叫做抽头，抽头的设定会决定线性反馈寄存器最大的输出序列长度，抽头通常用有限域算数中模2的多项式来表示（例如模2的多项式为：x8+x6+x4+1）。

通常N bits的线性反馈寄存器能产生最长的不重复序列为2N-1。因为当所有寄存器的输出为全零状态时，线性反馈寄存器陷入死循环，故Nbit的线性反馈寄存器的输出状态有2N-1。
抽头的位置会影响LSFR的最大输出状态的个数,例如：3bit的抽头为【3,2】会产生7个状态（多项式对应为：x3+x2+1)，若抽头为【3,1】会产生2个状态（多项式对应为：x3+x+1)。

当N bits下，抽头的设定产生的最大输出序列长度为2N-1时，此时对应的模2多项式为本原多项式，能达到最长序列的多项式不是唯一的。下表为不同的bits下，抽头的设定（对应不同的本原多项式）和最大的输出状态个数关系表。

上面提到N bits的LFSR能产生最大输出状态的个数为2N-1，N越大，随机性就越大。如果输出状态包括全零的状态，最大输出状态的个数可达到2N，那么通过对LFSR做如下图的修改，即如果检测到Q[7]-Q[0]输出状态为全零时，经过~|Q[6:0]^Q[7]逻辑运算后输出的结果为1，进而保证线性反馈寄存器不会陷入死循环中，此处的死循环意思是指输出状态总保持全0或者全1，LFSR本身是可以无限循环的。需要说明的是，最后一位必须参与反馈。与此同时，对于斐波那契线性反馈移位寄存器，若采用异或反馈，全0为非法状态，若采用同或反馈，全1为非法状态，不管是斐波那契还是伽罗瓦TFSR，为避免非法，种子可选取全1或全0之外的组合。

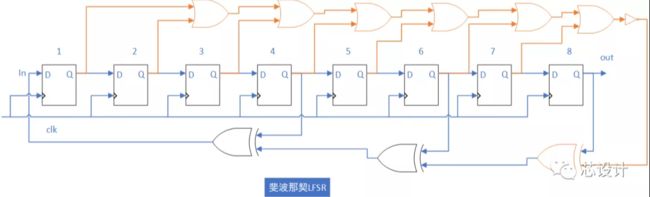
在实际的应用中，例如crc的校验，会用到模2的多项式的运算，遵循如下的计算原则：

LFSR有哪些分类呢？

主要有两种类型的LFSR（多到一，一到多）。对于多到一类型，多个触发器输出进行异或运算，输出结果进入一个寄存器，对于一到多类型，一个触发器的输出进入异或函数，计算结果驱动多个触发器

1.斐波那契LFSR：多到一型LFSR(many to one)
斐波那契LFSR：抽头序列对应bit位置的多个寄存器的输出异或后驱动一个寄存器输入。

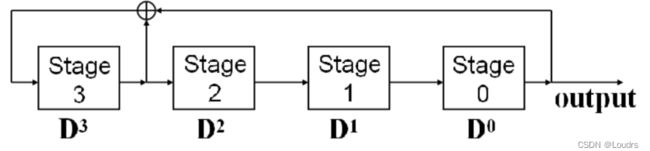
以斐波那契(外部LFSR)为例，有n个二进制寄存器R0-Rn-1，每个寄存器值为0或1。


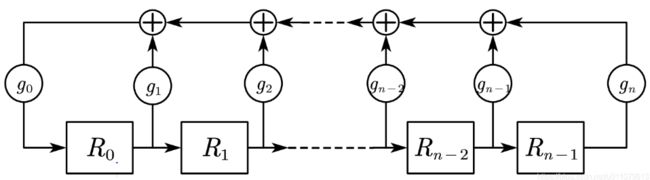
2.伽罗瓦LFSR：一到多型LFSR(one to many)
伽罗瓦LFSR：最后一个寄存器的输出通过与抽头序列对应位置寄存器前一级寄存器的输出异或后驱动多个抽头序列对应位置的寄存器。

线性反馈移位寄存器(LFSR)主要包括两大类：斐波那契(外部LFSR),又称many-to-one；伽罗瓦(内部LFSR),又称one-to-many。

如下图(模2的多项式：x8 + x6+x4+1)：

斐波那契LFSR与伽罗瓦LFSR有哪些差异呢？

LFSR计数器具有速度快，消耗逻辑门少的特点。
伽罗瓦LFSR具有更高的速度，因为两个触发器之间只有一个异或门。
斐波那契LFSR在首尾两个寄存器之间有多个异或门，组合逻辑延时更大，因为为了满足建立保持时间的要求，其频率更小（周期更大），速度更慢。

Tips：

种子的选择十分重要，种子初始值一定不能为全0；
抽头的设计也十分重要，抽头设计时尽量使LFSR达到最大周期；
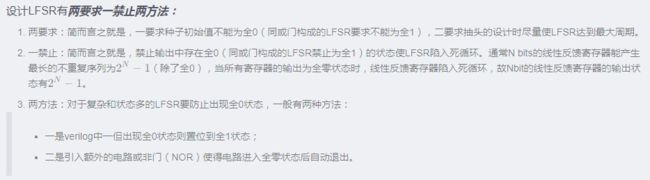
通常N bits的线性反馈寄存器能产生最长的不重复序列为2^N − 1。因为当所有寄存器的输出为全零状态时，线性反馈寄存器陷入死循环，故Nbit的线性反馈寄存器的输出状态有2^N−1。
一定要防止出现全0状态，一般有两种方法：一是verilog中一但出现全0状态则置位到全1状态；二是引入额外的电路或非门（NOR）使得电路进入全零状态后自动退出。（有兴趣的可以查阅相关资料，此处不展开细说。）

参考来源

LFSR应用场景是什么呢？

LFSR广泛应用在：伪随机数，伪噪声序列，计数器，BIST，CRC校验，伪随机数生成、伪噪声序列生成、计数器、数据的加密、扰码器/解码器、信号生成和测试等领域，是一种非常有用的数字电路设计技术。
下面对其中的一些典型应用进行介绍。

• 伪随机序列发生器：LFSR 可以按比特位顺序产生一个周期性序列，并通过适当的反馈多项式来调节其生成的序列，可作为数字化通信中的伪随机序列发生器使用。
• LFSR计数器：LFSR可用于构建通过随机序列状态进行计数的计数器。 与常见的计数器相比， LFSR计数器具有速度快 、 消耗逻辑门少的特点。
• 数据的加密和CRC校验：在通信系统中使用 CRC 校验时通常需要使用一个预定义的 LFSR 系列和特定的反馈多项式来计算校验码。这种结构可以有效地检测数据传输过程中发生的错误，保证数据的完整性和正确性，提高系统的可靠性与稳定性。循环冗余码（Cyclic Redundancy Check，CRC）是微控制器中常用的底层原理。LFSR用于生成伪随机数，后者用于生成检错码。他们的数学原理都是一样的。
• 扰码器/解扰器 ：用户数据发送前和扰码器生成的序列进行异或然后发出，此时发送的数据就是经过扰码的数据。 接收电路与发送电路采用相同的多项式，解扰器就可以将发送端原始的用户数据恢复出来。

伪随机数 ：前面已经提到，LFSR最多可产生2N-1个序列，这些序列之间看似是随机产生的，之所以称之为伪随机，是因为这些数是通过具体的关系式产生，而非像random()这样产生真正的随机数，且最终会实现循环。

伪噪声序列用于扰码和解码：
异或使用的随机序列是如何产生的？
以PCIE 为例，PCIE总线通过一个16位线性反馈移位寄存器(Linear Feedback Shift register, LFSR),产生为随机序列，该移位寄存器的表达式如下所示：
G(x)=X16+X5+X4+X3+1
该公式是一个本原多项式（具有最大周期的不可以约多项式），使用该公式可以产生一个周期为216-1的伪随机序列。对应的，由本预案多项式作为生成多项式所产生的LFST序列为最大周期序列。这些序列一般被称为m-序列，在m-序列中“0”和“1”所占的比例相对均衡，但是1的个数比0的个数多1，因为全0不能作为初始值，，也不可能是中间状态。
源数据流与这个伪随机序列中的字符流进行异或操作，从而称为一个相对较为随机的字符流，从而降低了数据流的EMI噪声。

LFSR计数器：
优点：传统的二进制计数器用复杂的或大扇入逻辑产生进位信号，LFSR以牺牲二进制计数序列为代价，用相当简单的结构与逻辑实现很高的速度(逻辑资源少，速度高)，这种移位寄存器又称为伪随机序列发生器；LFSR计数器的计数序列就是伪随机序列，
缺点：LFSR的缺点是本原形式必须初始化为有效状态，计数序列不是通常的递增或递减，这样就不易预测，而且某些场合二进制计数器更加适用。

3、扰码器的分类

3.1 串行扰码器

结合LFSR及其给出的多项式可以方便地设计串行扰码器。对于串行扰码器，一个时钟周期只有1比特的用户数据到达，每个时钟上升沿之后输出一位经过扰码后的数据，同时LFSR内部触发器的值被更新。然而，很多时候在一个时钟周期内到达多个比特的数据，此时我们需要设计并行扰码器，它可以在一个时钟周期内输入和输出多位数据。

3.2 并行扰码器

对并行数据加扰，遵循和串行加扰同样的算法。以每个时钟周期到达8位并行数据为例，LFSR伪随机序列产生器需要在每个时钟周期内产生8位随机数，同时扰码器在每个时钟周期内产生8位扰码后的随机数据。我们可以假定有一个8倍于当前并行数据工作时钟的虚拟时钟，在8个虚拟时钟周期之后，LFSR伪随机序列产生器可以产生8位数据（注意，LFSR伪随机序列产生器的输出与当前输入数据是无关的，与寄存器的当前状态有关），这8位数据与输入的8位原始数据进行异或，就可以得到并行扰码的最终结果。在后面的部分中，我们将对PCIe专用扰码器的实现进行讨论。并行扰码技术同样适用于16比特或32比特的并行数据。

下面这个网站直接生成加扰代码
OutputLogic.com

4、扰码电路设计要点

我们讨论了如何对串行数据及并行数据进行加扰处理，然而，为了实现扰码电路，还需要注意以下三个要点。

(1)扰码器初始化

发送电路和接收电路必须可以独立地对扰码器和解扰器进行初始化，否则二者就不能实现同步，从而接收电路也无法恢复出原始数据。PCIe中使用了一个名为COM的字符，发送电路和接收电路都可以识別该字符，并在收到该字符后将电路中的扰码器置为预先约定的相同的初始始值。这些COM字符被周期性地发送，使得收发双方能够同步或者对LFSR进行周期性的初始化。

(2)扰码器暂停

正常工作时，LFSR内部触发器的值在每个时钟周期都会进行更新，然而，LFSR应该可以被暂停更新。例如，在PCIe中，数据流中会添加或删除SKIP字符，并且SKIP字符的数量在中间处理过程中还可能发生变化。无论是发送电路还是接收电路，SKIP字符都是不需要进行扰码和解扰处理的，因此扰码电路和解扰电路应该可以在这些字符出现时进入“暂停”状态，“跳过”对它们的处理。

(3)扰码器去使能

扰码器还应该可以工作在LFSR内部寄存器不断更新，但不产生有效输出的状态。例如，在PCIe中，训练字符(TS1/TS2)未被加扰，但LFSR内部仍能不断更新。

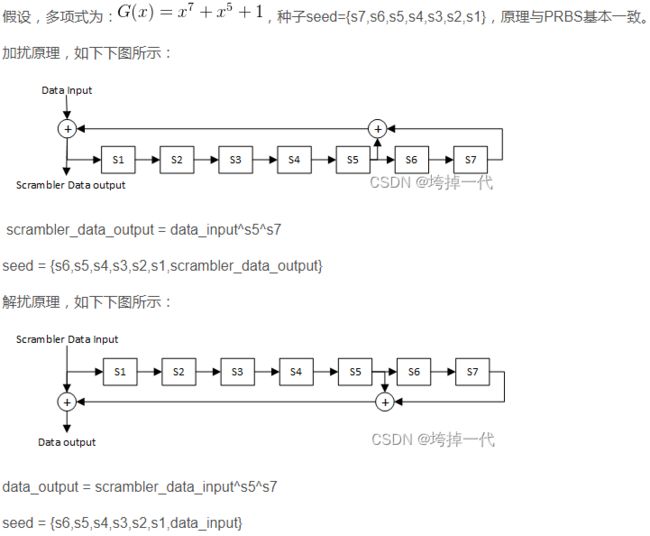
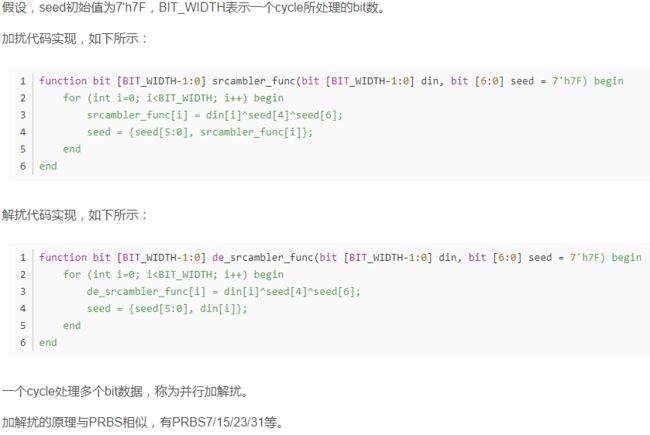
4)初始值是怎么使用的？
不同LFSR的初始值可能不同，往往需要在某些特殊码型到来时赋值为初始值。

5、有没有更优的办法实现加扰：

----待更新；

四、各类协议对加扰解扰的要求

PCIE协议中加扰解扰

scramble通过LFSR(Linear Feedback Shift Register)来实现。

对于2.5gbps/5.0gbps，在发送端，数据先scramble，然后在进行8b/10b编码；在接收端，数据先进行8b/10b解码，然后再de-scramble。scramble LFSR的多项式是：G(X)=X^16 + X^5 + X4 + X^3 + 1

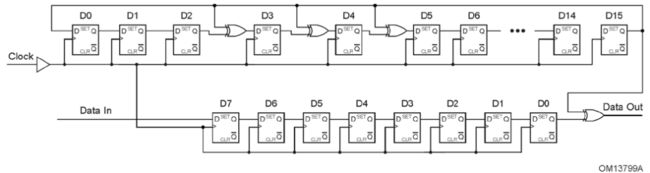
PCIe扰码器(如图6.5所示）是一个16位LFSR多项式如下：

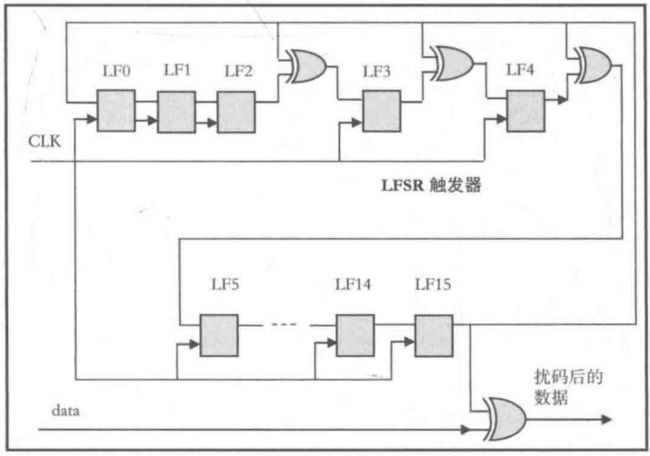
它有16个LFSR触发器，图6.5是其具体电路;

COM字符将LFSR初始化为16’hFFFF;

SKP字符可以令其工作暂停。

PCIe扰码器工作波形如图6.6所示。

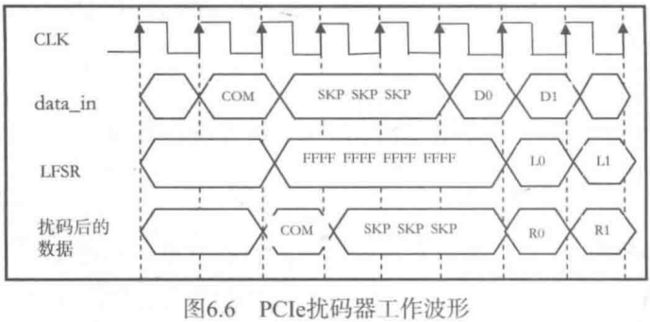
scramble规则：

1. COM symbol初始化LFSR

2. LFSR value is advanced eight serial shifts for each symbol except SKP

3. 除OS外的所有数据symbol（D码），Compliance Pattern， Modified Compliance Pattern都要scamble。

4. 所有的K码不需要scramble。

5. LFSR的初始seed是FFFF。当COM字节从Transmit LFSR发出后，LFSR立即被初始化；每当COM进入Receive LFSR，接收端的LFSR立即初始化。

6. Scramble只能在Configuration状态结束时disable。

7. Scramble不应用在loopback slave。

8. scramble在Detect状态时总是默认enabled.

对于8Gbps：

LFSR多项式：G(X) = X^23 + X^21 + X^16 + X^8 + X^5 + X^2 + 1

Scramble规则：

1. 2bit的sync header不用scramble，也不advance LFSR。

2. EIEOS的所有16symbol都跳过scramble，在发送完EIEOS的最后一个symbol后，将scramble LFSR初始化，在收到EIEOS最后一个symbol后，将descramble LFSR初始化。

3. TS1/TS2的symbol 0跳过scramble, symbol 1-13需要scramble，symbol 14/15在需要DC Balance时跳过scramble，否则进行scramble。

4. FTS的所有16个symbol都不用scramble

5. SDS的所有16个symbol都不用scramble

6. EIOS的所有16个symbol不用scramble

7. SKP的所有symbol都不用scramble

8. 发送所有的OS（SKP除外）symbol时都会advance LFSR，对于SKP的所有symbol，LFSR都不会advance。

9. 接收端通过OS的symbol 0来决定是否要advance LFSR，如果symbol 0时SKP，LFSR在这个block都不用advance，否则LFSR在这个block都需要advance

10. Data block的所有16 symbol都会scramble，并advance LFSR。

11. symbol scramble的顺序是，从低位到高位。

12. LFSR seed与在进入Configuration.Idle后分配的Lane number有关，各条Lane不一样。

13. 使用128b/130b时，不能再Configuration.Complete状态中disable Scramble。

14. Loop back slave不要descramble或scramble loop-back bit stream。

PS：此规则仅供参考，具体规则以PCIE协议为准；

PCIe2.5\5G速率扰码器 - Verilog RTL
// note ： 每时钟周期处理8比特并行数据

module scrambler_8bits
 (clk,
 rstb,
 data_in,
 k_in,
 disab_scram,
 data_out,
 k_out);

//****************************************************************
input clk;
input rstb;
input [7:0]data_in; // input data to be scrambled
input k_in; // when 1, the input is a control character.
// when 0, the data is regular data

input disab_scram; // when 1 scrambling is disabled ,
output [7:0] data_out; // scrambled data output
output k_out; // when 1 the output is a control character.

//****************************************************************
localparam LFSR INIT = 16‘hFFFF;

reg  [15:0] lfsr, lfsr_nxt;
wire [15:0] lfsr_int;
wire initialize_scrambler, pause_scrambler;
reg  [7:0] data_out, data_out_nxt;
wire [7:0] data_out_int;


/* First find the equations for the LFSR flops. Since there are 8 bits of data coming input, the LFSR flops value moves 8 times (as there is an imaginary clock running 8 times faster). Find the intermediate value. Refer to PCIe sepe for the following algorithm */

assign lfsr_int[0]  = lfsr[8];
assign lfsr_int[l]  = lfsr[9];
assign Ifsr_int[2]  = lfsr[10];
assign lfsr_int[3]  = lfsr[8] ^ lfsr[ll];
assign lfsr_int[4]  = lfsr[8] ^ lfsr[9]  ^ lfsr[12];
assign lfsr_int[51  = lfsr[8] ^ lfsr[9]  ^ lfer[10] ^ lfsr[13];
assign lfsr_int[6]  = lfsr|9] ^ lfsr[10] ^ lfsr[l1] ^ lfsr[14];
assign lfsr_int[7]  = lfsr[10]^ lfsr[ll] ^ lfsr[12] ^ lfsr[15];
assign lfsr_inr[8]  = lfsr[0] ^ lfsr[l1] ^ lfsr[12] ^ lfsr[13];
assign lfsr_int[9]  = lfsr[l] ^ lfsr[12] ^ lfsr[13] ^ lfsr|14];
assign lfsr_int[10] = lfsr|2] ^ lfsr|13] ^ lfsr[14] ^ lfsr[15];
assign lfsr_int[l1] = lfsr[3] ^ lfsr[l4] ^ lfsr[15];
assign lfsr_int[l2] = lfsr[4] ^  lfsr[15];
assign lfsr_int[13] = lfsr[5];
assign lfsr_int[14] = lfsr[6];
assign lfsr_int[15] = lfsr[7];

// now use the special handles to define lfsr_nxt[15:0]
//****************************************************************
assign initialize_scrambler = (data_in == 8'hBC) && (k_in == 1); //COM char
assign pause_scrambler = (data_in == 8'h1C) && (k_in == 1) // SKP char
always @(*)
   begin
       lfsr_nxt = lfsr;
   if (disab_scram | pause_scrambler )
       lfsr_nxt = lfsr;
   else if (initialize_scrambler)
       lfsr_nxt = LFSR_INIT;
   else
       lfsr_nxt = lfsr_int;
   end
   
   
   // flop inference
   
always @(posedge clk or negedge rstb)
   begin
     if(!rstb)
       lfsr <= LFSR_INIT;
      else
       lfsr <= lfsr_nxt;
   end
// Now we need to perform the XOR operation with the input data_in to derive
// scrambled data First derive data_outjnt[7:0]
//****************************************************************
assign data_out_int[0] = data_in[0] ^ lfsr[l5];
assign data_out_int[1] = data_in[1] ^ lfsr[l4];
assign data_out_int[2] = data_in[2] ^ lfsr[13];
assign data_out_int[3] = data_in[3] ^ lfsr[12];
assign data_out_int[4] = data_in[4] ^ lfsr[l1];
assign data_out_int[5] = data_in[5] ^ lfsr[l0];
assign data_out_int[6| = data_in[6] ^ lfsr[9];
assign data_out_int[7] = data_in[7] ^ lfsr[8];

always @(*)
begin
 data_out_nxt = data_out_int;
 
 if (disab_scram || k_in) // scrambling disabled or input control character
       data_out_nxt = data_in;
 else
       data_out_nxt = data_out_int;
end

// flop inference
//****************************************************************
always @(posedge clk or negedge rstb)
begin
 if(!rstb)
     data_out <= 'd0;
 else
     data_out <= data_out_nxt;
end
endmodule

五、其他总结

CRC计算的在线网站

http://www.ip33.com/crc.html

---

致谢：
本文仅用于学习用途，无任何商用，部分材料整理来源网络，特此感谢 ，如有侵权，告知删除；

参考资料：
LFSR(斐波那契大战伽罗瓦)
PCIE中的加扰与解扰
总线技术：加扰
pcie 中的scramber 和 de-scramber 技术
加解扰原理
scramble